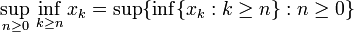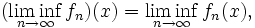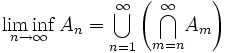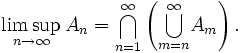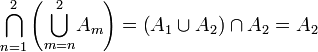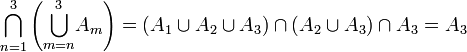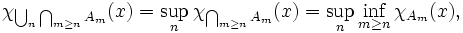- Limes superior
-
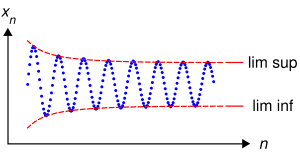
In der Mathematik bezeichnen Limes superior und Limes inferior einer Folge (xn) den größten bzw. kleinsten Grenzwert konvergenter Teilfolgen von (xn). Analog werden Limes superior und Limes inferior von reellwertigen Funktionen definiert. Limes superior und Limes inferior sind ein partieller Ersatz für den Grenzwert, falls dieser nicht existiert.
Inhaltsverzeichnis
Formale Definition
Formal wird der Limes inferior einer Folge (xn) definiert als
bzw. als
und mit
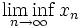 oder auch mit
oder auch mit 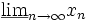 bezeichnet.
bezeichnet.
Diese Definitionen sind in einer partiell geordneten Menge sinnvoll, falls die vorkommenden Suprema und Infima existieren. In einem vollständigen Verband existieren diese Größen immer, so dass in diesem Fall auch jede Folge einen Limes inferior und einen Limes superior besitzt.Existieren Limes inferior und Limes superior einer Folge (xn), so ist
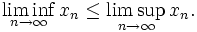
Folgen reeller Zahlen
Für eine Folge reeller Zahlen müssen Limes inferior und Limes superior nicht existieren, da die reellen Zahlen keinen vollständigen Verband bilden. Wenn sie existieren, sind sie der kleinste bzw. der größte Häufungspunkt der Folge. Häufig werden Limes inferior und Limes superior allerdings als Elemente der erweiterten reellen Zahlen
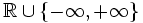 betrachtet; in diesem Fall existieren sie immer.
betrachtet; in diesem Fall existieren sie immer.Für eine Folge von reellen Funktionen
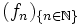 mit
mit 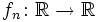 für
für 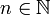 sind Limes inferior und Limes superior punktweise definiert, d.h.
sind Limes inferior und Limes superior punktweise definiert, d.h.analog für lim sup.
Eine der bekanntesten mathematischen Aussagen, die den Begriff des Limes inferior verwenden, ist das Lemma von Fatou.
Folgen von Mengen
Limes superior und Limes inferior
Für eine beliebige Menge Ω bildet die Potenzmenge P(Ω) einen vollständigen Verband unter der durch die Teilmengenrelation definierten Ordnung. Der Limes inferior einer Folge (An) von beliebigen Teilmengen von Ω ist die Menge aller Elemente aus Ω, die in fast allen An liegen. Der Limes superior der Mengenfolge (An) ist die Menge aller Elemente aus Ω, die in unendlich vielen An liegen.
In der Sprache der Mengenlehre ausgedrückt,
und
Der Limes superior von Mengen wird beispielsweise im Borel-Cantelli-Lemma verwendet.
Man kann sich die Formeln klar machen, wenn man zunächst Schnitt beziehungsweise Vereinigung endlicher Mengen betrachtet. Die rechte Seite der Gleichung für den Limes superior für n = 2 und n = 3 lautet
In jedem Schritt wird eine weitere Menge aus der Vereinigung aller Mengen herausgeteilt. Zurück bleibt schließlich für alle endlichen n nur An. Im unendlichen bleiben nur Mengen übrig, die in unendlich vielen An vorkommen, weil diese niemals herausgeteilt werden können. Somit ist der Limes superior gerade der Teil, der in unendlich vielen An liegt.
Zusammenhang mit Folgen von Zahlen
Die charakteristische Funktion des Limes inferior bzw. Limes superior von Mengen ist der punktweise Limes inferior bzw. Limes superior der charakteristischen Funktionen der einzelnen Mengen: Aus
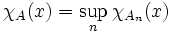 für
für 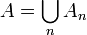
und
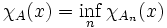 für
für 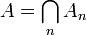
folgt
analog für lim sup.
Konvergenz
Man sagt, die Folge (An) konvergiert gegen eine Menge A, falls der Limes inferior und der Limes superior gleich sind und schreibt
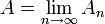 oder auch
oder auch 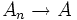 . Eine Folge von Teilmengen einer Menge X konvergiert genau dann, wenn es zu jedem x einen Index N gibt, so dass entweder
. Eine Folge von Teilmengen einer Menge X konvergiert genau dann, wenn es zu jedem x einen Index N gibt, so dass entweder 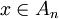 für alle
für alle 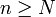 oder
oder 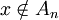 für alle
für alle 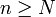 gilt.
gilt.Monotone Konvergenz
Ist
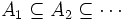 , dann kann man zeigen, dass (An) gegen eine Menge A konvergiert und man schreibt
, dann kann man zeigen, dass (An) gegen eine Menge A konvergiert und man schreibt 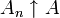 .
.Entsprechend kann man für
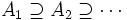 zeigen, dass (An) gegen eine Menge A konvergiert und man schreibt
zeigen, dass (An) gegen eine Menge A konvergiert und man schreibt 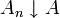 .
.Limes superior und Limes inferior von Funktionen
Ist eine reellwertige Funktion
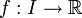 auf einem Intervall I gegeben und ξ ein innerer Punkt des Intervalls, so sind Limes superior und Limes inferior jene Werte aus den erweiterten reellen Zahlen
auf einem Intervall I gegeben und ξ ein innerer Punkt des Intervalls, so sind Limes superior und Limes inferior jene Werte aus den erweiterten reellen Zahlen 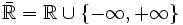 , die folgendermaßen definiert sind:[1]
, die folgendermaßen definiert sind:[1]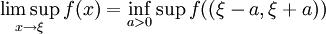 ,
,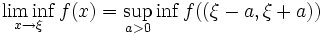 .
.
f((ξ − a,ξ + a)) bezeichnet dabei die Bildmenge des offenen Intervalls (ξ − a,ξ + a); a ist dabei so klein zu wählen, dass
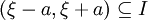 .
.Analog zu einseitigen Grenzwerten werden ein einseitiger Limes superior und ein einseitiger Limes inferior definiert:
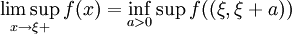 ,
,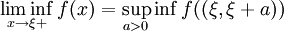 ,
,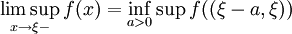 ,
,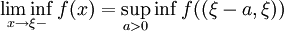 .
.
Limes superior und Limes inferior von Funktionen werden beispielsweise bei der Definition der Halbstetigkeit verwendet.
Quellen
- ↑ Nelson Dunford and Jacob T. Schwartz. Linear Operators. Part I. General Theory. John Wiles and Sons, 1988, p. 4. ISBN 0-471-60848-3.
Literatur
- Heinz Bauer: Maß- und Integrationstheorie. 2. Auflage, De Gruyter, Berlin 1992, ISBN 3-11-013626-0 (Gebunden), ISBN 3-11-013625-2 (Broschiert), S. 93 (zu Folgen von Mengen).
Wikimedia Foundation.