Liste der Quantengatter

Dies ist eine Auflistung verschiedener Quantengatter und deren Funktion.

Quantengatter mit einem Eingang

Quantengatter, die sich auf einzelne Quantenbits beziehen

Symbol und Funktion1	Bezeichnung	Funktion	Beschreibung
	Identität	$\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$	Identität des hyperkomplexen Eingangs und daher keine Veränderung am Quantenzustand
	Pauli-X-Gatter Nicht-Gatter	$\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}$	Spiegelung des hyperkomplexen Eingangs an der X-Achse
	Pauli-Y-Gatter	$\begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix}$	Spiegelung des hyperkomplexen Eingangs an der Y-Achse
	Pauli-Z-Gatter	$\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$	Spiegelung des hyperkomplexen Eingangs an der Z-Achse
	Hadamard-Gatter	$\frac{1}{\sqrt{2}} \cdot \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}$
	X-Rotationsgatter	$\frac{1}{\sqrt{2}} \cdot \begin{pmatrix} 1 & i \\ i & 1 \end{pmatrix}$	Dreht den komplexen Eingang 90° (π/2) um die X-Achse
	Y-Rotationsgatter	$\frac{1}{\sqrt{2}} \cdot \begin{pmatrix} 1 & 1 \\ -1 & 1 \end{pmatrix}$	Dreht den hyperkomplexen Eingang 90° (π/2) um die Y-Achse
	(-X)-Rotationsgatter	$\frac{1}{\sqrt{2}} \cdot \begin{pmatrix} 1 & -i \\ -i & 1 \end{pmatrix}$	Dreht den komplexen Eingang -90° (-π/2) um die X-Achse
	(-Y)-Rotationsgatter	$\frac{1}{\sqrt{2}} \cdot \begin{pmatrix} 1 & -1 \\ 1 & 1 \end{pmatrix}$	Dreht den hyperkomplexen Eingang -90° (-π/2) um die Y-Achse
	T-Gatter4 Phasen(schieber)gatter	$\begin{pmatrix} 1 & 0 \\ 0 & e^{\frac{i \pi}{4}} \end{pmatrix}$	Dreht die Phase 90° (π/2) um die Z-Achse
	Allgemeines Phasen(schieber)gatter2,3	$\begin{pmatrix} 1 & 0 \\ 0 & e^{\frac{i \pi}{2^k}} \end{pmatrix}$	k wird willkürlich festgelegt Dreht die Phase bei k=0 oder k=1 180° (π) um die Z-Achse. Bei k=2 sind es 90° (π/4).
	S-Gatter4	$\begin{pmatrix} 1 & 0 \\ 0 & i \end{pmatrix}$	Dreht die Phase 90° (π/2) um die Z-Achse
	Willkürliches unitäres Gatter3	$\begin{pmatrix} a & b \\ -b^* & a^* \end{pmatrix}$ mit $\left|a\right|^2+\left|b\right|^2=1$	Alle Eigenschaften werden willkürlich festgelegt
1Am Beispiel drei verschiedener Eingangssignale mit verschiedenen Spins und deren Lage nach dem Durchqueren des Gatters. Die Z-Achse (am Eingang Blau) gibt den reellen Wert, die X- (am Eingang Rot) und Y-Achse (am Eingang Grün) die Phasenlage wieder. Der Eingang ist mit A, der Ausgang mit A' gekennzeichnet. 2Ausgang dargestellt für die Werte k=0, k=1 und k=2 3Ausgang abhängig von den verwendeten Parametern 4Erzielt im gezeigten Fall dasselbe Ergebnis

Quantengatter mit zwei Eingängen

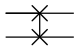
Quantengatter, die sich auf zwei Quantenbits beziehen

Symbol	Bezeichnung	Funktion	Beschreibung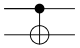
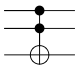
	Kontrolliertes-Nicht-Gatter (CNOT, XOR-Verknüpfung)	$\left| 00 \right\rangle \to \left| 00 \right\rangle$ $\left| 01 \right\rangle \to \left| 01 \right\rangle$ $\left| 10 \right\rangle \to \left| 11 \right\rangle$ $\left| 11 \right\rangle \to \left| 10 \right\rangle$	Der reelle Wert des zweiten Qubits (B) wird in Abhängigkeit vom reellen Wert des ersten Qubits (A) entweder beibehalten (A=0) oder negiert (A=1). $B' \leftarrow A \oplus B = \left( \neg A \land B \right) \vee \left( \neg B \land A \right)$ Der Wert des ersten Qubits wird beibehalten. $A' \leftarrow A \,$
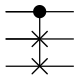
	Austauschknoten ("Swap")	$\left| 00 \right\rangle \to \left| 00 \right\rangle$ $\left| 01 \right\rangle \to \left| 10 \right\rangle$ $\left| 10 \right\rangle \to \left| 01 \right\rangle$ $\left| 11 \right\rangle \to \left| 11 \right\rangle$	Die beiden Eingangs-Qubits werden vertauscht
	Kontrollierte Phase (C-Phase)	${ \left| 11 \right\rangle } \to e^{\frac{2 i \pi}{2^k} } \cdot { \left| 11 \right\rangle }$	k kann beliebig gewählt werden.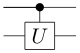
	Kontrolliertes U	$\left| 0\phi \right\rangle \to \left| 0 \phi \right\rangle$ $\left| 1\phi \right\rangle \to \left| 1 \right\rangle\begin{pmatrix} a & b \\ c & d \end{pmatrix} \cdot \left| \phi \right\rangle$	Das zweite Qubit wird gemäss der unitären Abbildung U transformiert falls das erste Qubit den Wert "1" hat und bleibt ansonsten unverändert. (C-NOT und C-Phase sind Spezialfälle von C-U)
	Beliebige unitäre Transformation	$\left| \psi \right\rangle \to U \cdot \left| \psi \right\rangle$	Die unabhängigen Variablen der komplexen unitären 4x4-Matrix (16 reelle Parameter) können beliebig gewählt werden. Auf diese Weise kann man alle Wechselwirkungen zwischen den beiden Qubits beschreiben.

Quantengatter mit drei Eingängen

Quantengatter, die sich auf drei Quantenbits beziehen.

Symbol	Bezeichnung	Funktion	Beschreibung
	Toffoli-Gatter	$\left| 111 \right\rangle \leftrightarrow \left| 110 \right\rangle$ $\left| 0yx \right\rangle \leftrightarrow \left| 0yx \right\rangle$ $\left| 10x \right\rangle \leftrightarrow \left| 10x \right\rangle$ $\begin{pmatrix} 1 & 0 \\ 1 & 1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x \\ x \oplus y \end{pmatrix}$	Die ersten beiden Qubits (A und B) bleiben unverändert. $A' \leftarrow A\,$ $B' \leftarrow B\,$ Der reelle Weert des dritten Qubits (C) wird negiert, wenn der reelle Wert der ersten beiden Qubits positiv (d.h. logisch 1) ist. $C' \leftarrow C \oplus \left( A \land B \right)\,$
	Fredkin-Gatter	$\left| 001 \right\rangle \leftrightarrow \left| 010 \right\rangle$ $\left| 010 \right\rangle \leftrightarrow \left| 001 \right\rangle$ $\left| 101 \right\rangle \leftrightarrow \left| 101 \right\rangle$ $\left| 101 \right\rangle \leftrightarrow \left| 101 \right\rangle$ …	Das Fredkin-Gatter vertauscht das zweite und dritte Qubit, wenn der reelle Wert des ersten Qubits negativ (d.h. logisch 0) ist.
	Deutsch-Gatter	$|11x \rangle \rightarrow |11(1-x)\rangle \cdot \sin(\theta) + i \cdot |11x \rangle \cdot \cos(\theta)$	Das Deutsch-Gatter ist ein universelles Drei-Qubit-Gatter, mit dem beliebige Wechselwirkungen der ersten beiden Qubits auf das dritte Qubit erfolgen können. Die ersten beiden Qubits werden nicht verändert.1

Siehe auch

• Quantengatter
• Quaternion
• Qubit