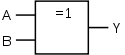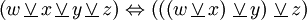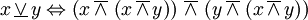XOR-Verknüpfung

Gatter-Typen
	NOT
AND	NAND
OR	NOR
XOR	XNOR

Ein XOR-Gatter (von engl. eXclusive OR - exklusives Oder, entweder oder) ist ein Gatter mit mehreren Eingängen und einem Ausgang, bei dem der Ausgang genau dann logisch „1“ ist, wenn an einer ungeraden Anzahl von Eingängen „1“ anliegt und an den restlichen „0“. Die XOR-Verknüpfung wird auch als Anti- oder Kontravalenz bezeichnet.

Für den einfachen Fall eines XOR-Gatters mit zwei Eingängen bedeutet das, dass die Eingänge verschieden beschaltet sein müssen, um am Ausgang eine „1“ zu erhalten. Entweder an dem einen oder am anderen Eingang muss „1“ anliegen. Im Unterschied zu einer einfachen OR-Verknüpfung gilt die Bedingung als nicht erfüllt, wenn an beiden Eingängen eine „1“ anliegt. Bei XOR ist das Ergebnis in diesem Fall eine „0“.

Symbolik

In der Literatur wird das Exklusiv-Oder mit verschiedenen Symbolen gekennzeichnet. Üblich ist es, den Operator als „XOR“ auszuschreiben, z. B. mit dem Ausdruck "A XOR B". Bei Verwendung des Symbols „+“ für das logische Oder wird das Symbol „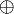$\oplus$“ für das Exklusiv-Oder verwendet. Bei der Verwendung von „∨“ für das logische Oder wird hingegen „⊻“ für das Exklusiv-Oder verwendet. Als Bitweiser Operator findet das Zeichen ^ Verwendung.

Siehe dazu auch die Notation und Aussprache des Kontravalentors.

Übersicht

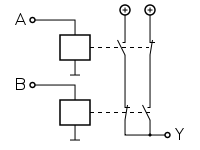
Funktion	Schaltsymbol			Wahrheitstabelle	Relais-Logik
	IEC 60617-12	US ANSI 91-1984	DIN 40700 (vor 1976)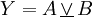
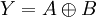
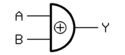
$Y = A \,\underline{\lor}\, B$ $Y = A \oplus B$			oder	A B Y = A ⊻ B 0 0 0 0 1 1 1 0 1 1 1 0

Synthese

Die Funktion eines XOR-Gatters mit mehr als zwei Eingängen ergibt sich, indem man zunächst zwei der Eingänge XOR-verknüpft, dann deren Ergebnis mit dem nächsten Eingang XOR-verknüpft, solange bis alle Eingänge berücksichtigt sind.

$\left( w \,\underline{\lor}\, x \,\underline{\lor}\, y \,\underline{\lor}\, z \right) \Leftrightarrow \left( \left( \left( w \,\underline{\lor}\, x \right) \,\underline{\lor}\, y \right) \,\underline{\lor}\, z \right)$

Die Reihenfolge der Eingänge ist dabei egal. Die XOR-Verknüpfung erfüllt das Assoziativgesetz.

XOR
Aufbau eines XOR-Gatters aus vier NAND-Gattern	Aufbau eines XOR-Gatters aus Und- und Oder-Gattern

Die linke Abbildung zeigt den Aufbau eines XOR-Gatters aus vier NAND-Bausteinen gemäß der logischen Antivalenz

$x \,\underline{\lor}\, y \Leftrightarrow \left( x \,\overline{\land}\, \left( x \,\overline{\land}\, y \right) \right) \,\overline{\land}\, \left( y \,\overline{\land}\, \left( x \,\overline{\land}\, y \right) \right)$

Programmierung

Die XOR-Verknüpfung lässt sich auch durch die Addition zweier Bits modulo 2 berechnen: ist die Summe eine gerade Zahl, ergibt sich 0; ist sie ungerade, ergibt sich 1. Weiterhin kann man die Verknüpfung auch als Anzeige der Ungleichheit der Eingangsbits ansehen.

Anwendung

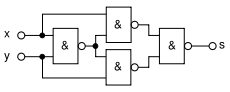
Anwendung des XOR zur Addition von binären Zahlen

Ein XOR-Gatter kann zur Addition von binären Zahlen eingesetzt werden. Hier wird zusätzlich, zum Beispiel mit Hilfe eines AND-Gatters, beim Zustand x=1 und y=1 ein sogenannter Übertrag =1 gebildet. Dieser Übertrag ist bei der Addition des nächsthöheren Bits als „1“ zu berücksichtigen. Der Addierer des Von-Neumann-Addierwerks benutzt diese Logik.

Anwendungsbeispiel in der Kryptografie

Das nachweislich sichere Verschlüsselungsverfahren One-Time-Pad wird meist unter Zuhilfenahme einer XOR-Verknüpfung implementiert. Die zu verschlüsselnde Nachricht (Klartext) wird dazu zuerst als Bitfolge kodiert. Eine zweite zufällige Bitfolge, die genauso lang wie die Nachricht ist, wird als Schlüssel verwendet. Der Geheimtext entsteht, indem das erste Bit der Nachricht mit dem ersten Bit des Schlüssels XOR-verknüpft wird, anschließend das zweite Bit mit dem Zweiten usw. Führt man anschließend die gleiche XOR-Verknüpfung mit dem Geheimtext und dem Schlüssel aus, so erhält man wieder die ursprüngliche Nachricht.

Anwendungsbeispiel im RAID-System

101 XOR 011 = 110
110 XOR 011 = 101
110 XOR 101 = 011

Aus zwei dreistelligen Bitfolgen, angenommen 101 und 011, wird mittels der XOR-Verknüpfung die Parität gebildet: 110 (erste Zeile im Beispiel rechts). Geht nun die erste Bitfolge (101) verloren, so kann sie wiederhergestellt werden, indem die zweite Bitfolge (011) mit der Parität XOR-verknüpft wird (zweite Zeile).

Frequenzverdopplung

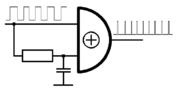
Frequenzverdopplung eines digitalen Signals

Eine sehr einfache Frequenzverdopplung von Rechteckschwingungen im Frequenzbereich bis zu einigen 100 MHz kann man mit einem XOR-Gatter erzielen, wenn man einen Eingang unmittelbar und den anderen mit einen geringfügig verzögerten Signal (RC-Glied) speist. Die entstehenden Nadelimpulse sind phasengebunden und etwa so kurz wie die Zeitkonstante des RC-Gliedes. Da dieses Verfahren keine Resonanzfilter verwendet, kann das Eingangssignal beliebige Tastverhältnisse besitzen bzw. stark frequenzmoduliert sein.

Realisierung

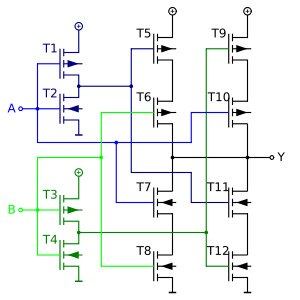
CMOS

Schaltbild in CMOS-Technologie

Die zuvor gezeigte Realisierung aus Und- und Oder-Gattern benötigt in CMOS-Technologie 16 Transistoren. Eine direkte Umsetzung (rechts) benötigt nur 12 Transistoren und mit Tricks, unter Einbußen bei der Geschwindigkeit, sogar nur 6 Transistoren. Zum Verständnis: T1+T2 und T3+T4 invertieren die Eingangssignale. Bei High-Potential an beiden Eingängen (A+B) leiten T7+T8 und ziehen den Ausgang Y auf Low-Potential. Sind beide Eingänge auf Low-Potential leiten T11+T12, da vor beiden ein Inverter liegt und das Eingangssignal umkehrt.

Siehe auch

• Aussagenlogik