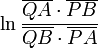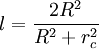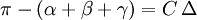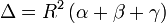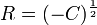Lobatschewskische Geometrie

Modell einer Parkettierung einer Ebene mit Quadraten. An den Ecken treffen dabei mehr als vier zusammen (je nach Größe, hier fünf).

Die hyperbolische Geometrie als Beispiel für eine nichteuklidische Geometrie erhält man, wenn man anstelle des Parallelenaxioms eine seiner Verneinungen, das „hyperbolische Axiom“ annimmt. Dieses besagt, dass es zu einer Geraden g und einem Punkt P nicht wie in der euklidischen Geometrie nur genau eine, sondern mindestens zwei Geraden (h und i) gibt, die durch P gehen und zu g parallel sind. Dass zwei Geraden „parallel“ zueinander sind, bedeutet hier aber lediglich, dass sie keine gemeinsamen Punkte haben, nicht dass sie überall den gleichen Abstand haben (h und i haben nur einen gemeinsamen Punkt P).

Es lässt sich zeigen, dass es dann durch den Punkt unendlich viele Nichtschneidende („Parallelen“) zu der Geraden gibt. Zwei davon sind in einer Grenzlage und heißen grenzparallel (auch: horoparallel) zur Geraden, während die restlichen Geraden überparallel (auch: hyperparallel) genannt werden.

Ein einfaches Modell zum Veranschaulichen einer solchen Geometrie ist das Kleinsche-Modell: Die „Ebene“ ist hier eine offene Kreisscheibe („offen“ bedeutet, dass der Rand des Kreises nicht zur Ebene dazugehört), und die „Geraden“ sind Kreisbögen, die senkrecht auf dem Rand stehen. Ein Nachteil dieses Modells ist, dass es die Längen- und Winkelmessung verkompliziert, da man eine spezielle Distanzfunktion verwenden muss.

Distanzfunktion

Abstand zweier Punkte in einer hyperbolischen Geometrie

Zwei Punkte A und B in der hyperbolischen Geometrie haben den Abstand

$\ln \frac{\overline{QA}\cdot\overline{PB}}{\overline{QB}\cdot\overline{PA}}$

oder

$\frac{1}{2} \ln \frac{\overline{RA}\cdot\overline{SB}}{\overline{RB} \cdot \overline{SA}}$.

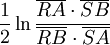Um die Punkte A und B von der konformen Linie (in der Abbildung grün) auf die projektive Linie (in der Abbildung rot) zu projizieren, werden die Punkte mit Bezug auf den Mittelpunkt M mit dem Faktor

$l = \frac{2 R^2}{R^2 + r_c^2}$

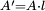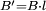skaliert (dh. ${}_{A' = A\cdot l}$ und ${}_{B' = B\cdot l}$). Hierbei ist R der Radius des Kreises welcher die hyperbolische Geometrie umgibt. Weiters ist r_c die Euklidsche Distanz zwischen dem Mittelpunkt M und dem zu transformierenden Punkt A bzw. B.

Dreieck

Dreieck im hyperbolischen Raum

In der hyperbolischen Geometrie ist die Winkelsumme in einem Dreieck immer kleiner als π (180 Grad; bzw. zwei Rechte, wenn man das Winkelmaß vermeiden will). Für sehr große Dreiecke kann sie beliebig klein werden. Die Fläche des Dreiecks wird nach Johann Heinrich Lamberts Formel berechnet:

$\pi - ( \alpha + \beta + \gamma ) = C\,\Delta$

Wobei α, β und γ die jeweiligen Winkel, Δ die Fläche und die Konstante C ein Skalierungsfaktor ist. Der Skalierungsfaktor C ist abhängig vom verwendeten Einheitensystem und im Grunde gleich 1 zu setzen. Ist der Faktor C negativ spricht man von einer Gaußschen Krümmung. Analog dazu definierte Thomas Hariot zuvor im Jahr 1603 die Formel

$\Delta = R^2 \,(\alpha + \beta + \gamma)$

für die Fläche eines Dreiecks auf einer Kugeloberfläche, welches von Kreisen mit demselben Radius wie die Kugel gebildet wird. Hiebei gilt der Zusammenhang

$C = -\frac{1}{R^2}$.

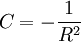Da für die hyperbolische Geometrie ein positiver Wert für K erforderlich ist, muss es sich bei R aufgrund von

$R = (-C)^\frac{1}{2}$

um einen imaginären Radius handeln.

Quadrat

In der hyperbolischen Geometrie ist der Winkel der Ecke in einem Quadrat (hyperbolisches Quadrat) immer kleiner als ${}_{\frac{\pi}{2}}$ (90°). Ein Quadrat, dessen Eckpunkte auf dem Umkreis der hyperbolischen Geometrie liegen, weist einen Winkel von ${}_{\frac{2}{5}\,\pi}$ (72°) auf.

Siehe auch

• Elliptische Geometrie
• Nikolai Lobatschewski
• János Bolyai
• Felix Klein
• Giovanni Gerolamo Saccheri

Literatur

• Marvin Jay Greenberg, Euclidean & Non-Euclidean Geometries: Development and History, W. H. Freeman, 1993, ISBN 978-0-7167-2446-9