- Lovász Local Lemma
-
Das Lovász-Local-Lemma ist ein Hilfssatz aus der Wahrscheinlichkeitstheorie. Es verallgemeinert das Argument, dass die stochastische Unabhängigkeit von Ereignissen mit positiver Ausfallwahrscheinlichkeit eine positive Wahrscheinlichkeit für den Ausfall aller Ereignisse impliziert, auf Situationen, in denen nicht alle Ereignisse unabhängig sind. Sein Name beruht darauf, dass es lokale Eigenschaften zu einem globalen Ergebnis zusammensetzt. Es findet am häufigsten Anwendung in probabilistischen Ansätzen, um Existenzbeweise zu führen. 1975 wurde es von László Lovász und Paul Erdős bewiesen.
Inhaltsverzeichnis
Aussage des Lemmas
Allgemeine Version
Sei
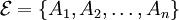 eine Menge von Ereignissen über einem beliebigen Wahrscheinlichkeitsraum, so dass jedes Ereignis Ai stochastisch unabhängig von allen anderen bis auf
eine Menge von Ereignissen über einem beliebigen Wahrscheinlichkeitsraum, so dass jedes Ereignis Ai stochastisch unabhängig von allen anderen bis auf 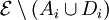 für jeweils ein
für jeweils ein 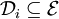 ist.
ist.Falls reelle Zahlen
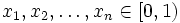 existieren, so dass für alle
existieren, so dass für alle 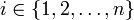 gilt:
gilt: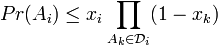 ,
,
so folgt:
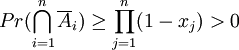 .
.
In vielen Beweisen wird der folgende symmetrische Spezialfall verwendet.Symmetrische Version
Sei
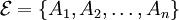 eine Menge von Ereignissen über einem beliebigen Wahrscheinlichkeitsraum, so dass jedes Ereignis aus
eine Menge von Ereignissen über einem beliebigen Wahrscheinlichkeitsraum, so dass jedes Ereignis aus 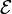 von höchstens d anderen Ereignissen stochastisch abhängig ist.
von höchstens d anderen Ereignissen stochastisch abhängig ist.Falls
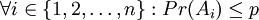 , wobei
, wobei ![p \in [0,1]](/pictures/dewiki/53/550abf67410399d394e58560a62f657a.png) ,
,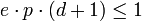 ,
,
so folgt
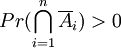 .
.Anwendungsbeispiel
Sei
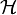 ein Hypergraph, so dass jede Hyperkante mindestens k Knoten enthält und sich mit höchstens 2k − 3 weiteren Hyperkanten schneidet. Dann ist
ein Hypergraph, so dass jede Hyperkante mindestens k Knoten enthält und sich mit höchstens 2k − 3 weiteren Hyperkanten schneidet. Dann ist 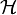 2-färbbar.
2-färbbar.Färbe die Knoten von
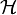 zunächst zufällig, unabhängig und gleichverteilt mit zwei Farben (d.h. die Wahrscheinlichkeit, dass ein Knoten beispielsweise rot oder blau ist, beträgt jeweils
zunächst zufällig, unabhängig und gleichverteilt mit zwei Farben (d.h. die Wahrscheinlichkeit, dass ein Knoten beispielsweise rot oder blau ist, beträgt jeweils  ). Setze
). Setze 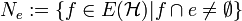 für alle Hyperkanten
für alle Hyperkanten 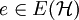 : Wende nun das symmetrische Local-Lemma auf die Menge
: Wende nun das symmetrische Local-Lemma auf die Menge 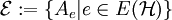 an: Zunächst ist jedes Ereignis Ae stochastisch abhängig von Ne, da sich jede Kante aus Ne per Definition mindestens einen Knoten mit e teilt. Nach Voraussetzung gilt:
an: Zunächst ist jedes Ereignis Ae stochastisch abhängig von Ne, da sich jede Kante aus Ne per Definition mindestens einen Knoten mit e teilt. Nach Voraussetzung gilt: 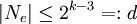 für alle Kanten
für alle Kanten 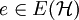 . Andererseits ist jedes Ereignis Ae stochastisch unabhängig von
. Andererseits ist jedes Ereignis Ae stochastisch unabhängig von 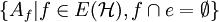 , da die Knoten unabhängig voneinander gefärbt wurden. Da
, da die Knoten unabhängig voneinander gefärbt wurden. Da 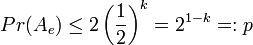 ist, gilt:
ist, gilt: 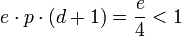 . Also ist
. Also ist 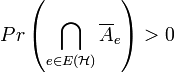 , das heißt:
, das heißt: 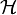 ist 2-färbbar.
ist 2-färbbar.Literatur
- Michael Molloy; Bruce Reed: Graph Colouring and the Probabilistic Method. Springer, 2002, ISBN 3540421394, S. 221-229.
Wikimedia Foundation.
