M-Theorie

M-Theorie
Die fünf Stringtheorien und 11-dimensionale Supergravitation als Grenzfälle der M-Theorie.

Die M-Theorie ist der Versuch einer Erweiterung und Verallgemeinerung der Stringtheorie in der Theoretischen Physik. Diese Theorie ist das Gebiet intensiver Forschung, da man hofft, mit ihr alle bekannten Naturkräfte einheitlich beschreiben zu können.

Inhaltsverzeichnis

Details

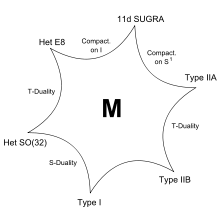
Die M-Theorie wurde während der so genannten zweiten Superstringrevolution geboren, wobei wesentliche Beiträge von Edward Witten stammen, der darüber 1995 auf einer Konferenz an der University of Southern California einen vielbeachteten Vortrag hielt. Hierbei werden die fünf bekannten Superstringtheorien, Type I, Type IIA und IIB, sowie die beiden Heterotischen Stringtheorien (im Bild mit E8 und SO(32) bezeichnet) und die elfdimensionale Supergravitation als Grenzfälle einer fundamentaleren Theorie betrachtet.

Die Verbindungen zwischen den verschiedenen Theorien sind durch Dualitäten gegeben, wie S-Dualität und T-Dualität. Mit ihrer Hilfe kann man zeigen, dass die unterschiedlichen Theorien die gleichen Ergebnisse berechnen, allerdings in unterschiedlichen Bereichen ihres Parameterraumes. Damit ist es möglich, Aussagen über die zugrundeliegende Theorie in verschiedenen Grenzbereichen zu machen, obwohl eine explizite Formulierung nicht bekannt ist.

Die elfdimensionale Supergravitation nimmt in gewisser Weise eine Sonderstellung ein, da sie in 11 Dimensionen formuliert ist (und damit die maximale Anzahl von Dimensionen für eine Supergravitationstheorie besitzt), im Gegensatz zu den Stringtheorien, welche in 10 Dimensionen formuliert sind. Elfdimensionale Supergravitation ist außerdem eine klassische (d.h. nicht quantisierte) Theorie, wohingegen die Stringtheorien Quantentheorien sind. Die Verbindung zwischen der Heterotischen E8xE8 Stringtheorie bzw. Type IIA zur Supergravitation wird durch eine Kompaktifizierung der 11. Dimension auf einem Intervall (in der Abbildung mit I bezeichnet) bzw. auf einem Kreis (S1) erreicht. Außerdem betrachtet man auf der Stringseite den Supergravitations-Limes der Theorie.

Nichtperturbative Aussagen zur M-Theorie lassen sich mit Hilfe von D-Branen bzw. M-Branen machen. Allerdings gibt es zur Zeit noch keine vollständige nichtperturbative Formulierung der M-Theorie, was auch damit zusammenhängt, dass sich für mehr als eindimensionale Objekte keine konforme Feldtheorie konstruieren lässt (siehe Polyakov-Wirkung).

Die angegebene Bedeutung für den Buchstaben M in der Bezeichnung der Theorie ist nicht einheitlich. Nach Edward Witten, der den Begriff einführte[1], steht er für „Magie, Rätsel (englisch Mystery) oder Membran - je nach Geschmack“[2]. Weitere Kandidaten, die genannt wurden, waren Matrix (nach einem Vorschlag für die M-Theorie von Tom Banks und anderen), Mutter aller Stringtheorien[3] und es wurde sogar vermutet es stehe für ein umgedrehtes „W“ als Synonym für „Witten“ oder dass der Buchstabe „M“ als einziger Buchstabe neben dem „W“ fünf Punkte harmonisch verbindet, wobei die fünf Punkte für die fünf zuvor widersprüchlichen Stringtheorien stehen.

Literatur

Weblinks

Einzelnachweise

  1. ↑ Michio Kaku Into the eleventh dimension, Online
  2. ↑ M stands for magic, mystery or membrane -according to taste, zitiert nach Duff The theory formerly known as strings, Scientific American 1998, S. 12
  3. ↑ Kaku, loc. cit.

Wikimedia Foundation.

Игры ⚽ Нужна курсовая?

Schlagen Sie auch in anderen Wörterbüchern nach:

  • théorie — [ teɔri ] n. f. • 1496; « science de la contemplation » 1380; rare av. XVIIe; lat. ecclés. theoria, mot gr. « observation, contemplation », de theôrein « observer » I ♦ 1 ♦ Ensemble d idées, de concepts abstraits, plus ou moins organisés,… …   Encyclopédie Universelle

  • Theorie axiomatique des ensembles — Théorie des ensembles La théorie des ensembles est une branche des mathématiques, créée par le mathématicien allemand Georg Cantor à la fin du XIXe siècle. La théorie des ensembles se donne comme primitives les notions d ensemble et d… …   Wikipédia en Français

  • Theorie de Galois — Théorie de Galois Évariste Galois 1811 1832 En mathématiques et plus précisément en algèbre, la théorie de Galois est l étude des extensions de corps commutatifs, par le biais d une correspondance avec des groupes de transformations sur ces… …   Wikipédia en Français

  • Theorie des cordes — Théorie des cordes Les niveaux de grossissements : monde macroscopique, monde moléculaire, monde atomique, monde subatomique, monde des cordes. La théorie des cordes est l une des voies envisagées pour régler une des questions majeures de la …   Wikipédia en Français

  • Theorie des ensembles — Théorie des ensembles La théorie des ensembles est une branche des mathématiques, créée par le mathématicien allemand Georg Cantor à la fin du XIXe siècle. La théorie des ensembles se donne comme primitives les notions d ensemble et d… …   Wikipédia en Français

  • Théorie axiomatique des ensembles — Théorie des ensembles La théorie des ensembles est une branche des mathématiques, créée par le mathématicien allemand Georg Cantor à la fin du XIXe siècle. La théorie des ensembles se donne comme primitives les notions d ensemble et d… …   Wikipédia en Français

  • Théorie de galois — Évariste Galois 1811 1832 En mathématiques et plus précisément en algèbre, la théorie de Galois est l étude des extensions de corps commutatifs, par le biais d une correspondance avec des groupes de transformations sur ces extensions, les groupes …   Wikipédia en Français

  • Theorie axiomatique — Théorie axiomatique Quand on parle de théorie mathématique on fait référence à une somme d énoncés, de définitions, de méthodes de preuve etc. Par exemple, quand dans cet article on parle de théorie de la calculabilité c est en ce sens. Par… …   Wikipédia en Français

  • Theorie des ensembles de von Neumann-Bernays-Godel — Théorie des ensembles de von Neumann–Bernays–Gödel La théorie des ensembles de von Neumann–Bernays–Gödel, abrégée en NBG ou théorie des classes, est une théorie axiomatique essentiellement équivalente[1] à la théorie ZFC de Zermelo–Fraenkel avec… …   Wikipédia en Français

  • Theorie des ensembles de von Neumann–Bernays–Godel — Théorie des ensembles de von Neumann–Bernays–Gödel La théorie des ensembles de von Neumann–Bernays–Gödel, abrégée en NBG ou théorie des classes, est une théorie axiomatique essentiellement équivalente[1] à la théorie ZFC de Zermelo–Fraenkel avec… …   Wikipédia en Français

  • Theorie des nombres — Théorie des nombres Traditionnellement, la théorie des nombres est une branche des mathématiques qui s occupe des propriétés des nombres entiers, qu ils soient entiers naturels ou entiers relatifs, et contient beaucoup de problèmes ouverts qu il… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”