Mandelstam-Variable

Die Mandelstam-Variablen werden in der theoretischen Physik und in der Teilchenphysik zur Beschreibung von Zwei-Teilchen-Streuprozessen verwendet. Hierbei leitet man aus den Impulsen der vier an dem Streuprozess beteiligten Teilchen Lorentz-invariante Größen ab, die Mandelstam-Variablen s, t und u, die wie folgt definiert sind:

s = (p₁ + p₂)² = (p₃ + p₄)²

t = (p₁ − p₃)² = (p₂ − p₄)²

u = (p₁ − p₄)² = (p₂ − p₃)²

Hierin sind p₁ und p₂ die Viererimpulse der einlaufenden und p₃ und p₄ die Impulse der auslaufenden (gestreuten) Teilchen.

Eine besondere Bedeutung haben s und t: s ist das Quadrat der Schwerpunktsenergie und t das Quadrat des Viererimpulsübertrags. Die Summe der Mandelstam-Variablen ist gleich der Summe der Massenquadrate der beteiligten Teilchen:

$s+t+u = \sum_{i=1}^4 m_i^2$

Benannt sind die Mandelstam-Variablen nach Stanley Mandelstam, der sie 1958 einführte.

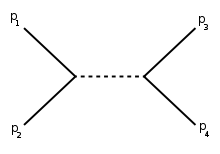
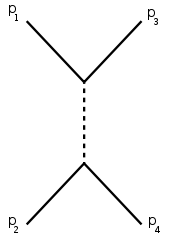
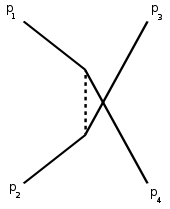
s-, t- und u-Kanal

In Anlehnung an die Definition der Mandelstam-Variablen unterteilt man Zwei-Teilchen-Streuprozesse in s-, t- und u-Kanal-Prozesse. Die zugehörigen Feynman-Diagramme sind in den folgenden Abbildung gezeigt.

s-Kanal

t-Kanal

u-Kanal

Die Darstellung folgt der Konvention, nach der die Zeitachse nach rechts verläuft. Die Zwischenzustände (Linien ohne freies Ende) bezeichnet man als virtuelle Teilchen. Der quadrierte Viererimpuls dieses Teilchens ist entsprechend gleich s, t oder u.