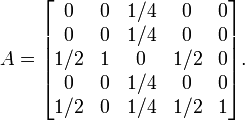Markov-Matrix

In der Mathematik, besonders der Wahrscheinlichkeitstheorie und Statistik bezeichnet eine Übergangsmatrix eine quadratische Matrix, deren Zeilen- oder Spaltensummen Eins betragen und deren Elemente zwischen Null und Eins liegen. Eine Übergangsmatrix kann als Repräsentation der Übergangswahrscheinlichkeiten einer diskreten, endlichen Markow-Kette gesehen werden.

Beispiel für eine Übergangsmatrix P

$P = \begin{bmatrix} 0.5 & 0.3 & 0.2 \\ 0.2 & 0.4 & 0.4 \\ 0.3 & 0.3 & 0.4 \end{bmatrix}$

Anwendung zur Charakterisierung diskreter Markow-Ketten

Wenn Zustandswahrscheinlichkeiten in Zeilenvektoren geschrieben werden, bezeichnet das Matrizenelement p_ij, wobei i die Zeilennummer und j die Spaltennummer darstellt, die Wahrscheinlichkeit eines Übergangs vom Zustand i in den Zustand j. Hier müssen jeweils die Zeilensummen gleich 1 sein.

Dadurch lässt sich durch die Multiplikation eines Zustandswahrscheinlichkeitsvektors mit der Übergangsmatrix der Zustandswahrscheinlichkeitsvektor für den nächsten Zustand bestimmen. Folglich lässt sich die Zustandswahrscheinlichkeit für den übernächsten Zustand durch Multiplikation mit dem Quadrat der Übergangsmatrix bestimmen etc. pp.

Eine besondere Rolle kommt den Eigenvektoren dieser Matrix zu, denn diese stellen die Grenzverteilung der Markow-Kette nach langer Zeit dar, wenn diese eine vom Anfangszustand unabhängige ergodische Verteilung besitzt.

Eine Beispielrechnung: Die Katze und die Maus

Wir stellen uns vor, wir hätten fünf nebeneinander liegende Boxen, durchnummeriert von eins bis fünf, und in der ersten Box möge sich die Katze und in der letzten die Maus befinden. Nach einer festen Rundenzeit wechseln die Tiere zufällig in eine Nachbarbox. Das makabre Spiel hat ein Ende, wenn die Katze in einer Box auf die Maus trifft. Wir bezeichnen die möglichen Zustände mit (i,j), d. h. die Katze ist in der i-ten und die Maus in der j-ten Box. Wir sehen sofort, dass wenn i gerade (ungerade) ist, j ebenfalls gerade (ungerade) sein muss. Sofort ist auch klar, dass 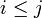$i\le j$ gelten muss. Die Markow-Kette, die dieses Spiel beschreibt, hat also die folgenden fünf Zustände:

   * (1,3)
   * (1,5)
   * (2,4)
   * (3,5)
   * Spielende (2,2), (3,3) und (4,4).

Die Übergangsmatrix A dazu ist nun

$A = \begin{bmatrix} 0 & 0 & 1/4 & 0 & 0 \\ 0 & 0 & 1/4 & 0 & 0 \\ 1/2 & 1 & 0 & 1/2 & 0 \\ 0 & 0 & 1/4 & 0 & 0 \\ 1/2 & 0 & 1/4 & 1/2 & 1 \end{bmatrix}.$

Wenn wir beispielsweise wie zu Beginn im Zustand v = [0,1,0,0,0] sind, dann wechseln wir mit Sicherheit in den Zustand v = [0,0,1,0,0], also Katze in der zweiten und Maus in der vierten Box. Von diesem Zustand ausgehend kommen wir nun aber mit 25% Wahrscheinlichkeit in einen der anderen vier Zustände.

Wir sind nun an der durchschnittlichen Spieldauer interessiert, Sei R die Rundenanzahl, dann gilt 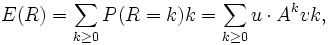$E(R)=\sum_{k\ge 0} P(R= k) k=\sum_{k\ge 0} u \cdot A^k v k,$ wobei u = [1 / 2,0,1 / 4,1 / 2,0] ist (vergleiche mit der letzten Zeile von A).

Wir wenden nun den Trick an, dass 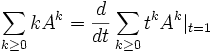$\sum_{k\ge 0} k A^k = \frac{d}{dt} \sum_{k\ge 0} t^k A^k|_{t=1}$ ist. Formal erhalten wir mit der Neumann-Reihe 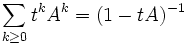$\sum_{k\ge 0} t^k A^k =(1-tA)^{-1}$, wobei wir mit 1 die Einheitsmatrix bezeichneten. Wir differenzieren nun und erhalten (1 − tA) ^{− 2}A. Wenn wir nun 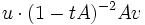$u \cdot (1-tA)^{-2} A v$ berechnen und t=1 setzen, bekommen wir das Ergebnis, im Mittel dauert das Spiel 9 / 2 Runden.

Siehe auch

Übergangstabelle