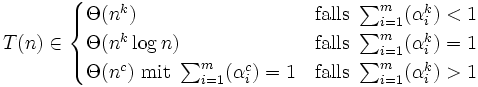- Mastertheorem
-
Der Begriff Hauptsatz der Laufzeitfunktionen oder oft englisch Master-Theorem, das ein Spezialfall des Akra-Bazzi-Theorems ist, bietet eine schnelle Lösung für die Frage, in welcher Laufzeitklasse eine gegebene rekursiv definierte Funktion liegt. Jedoch kann mit dem Master-Theorem nicht jede rekursiv definierte Funktion gelöst werden. Lässt sich keiner der drei möglichen Fälle des Master-Theorems auf die Funktion T anwenden, so muss man die Komplexitätsklasse der Funktion anderweitig berechnen.
Inhaltsverzeichnis
Allgemeine Form
Die allgemeine Form für die Anwendung des Master-Theorems sieht wie folgt aus:
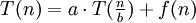
Hierbei steht T(n) für die zu untersuchende Laufzeitfunktion, während a und b Konstanten sind. Ferner bezeichnet f(n) eine von T(n) unabhängige und nicht negative Funktion. Damit das Master-Theorem angewendet werden kann, muss für die beiden Konstanten die Bedingung a ≥ 1 und b > 1 erfüllt sein.
Interpretation der Rekurrenz T(n):
- a = Anzahl der Unterprobleme in der Rekursion
- 1 / b = Teil des Originalproblems, welches wiederum durch alle Unterprobleme repräsentiert wird
- f(n) = Kosten (Aufwand) die durch die Division des Problems und der Kombination der Teillösungen entstehen
Weiterhin benötigt man für die Benutzung des Master-Theorems noch den Logarithmus von a zur Basis b (logba), welchen man aus den beiden Größen a und b errechnen kann.
Das Master-Theorem unterscheidet sich in drei Fälle, wobei sich höchstens ein Fall auf die gegebene Rekursion anwenden lässt. Passt keiner der Fälle, so lässt sich das Master-Theorem nicht anwenden und man muss sich anderer Methoden bedienen.
Erster Fall Zweiter Fall Dritter Fall Allgemein Falls gilt: 
für ein
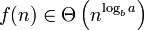
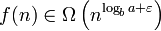 für ein
für ein 
und ebenfalls für ein c mit 0 < c < 1 und hinreichend große n gilt: 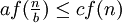
Dann folgt: 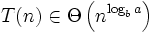
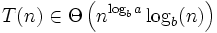
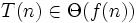
Beispiel 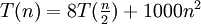
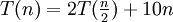
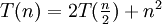
Aus der Formel ist folgendes abzulesen: a = 8, b = 2 f(n) = 1000n2 logba = log28 = 3 a = 2, b = 2 f(n) = 10n logba = log22 = 1 a = 2, b = 2 f(n) = n2 logba = log22 = 1 1. Bedingung: 
für ein
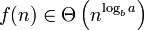
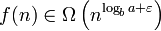 für ein
für ein 
Werte einsetzen: 
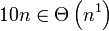
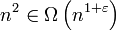
Wähle  :
: mit
mit 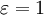 √
√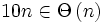 √
√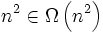 mit
mit 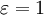 √
√2. Bedingung: (nur im 3. Fall) 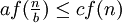
Setze auch hier obige Werte ein: 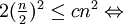
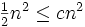
Wähle c = ½: 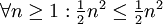 √
√Damit gilt für die Laufzeitfunktion: 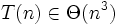
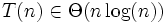
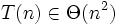
( √ = Wahre Aussage )
Verallgemeinerung des zweiten Falls
Nicht alle Rekurrenzgleichungen lassen sich mithilfe einer der drei Fällen des Mastertheorems lösen. So ist zum Beispiel die folgende Rekurrenzgleichung nicht direkt mit dem Mastertheorem lösbar.
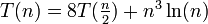 .
.Auf den ersten Blick scheint es, dass der 3. Fall anzuwenden ist:
- a = 8, b = 2, f(n) = n3ln(n)
- Für den 3. Fall ist zu zeigen:
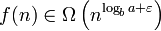
- Definition vom Ω-Kalkül:
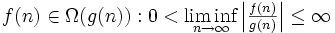
- Angewandt auf
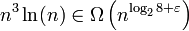 :
: 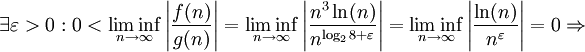 Widerspruch!
Widerspruch!- Es existiert kein
 , sodass der Limes ungleich Null ist. Also ist der 3. Fall nicht auf diese Rekursionsgleichung anwendbar!
, sodass der Limes ungleich Null ist. Also ist der 3. Fall nicht auf diese Rekursionsgleichung anwendbar!
Es gilt: 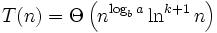 , falls
, falls 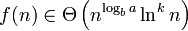
Genau betrachtet stellt diese Formel eine Verallgemeinerung des zweiten Falls dar.
Lösung nach obiger Formel: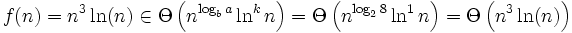 √
√- Da f(n) die notwendige Bedingung erfüllt, gilt nun:
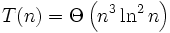
- Siehe zu demselben Beispiel auch die Aufwandsabschätzung im Ο-Kalkül mit Hilfe der Substitutionsmethode.
Bemerkungen
- Angenommen es ist folgende Rekurrenz gegeben, die sich mit der zusätzlichen Konstante c von der allgemeinen Form unterscheidet.
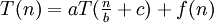
- Wenn n hinreichend groß gewählt wird, fällt die Konstante c nicht ins Gewicht. Aus diesem Grund kann man solche Rekurrenzen so behandeln, als wäre c = 0.
- Angenommen es ist folgende Rekurrenz gegeben, bei der n / b durch die Floor- oder Ceiling-Funktion angegeben werden:
- z. B.:
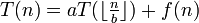
- In diesem Fall kann man
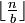 oder auch
oder auch 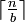 als
als 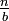 interpretieren.
interpretieren.
- Ob man nun
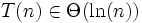 (Logarithmus naturalis) schreibt, oder
(Logarithmus naturalis) schreibt, oder 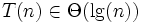 (dekadischer Logarithmus) ist egal, da nach den Logarithmengesetzen gilt:
(dekadischer Logarithmus) ist egal, da nach den Logarithmengesetzen gilt:
Allgemeinere Form
In allgemeinerer Form gilt auch
Definition
Sei
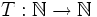 die zu untersuchende Abbildung der Form
die zu untersuchende Abbildung der Form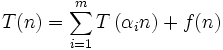 ,
,
wobei
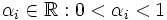 ,
, 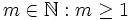 und
und 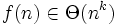 mit
mit 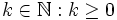 .
.T wird hierfür implizit durch
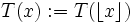 oder
oder 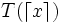 für
für 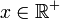 auf die reellen Zahlen fortgesetzt.
auf die reellen Zahlen fortgesetzt.Dann gilt:
Literatur
- Th.H.Cormen/C.E.Leiserson/R.Rivest/C.Stein: Algorithmen - Eine Einführung. Oldenbourg Verlag 2004. ISBN 3-486-27515-1
- Th.E.Cormen/C.E.Leiserson/R.Rivest/C.Stein: Introduction to Algorithms. MIT Press 2002 ISBN 0-262-03293-7
Siehe auch
Wikimedia Foundation.