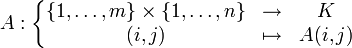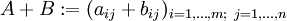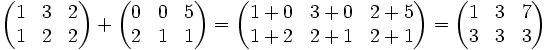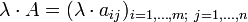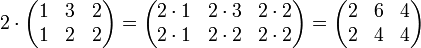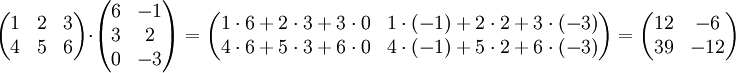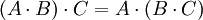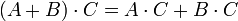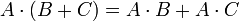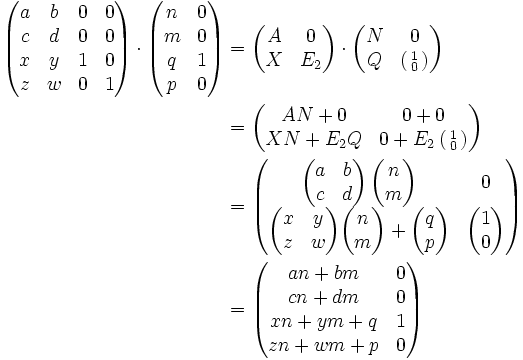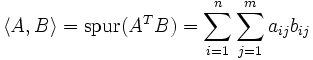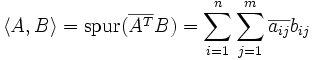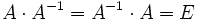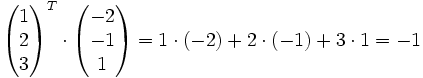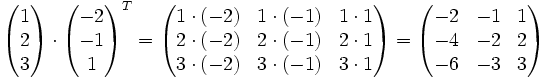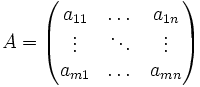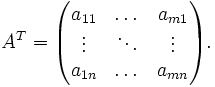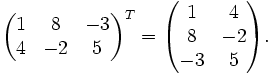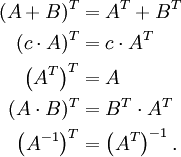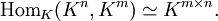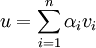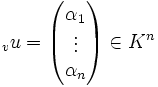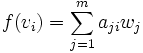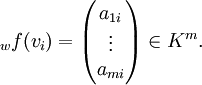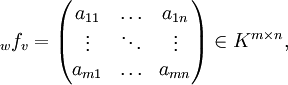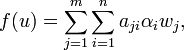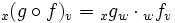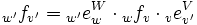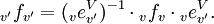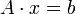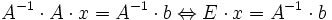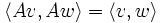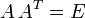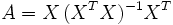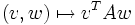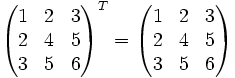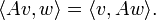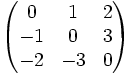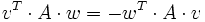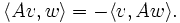- Matrizenprodukt
-
In der Mathematik ist eine Matrix (Plural: Matrizen) eine Tabelle von Zahlen oder anderen Größen, die addiert und multipliziert werden können. Matrizen unterscheiden sich von einfachen Tabellen dadurch, dass mit ihnen gerechnet werden kann. Wenn Matrizen von der Größe her zusammenpassen, ist es möglich, sie zu addieren oder miteinander zu multiplizieren.
Matrizen sind ein Schlüsselkonzept der linearen Algebra. Sie werden unter anderem dazu benutzt, lineare Gleichungssysteme zu beschreiben und lineare Abbildungen darzustellen.
Man spricht von den Zeilen und Spalten einer Matrix; diese bilden Zeilenvektoren und Spaltenvektoren. Die Elemente, die in einer Matrix angeordnet sind, nennt man Einträge oder Komponenten der Matrix.
Die Bezeichnung „Matrix“ wurde 1850 von James Joseph Sylvester eingeführt. Matrizen stellen Zusammenhänge, in denen insbesondere Linearkombinationen eine Rolle spielen, übersichtlich dar und erleichtern damit Rechen- und Gedankenvorgänge.
Inhaltsverzeichnis
Notation und erste Eigenschaften
Als Notation hat sich die Aneinanderreihung der Elemente in Zeilen und Spalten mit einer großen öffnenden und schließenden Klammer durchgesetzt. Die Form der Klammern ist nicht festgelegt; es werden sowohl runde als auch eckige Klammern verwendet. Beispielhaft stehen die Notationen
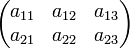 und
und 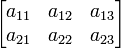
für eine Matrix mit zwei Zeilen und drei Spalten. Allgemein spricht man von einer
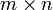 -Matrix mit m Zeilen und n Spalten. Deshalb nennt man auch m die Zeilendimension und n die Spaltendimension der Matrix.
-Matrix mit m Zeilen und n Spalten. Deshalb nennt man auch m die Zeilendimension und n die Spaltendimension der Matrix.Die Einträge der Matrix entstammen einer Menge K. In der linearen Algebra ist diese in der Regel ein Körper; meistens verwendet man die reellen oder komplexen Zahlen. Man spricht in diesem Fall von einer reellen Matrix oder einer Matrix über
 bzw. von einer komplexen Matrix oder einer Matrix über
bzw. von einer komplexen Matrix oder einer Matrix über  . In der Algebra werden oft Matrizen mit Einträgen aus einem Ring betrachtet.
. In der Algebra werden oft Matrizen mit Einträgen aus einem Ring betrachtet.Formal kann eine Matrix als eine Familie bzw. als eine Funktion
aufgefasst werden, die jedem Indexpaar (i,j) einen Funktionswert A(i,j) zuordnet. In den obigen Beispielmatrizen wird beispielsweise dem Indexpaar (1,2) der Funktionswert A(1,2) = a12 zugeordnet. Allgemein ist der Funktionswert A(i,j) der Eintrag in der i-ten Zeile und der j-ten Spalte. Die Indizes m und n entsprechen wieder der Anzahl der Zeilen bzw. Spalten. Nicht zu verwechseln mit dieser formalen Definition einer Matrix durch Funktionen ist, dass Matrizen selbst lineare Abbildungen beschreiben.
Die Menge
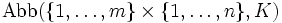 aller
aller 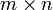 -Matrizen über der Menge K wird in üblicher mathematischer Notation auch
-Matrizen über der Menge K wird in üblicher mathematischer Notation auch 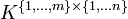 geschrieben; hierfür hat sich die Kurznotation
geschrieben; hierfür hat sich die Kurznotation 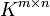 eingebürgert (manchmal werden auch die Schreibweisen Km,n,
eingebürgert (manchmal werden auch die Schreibweisen Km,n, 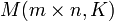 , oder seltener
, oder seltener 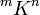 benutzt).
benutzt).Stimmen Zeilen- und Spaltenanzahl überein, so spricht man von einer quadratischen Matrix.
Hat eine Matrix nur eine Spalte, so nennt man sie einen Spaltenvektor; hat sie nur eine Zeile, so nennt man sie einen Zeilenvektor. Einen Vektor aus Kn kann man je nach Kontext als einzeilige oder einspaltige Matrix darstellen (also als Element aus
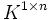 oder
oder 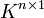 ).
).Addition und Multiplikation
Matrizenaddition
Die Summe zweier
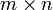 -Matrizen berechnet sich, indem man jeweils die Einträge der beiden Matrizen addiert:
-Matrizen berechnet sich, indem man jeweils die Einträge der beiden Matrizen addiert:Rechenbeispiel:
Es können nur Matrizen mit der gleichen Anzahl an Zeilen und der gleichen Anzahl an Spalten addiert werden.
In der linearen Algebra sind die Einträge der Matrizen üblicherweise Elemente eines Körpers, wie z. B. der reellen oder komplexen Zahlen. In diesem Fall ist die Matrizenaddition assoziativ, kommutativ und besitzt mit der Nullmatrix ein neutrales Element. Im Allgemeinen besitzt die Matrizenaddition diese Eigenschaften jedoch nur, wenn die Einträge Elemente einer algebraischen Struktur sind, die diese Eigenschaften hat.
Skalarmultiplikation
Eine Matrix wird mit einem Skalar multipliziert, indem alle Einträge der Matrix mit dem Skalar multipliziert werden:
Rechenbeispiel:
Die Skalarmultiplikation darf nicht mit dem Skalarprodukt verwechselt werden. Um die Skalarmultiplikation durchführen zu dürfen, müssen der Skalar λ und die Einträge der Matrix demselben Ring
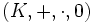 entstammen. Die Menge der
entstammen. Die Menge der 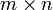 -Matrizen ist in diesem Fall ein K-(Links-)Modul über K.
-Matrizen ist in diesem Fall ein K-(Links-)Modul über K.Matrizenmultiplikation
Zwei Matrizen
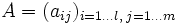 und
und 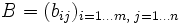 werden multipliziert, indem die Produktsummenformel, ähnlich dem Skalarprodukt, auf Paare aus einem Zeilenvektor der ersten und einem Spaltenvektor der zweiten Matrix angewandt wird:
werden multipliziert, indem die Produktsummenformel, ähnlich dem Skalarprodukt, auf Paare aus einem Zeilenvektor der ersten und einem Spaltenvektor der zweiten Matrix angewandt wird: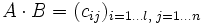 und
und 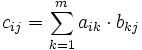
Rechenbeispiel:
Bei der Berechnung von Hand bietet das falksche Schema eine Hilfestellung. Bei der Berechnung mit dem Computer kann sich bei großen Matrizen der Einsatz des Strassen-Algorithmus lohnen.
Damit zwei Matrizen multipliziert werden können, müssen die Einträge einem Ring entstammen und die Spaltenanzahl der linken mit der Zeilenanzahl der rechten Matrix übereinstimmen. Ist nun A eine
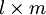 -Matrix und B eine
-Matrix und B eine 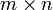 -Matrix dann ist
-Matrix dann ist 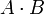 eine
eine 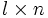 -Matrix.
-Matrix.Zu beachten ist, dass Matrizenmultiplikation im Allgemeinen nicht kommutativ ist, d. h. im Allgemeinen gilt
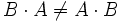 , sofern überhaupt beide Seiten sinnvoll sind, was mit den Annahmen im letzten Absatz bedeutet, dass l = n gilt. Ist diese Bedingung erfüllt, dann sind beide Seiten quadratische Matrizen; diese sind aber nur "gleich groß" (d.h. haben gleich viele Zeilen - und Spalten), wenn außerdem m = n ist. Auch bei l = m = n sind aber die beiden Produkte im Allgemeinen verschieden.
, sofern überhaupt beide Seiten sinnvoll sind, was mit den Annahmen im letzten Absatz bedeutet, dass l = n gilt. Ist diese Bedingung erfüllt, dann sind beide Seiten quadratische Matrizen; diese sind aber nur "gleich groß" (d.h. haben gleich viele Zeilen - und Spalten), wenn außerdem m = n ist. Auch bei l = m = n sind aber die beiden Produkte im Allgemeinen verschieden.Die Matrizenmultiplikation ist aber immer assoziativ:
Die Matrixaddition und Matrixmultiplikation genügen zudem den beiden Distributivgesetzen:
für alle
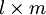 -Matrizen A,B und
-Matrizen A,B und 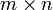 -Matrizen C sowie
-Matrizen C sowiefür alle
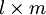 -Matrizen A und
-Matrizen A und 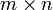 -Matrizen B,C.
-Matrizen B,C.Eine besondere Rolle bezüglich der Matrizenmultiplikation spielen die quadratischen Matrizen über einem Ring R, also
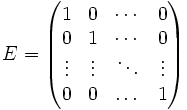
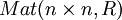 . Diese bilden selbst mit der Matrizenaddition und -multiplikation wiederum einen Ring. Ist der Ring R unitär mit dem Eins-Element 1, dann ist die Einheitsmatrix
. Diese bilden selbst mit der Matrizenaddition und -multiplikation wiederum einen Ring. Ist der Ring R unitär mit dem Eins-Element 1, dann ist die Einheitsmatrixdas Eins-Element des Matrizenrings, d. h. dieser ist auch unitär. Allerdings ist der Matrizenring
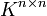 für n > 1 niemals kommutativ.
für n > 1 niemals kommutativ.Zerlegt man Matrizen in Blockmatrizen, so können diese komponentenweise ausmultipliziert werden:
Hierbei ist E2 die
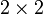 -Einheitsmatrix. Mit 0 ist die jeweils passende Matrix gemeint, deren Komponenten alle 0 sind.
-Einheitsmatrix. Mit 0 ist die jeweils passende Matrix gemeint, deren Komponenten alle 0 sind.Potenzieren von Matrizen
Quadratische Matrizen
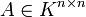 können mit sich selbst multipliziert werden; analog zur Potenz bei den reellen Zahlen führt man abkürzend die Matrixpotenz
können mit sich selbst multipliziert werden; analog zur Potenz bei den reellen Zahlen führt man abkürzend die Matrixpotenz 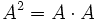 oder
oder 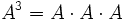 etc. ein. Damit ist es auch sinnvoll, quadratische Matrizen als Elemente in Polynomen einzusetzen. Zu weitergehenden Ausführungen hierzu siehe unter charakteristisches Polynom. Zur einfacheren Berechnung kann hier die jordansche Normalform verwendet werden.
etc. ein. Damit ist es auch sinnvoll, quadratische Matrizen als Elemente in Polynomen einzusetzen. Zu weitergehenden Ausführungen hierzu siehe unter charakteristisches Polynom. Zur einfacheren Berechnung kann hier die jordansche Normalform verwendet werden.Quadratische Matrizen über
 oder
oder  kann man darüber hinaus sogar in Potenzreihen einsetzen, vgl. Matrixexponential.
kann man darüber hinaus sogar in Potenzreihen einsetzen, vgl. Matrixexponential.Vektorräume von Matrizen
Die
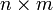 -Matrizen über einem kommutativen Ring R mit 1 bilden mit der Matrizenaddition und der Skalarmultiplikation jeweils einen R-Modul. Die Spur des Matrixprodukts
-Matrizen über einem kommutativen Ring R mit 1 bilden mit der Matrizenaddition und der Skalarmultiplikation jeweils einen R-Modul. Die Spur des Matrixprodukts 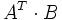
ist dann ein Skalarprodukt auf dem Matrizenraum.
Im Spezialfall
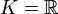 handelt es sich bei diesem Matrizenraum um einen euklidischen Vektorraum. In diesem Raum stehen die symmetrischen Matrizen und die schiefsymmetrischen Matrizen senkrecht aufeinander. Ist A eine symmetrische und B eine schiefsymmetrische Matrix, so gilt
handelt es sich bei diesem Matrizenraum um einen euklidischen Vektorraum. In diesem Raum stehen die symmetrischen Matrizen und die schiefsymmetrischen Matrizen senkrecht aufeinander. Ist A eine symmetrische und B eine schiefsymmetrische Matrix, so gilt 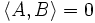 .
.Im Spezialfall
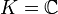 ist die Spur des Matrixproduktes
ist die Spur des Matrixproduktes 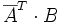
ein Skalarprodukt, das Hilbert-Schmidt-Skalarprodukt, und der Matrizenraum wird zu einem unitären Vektorraum.
Weitere Rechenoperationen
Inverse Matrix
Hauptartikel: Inverse Matrix
Für manche quadratische Matrizen A gibt es eine Matrix A − 1, für die
gilt, wobei E die Einheitsmatrix ist. A − 1 heißt inverse Matrix von A. Matrizen, die eine inverse Matrix besitzen, bezeichnet man als invertierbare oder reguläre Matrizen. Umgekehrt werden nicht-invertierbare Matrizen als singuläre Matrizen bezeichnet.
Vektor-Vektor-Produkte (Skalarprodukt und Tensorprodukt)
Hat man zwei Spaltenvektoren v und w der Länge n, dann ist das Matrixprodukt
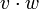 nicht definiert, aber die beiden Produkte
nicht definiert, aber die beiden Produkte 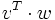 und
und 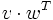 existieren.
existieren.Das erste Produkt ist eine
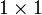 -Matrix, die als Zahl interpretiert wird, sie wird das kanonische Skalarprodukt von v und w genannt und mit
-Matrix, die als Zahl interpretiert wird, sie wird das kanonische Skalarprodukt von v und w genannt und mit 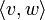 bezeichnet.
bezeichnet.Das zweite Produkt ist eine
 -Matrix (vom Rang 1) und heißt das dyadische Produkt oder Tensorprodukt von v und w.
-Matrix (vom Rang 1) und heißt das dyadische Produkt oder Tensorprodukt von v und w.Die transponierte Matrix
Die Transponierte der Matrix
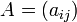 vom Format
vom Format 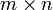 ist die Matrix
ist die Matrix 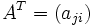 vom Format
vom Format 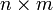 , d.h., zu
, d.h., zuist die Transponierte
Man schreibt also die erste Zeile als erste Spalte und die zweite Zeile als zweite Spalte usw. Die Matrix wird sozusagen an ihrer Hauptdiagonale (
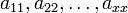 mit
mit 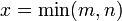 ) gespiegelt.
) gespiegelt.Beispiel:
Es gelten die folgenden Rechenregeln:
Die transponierte Matrix wird gelegentlich auch gestürzte Matrix genannt.
Bei Matrizen über
 ist die adjungierte Matrix genau die transponierte Matrix.
ist die adjungierte Matrix genau die transponierte Matrix.Anwendungen
Zusammenhang mit linearen Abbildungen
Das Besondere an Matrizen über einem Ring K ist der Zusammenhang zu linearen Abbildungen. Zu jeder Matrix
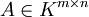 lässt sich eine lineare Abbildung mit Definitionsbereich Kn (Menge der Spaltenvektoren) und Wertebereich Km definieren, indem man jeden Spaltenvektor
lässt sich eine lineare Abbildung mit Definitionsbereich Kn (Menge der Spaltenvektoren) und Wertebereich Km definieren, indem man jeden Spaltenvektor 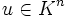 auf
auf 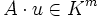 abbildet; und jede lineare Abbildung mit diesem Definitions- und Wertebereich entspricht auf diese Weise genau einer
abbildet; und jede lineare Abbildung mit diesem Definitions- und Wertebereich entspricht auf diese Weise genau einer 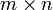 -Matrix. Diesen Zusammenhang bezeichnet man auch als (kanonischen) Isomorphismus
-Matrix. Diesen Zusammenhang bezeichnet man auch als (kanonischen) IsomorphismusEr stellt bei vorgegebenem K, m, n eine Bijektion zwischen der Menge der Matrizen und der Menge der linearen Abbildungen dar. Das Matrixprodukt geht hierbei über in die Komposition (Hintereinanderausführung) linearer Abbildungen. Weil die Klammerung bei der Hintereinanderausführung dreier linearer Abbildungen keine Rolle spielt, gilt dies dann auch für die Matrixmultiplikation, sie ist also assoziativ.
Ist K sogar ein Körper, kann man statt der Spaltenvektorräume beliebige endlichdimensionale K-Vektorräume V und W (der Dimension n bzw. m) betrachten. (Falls K ein kommtutativer Ring mit 1 ist, dann kann man analog freie K-Moduln betrachten.) Diese sind nach Wahl von Basen
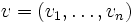 von V und
von V und 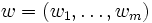 von W zu Kn bzw. Km isomorph, weil zu einem beliebigen Vektor
von W zu Kn bzw. Km isomorph, weil zu einem beliebigen Vektor 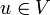 eine eindeutige Zerlegung in Basisvektoren
eine eindeutige Zerlegung in Basisvektorenexistiert und die darin vorkommenden Körperelemente αi den Koordinatenvektor
bilden. Jedoch hängt der Koordinatenvektor von der verwendeten Basis v ab, die daher auch in der Bezeichnung vu vorkommt.
Analog verhält es sich im Vektorraum W. Ist eine lineare Abbildung
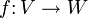 gegeben, so lassen sich die Bilder der Basisvektoren von V eindeutig in die Basisvektoren von W zerlegen in der Form
gegeben, so lassen sich die Bilder der Basisvektoren von V eindeutig in die Basisvektoren von W zerlegen in der Formmit Koordinatenvektor
Die Abbildung ist dann vollständig festgelegt durch die sog. Abbildungsmatrix
denn für das Bild des o.g. Vektors u gilt
also
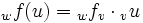 („Koordinatenvektor = Matrix mal Koordinatenvektor“). (Die Matrix wfv hängt von den verwendeten Basen v und w ab; bei der Multiplikation wird die Basis v, die links und rechts vom Malpunkt steht, „weggekürzt“, und die „außen“ stehende Basis w bleibt übrig.)
(„Koordinatenvektor = Matrix mal Koordinatenvektor“). (Die Matrix wfv hängt von den verwendeten Basen v und w ab; bei der Multiplikation wird die Basis v, die links und rechts vom Malpunkt steht, „weggekürzt“, und die „außen“ stehende Basis w bleibt übrig.)Die Hintereinanderausführung zweier linearer Abbildungen
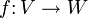 und
und 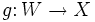 (mit Basen v, w bzw. x) entspricht dabei der Matrixmultiplikation, also
(mit Basen v, w bzw. x) entspricht dabei der Matrixmultiplikation, also(auch hier wird die Basis w „weggekürzt“).
Somit ist die Menge der linearen Abbildungen von V nach W wieder isomorph zu
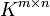 . Der Isomorphismus
. Der Isomorphismus 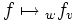 hängt aber von den gewählten Basen v und w ab und ist daher nicht kanonisch: Bei Wahl einer anderen Basis v' für V bzw. w' für W wird derselben linearen Abbildung nämlich eine andere Matrix zugeordnet, die aus der alten durch Multiplikation von rechts bzw. links mit einer nur von den beteiligten Basen abhängigen invertierbaren
hängt aber von den gewählten Basen v und w ab und ist daher nicht kanonisch: Bei Wahl einer anderen Basis v' für V bzw. w' für W wird derselben linearen Abbildung nämlich eine andere Matrix zugeordnet, die aus der alten durch Multiplikation von rechts bzw. links mit einer nur von den beteiligten Basen abhängigen invertierbaren 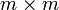 - bzw.
- bzw.  -Matrix (sog. Basiswechselmatrix) entsteht. Das folgt durch zweimalige Anwendung der Multiplikationsregel aus dem vorigen Absatz, nämlich
-Matrix (sog. Basiswechselmatrix) entsteht. Das folgt durch zweimalige Anwendung der Multiplikationsregel aus dem vorigen Absatz, nämlich(„Matrix = Basiswechselmatrix mal Matrix mal Basiswechselmatrix“). Dabei bilden die Identitätsabbildungen eV und eW jeden Vektor aus V bzw. W auf sich selbst ab.
Bleibt eine Eigenschaft von Matrizen unberührt von solchen Basiswechseln, so ist es sinnvoll, diese Eigenschaft auch basisunabhängig der entsprechenden linearen Abbildung zuzusprechen.
Im Zusammenhang mit Matrizen oft auftretende Begriffe sind der Rang und die Determinante einer Matrix. Der Rang ist (falls K ein Körper ist) im angeführten Sinne basisunabhängig, und man kann somit vom Rang auch bei linearen Abbildungen sprechen. Die Determinante ist nur für quadratische Matrizen definiert, die dem Fall V = W entsprechen; sie bleibt unverändert, wenn derselbe Basiswechsel im Definitions- und Wertebereich durchgeführt wird, wobei beide Basiswechselmatrizen zueinander invers sind:
In diesem Sinne ist also auch die Determinante basisunabhängig.
Umformen von Matrizengleichungen
Speziell in den multivariaten Verfahren werden häufig Beweisführungen, Herleitungen usw. im Matrizenkalkül durchgeführt.
Gleichungen werden im Prinzip wie algebraische Gleichungen umgeformt, wobei jedoch die Nichtkommutativität der Matrixmultiplikation sowie die Existenz von Nullteilern beachtet werden muss.
Beispiel: Lineares Gleichungssystem als einfache Umformung
Gesucht ist der Lösungsvektor x eines linearen Gleichungssystems
mit A als
 -Koeffizientenmatrix. Wenn die inverse Matrix A − 1 existiert, kann man mit ihr von links erweitern:
-Koeffizientenmatrix. Wenn die inverse Matrix A − 1 existiert, kann man mit ihr von links erweitern:und erhält die Lösung
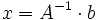 .
.
Siehe auch weitere Anwendungen.
Spezielle Matrizen
Eigenschaften von Endomorphismen
Die folgenden Eigenschaften quadratischer Matrizen entsprechen Eigenschaften von Endomorphismen, die durch sie dargestellt werden.
- Orthogonale Matrizen
- Eine reelle Matrix A ist orthogonal, wenn die zugehörige lineare Abbildung das Standard-Skalarprodukt erhält, d.h. wenn
- gilt. Diese Bedingung ist äquivalent dazu, dass A die Gleichung
- A − 1 = AT
- bzw.
- erfüllt.
- Diese Matrizen stellen Spiegelungen, Drehungen und Drehspiegelungen dar.
- Unitäre Matrizen
- Sie sind das komplexe Gegenstück zu den orthogonalen Matrizen. Eine komplexe Matrix A ist unitär, wenn die zugehörige Transformation die Normierung erhält, d.h. wenn
- gilt. Diese Bedingung ist äquivalent dazu, dass A die Gleichung
- A − 1 = A *
- erfüllt; dabei bezeichnet A * die konjugiert-transponierte Matrix zu A.
- Fasst man den n-dimensionalen komplexen Vektorraum als 2n-dimensionalen reellen Vektorraum auf, so entsprechen die unitären Matrizen genau denjenigen orthogonalen Matrizen, die mit der Multiplikation mit i vertauschen.
- Projektionsmatrizen
- Eine Matrix ist eine Projektionsmatrix, falls
- A = A2
- gilt, sie also idempotent ist, d.h., die mehrfache Anwendung einer Projektionsmatrix auf einen Vektor lässt das Resultat unverändert. Eine idempotente Matrix hat keinen vollen Rang, es sei denn, sie ist die Einheitsmatrix.
- Beispiel: Es sei X eine
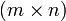 -Matrix, und damit selbst nicht invertierbar. Dann ist die
-Matrix, und damit selbst nicht invertierbar. Dann ist die 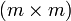 -Matrix
-Matrix
- idempotent. Diese Matrix wird beispielsweise in der Methode der kleinsten Quadrate verwendet.
- Geometrisch entsprechen Projektionsmatrizen der Parallelprojektion entlang des Nullraumes der Matrix.
- Nilpotente Matrizen
- Eine Matrix N heißt nilpotent, falls eine Potenz Nk (und damit auch alle höheren Potenzen) die Nullmatrix ergibt.
Eigenschaften von Bilinearformen
Im folgenden sind Eigenschaften von Matrizen aufgelistet, die Eigenschaften der zugehörigen Bilinearform
entsprechen. Trotzdem können diese Eigenschaften auch für die dargestellten Endomorphismen eine eigenständige Bedeutung besitzen.
- Symmetrische Matrizen
- Eine Matrix A heißt symmetrisch, wenn sie gleich ihrer transponierten Matrix ist:
- AT = A
- Anschaulich gesprochen sind die Einträge symmetrischer Matrizen symmetrisch zur Hauptdiagonalen.
- Beispiel:
- Symmetrische Matrizen entsprechen einerseits symmetrischen Bilinearformen:
- vTAw = wTAv,
- andererseits den selbstadjungierten linearen Abbildungen:
- Hermitesche Matrizen
- Hermitesche Matrizen sind das komplexe Analogon der symmetrischen Matrizen. Sie entsprechen den hermiteschen Sesquilinearformen und den selbstadjungierten Endomorphismen.
- Eine Matrix
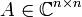 ist hermitesch oder selbstadjungiert, wenn gilt:
ist hermitesch oder selbstadjungiert, wenn gilt:
- A = A * .
- Schiefsymmetrische Matrizen
- Eine Matrix A heißt schiefsymmetrisch oder auch antisymmetrisch, wenn gilt:
- − AT = A.
- Um diese Bedingung zu erfüllen muss die Hauptdiagonale in allen Stellen null sein; die restlichen Werte werden über die Hauptdiagonale gespiegelt und negiert.
- Beispiel:
- Schiefsymmetrische Matrizen entsprechen antisymmetrischen Bilinearformen:
- und antiselbstadjungierten Endomorphismen:
- Positiv definite Matrizen
- Eine reelle Matrix ist positiv definit, wenn die zugehörige Bilinearform positiv definit ist, d.h. wenn für alle Vektoren
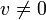 gilt:
gilt:
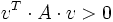 .
.
- Positiv definite Matrizen definieren verallgemeinerte Skalarprodukte. Ist die Bilinearform größer gleich Null, heißt die Matrix positiv semidefinit, analog kann eine Matrix negativ definit beziehungsweise semidefinit heißen, wenn die obige Bilinearform immer kleiner beziehungsweise kleiner gleich Null ist. Matrizen, die keine dieser Eigenschaften erfüllen, heißen indefinit.
Weitere Konstruktionen
- Konjugierte und Adjungierte Matrix
- Enthält eine Matrix komplexe Zahlen, erhält man die konjugierte Matrix, indem man ihre Komponenten durch die konjugiert komplexen Elemente ersetzt. Die adjungierte Matrix (auch hermitesch konjugierte Matrix) einer Matrix A wird mit A * bezeichnet und entspricht der transponierten Matrix, bei der zusätzlich alle Elemente komplex konjugiert werden. Manchmal wird auch die komplementäre Matrix
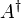 als adjungierte bezeichnet.
als adjungierte bezeichnet.
- Adjunkte oder Komplementäre Matrix
- Die komplementäre Matrix
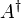 einer quadratischen Matrix A setzt sich aus deren Unterdeterminanten zusammen, wobei eine Unterdeterminante auch Minor genannt wird. Für die Ermittlung der Unterdeterminanten det(Aij) werden die i-te Zeile und j-te Spalte von A gestrichen. Aus der resultierenden
einer quadratischen Matrix A setzt sich aus deren Unterdeterminanten zusammen, wobei eine Unterdeterminante auch Minor genannt wird. Für die Ermittlung der Unterdeterminanten det(Aij) werden die i-te Zeile und j-te Spalte von A gestrichen. Aus der resultierenden 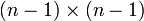 -Matrix wird dann die Determinante det(Aij) berechnet. Die komplementäre Matrix hat dann die Einträge ( − 1)i + jdet(Aji). Diese Matrix wird manchmal auch als Matrix der Kofaktoren bezeichnet.
-Matrix wird dann die Determinante det(Aij) berechnet. Die komplementäre Matrix hat dann die Einträge ( − 1)i + jdet(Aji). Diese Matrix wird manchmal auch als Matrix der Kofaktoren bezeichnet.
- Man verwendet die komplementäre Matrix beispielsweise zur Berechnung der Inversen einer Matrix A, denn nach dem laplaceschen Entwicklungssatz gilt
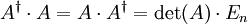 .
.
- Damit ist die Inverse
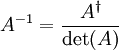 , wenn
, wenn  .
.
Verallgemeinerungen
Man könnte auch Matrizen mit unendlich vielen Spalten oder Zeilen betrachten. Diese kann man immer noch addieren. Um sie jedoch multiplizieren zu können, muss man zusätzliche Bedingungen an ihre Komponenten stellen (da die auftretenden Summen unendliche Reihen sind und nicht konvergieren müssen). Die genaueren Betrachtungen solcher Fragestellungen führten zur Entstehung der Funktionalanalysis, die diese Begriffe behandelt.
Werden analog zu den Matrizen mathematische Strukturen mit mehr als zwei Indizes definiert, so nennt man diese Tensoren.
Weblinks
- The Matrix Cookbook – Eine englischsprachige, umfangreiche Matrix-Formelsammlung (PDF)
Wikimedia Foundation.