- Basiswechsel (Vektorraum)
-
Der Basiswechsel oder die Basistransformation ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra. Man bezeichnet damit den Übergang zwischen zwei verschiedenen Basen eines endlichdimensionalen Vektorraums über einem Körper K. Dadurch ändern sich im Allgemeinen die Koordinaten der Vektoren und die Abbildungsmatrizen von linearen Abbildungen. Ein Basiswechsel ist somit ein Spezialfall einer Koordinatentransformation.
Der Basiswechsel kann durch eine Matrix beschrieben werden, die Basiswechselmatrix oder Transformationsmatrix genannt wird. Mit dieser lassen sich auch die Koordinaten bezüglich der neuen Basis ausrechnen. Stellt man die Basisvektoren der alten Basis als Linearkombinationen der Vektoren der neuen Basis dar, so bilden die Koeffizienten dieser Linearkombinationen die Einträge der Basiswechselmatrix.
Inhaltsverzeichnis
Basiswechselmatrix
Es sei V ein n-dimensionaler Vektorraum über dem Körper K (zum Beispiel dem Körper
 der reellen Zahlen). In V seien zwei geordnete Basen gegeben,
der reellen Zahlen). In V seien zwei geordnete Basen gegeben,  und
und  mit Basisvektoren
mit Basisvektoren  bzw.
bzw.  . Die Basiswechselmatrix
. Die Basiswechselmatrix  für den Basiswechsel von B nach B' ist eine
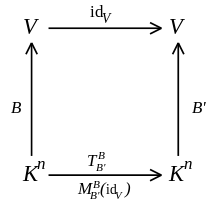
für den Basiswechsel von B nach B' ist eine  -Matrix. Es handelt sich um die Abbildungsmatrix der Identitätsabbildung auf V bezüglich der Basen B im Urbild und B' im Bild:
-Matrix. Es handelt sich um die Abbildungsmatrix der Identitätsabbildung auf V bezüglich der Basen B im Urbild und B' im Bild:Man erhält sie, indem man die Vektoren der alten Basis B als Linearkombinationen der Vektoren der neuen Basis B' darstellt:
Die Koeffizienten
 bilden die j-te Spalte der Basiswechselmatrix
bilden die j-te Spalte der BasiswechselmatrixDiese Matrix ist quadratisch und invertierbar und somit ein Element der allgemeinen linearen Gruppe
 . Ihre Inverse
. Ihre Inverse  beschreibt den Basiswechsel von B' zurück nach B.
beschreibt den Basiswechsel von B' zurück nach B.Koordinatentransformation
Ein Vektor
 habe bezüglich der Basis
habe bezüglich der Basis  die Koordinaten
die Koordinaten  , d. h.
, d. h.und bezüglich der neuen Basis
 die Koordinaten
die Koordinaten  , also
, alsoStellt man wie oben die Vektoren bj der alten Basis als Linearkombination der neuen Basis dar, so erhält man
Dabei sind die aij die oben definierten Einträge der Basiswechselmatrix
 . Durch Koeffizientenvergleich erhält man
. Durch Koeffizientenvergleich erhält manbzw. in Matrizenschreibweise:
oder kurz:
Basiswechsel bei Abbildungsmatrizen
Die Darstellungsmatrix einer linearen Abbildung hängt von der Wahl der Basen im Urbild- und im Zielraum ab. Wählt man andere Basen, so erhält man auch andere Abbildungsmatrizen.
Seien V ein n-dimensionaler und W ein m-dimensionaler Vektorraum über K und
 eine lineare Abbildung. In V seien die geordneten Basen
eine lineare Abbildung. In V seien die geordneten Basen  und
und  gegeben, in W die geordneten Basen
gegeben, in W die geordneten Basen  und
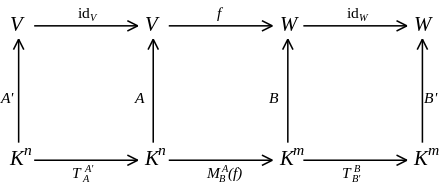
und  . Dann gilt für die Darstellungsmatrizen von f bezüglich A und B bzw. bezüglich A' und B':
. Dann gilt für die Darstellungsmatrizen von f bezüglich A und B bzw. bezüglich A' und B':Man erhält diese Darstellung, indem man
schreibt. Die Abbildungsmatrix der Verkettung ist dann das Matrizenprodukt der einzelnen Abbildungsmatrizen, wenn die Basen passend gewählt sind, das heißt: die Basis A' im Urbild von
 , die Basis A im Bild von
, die Basis A im Bild von  und im Urbild von f, die Basis B im Bild von f und im Urbild von
und im Urbild von f, die Basis B im Bild von f und im Urbild von  , und die Basis B' im Bild von
, und die Basis B' im Bild von  . Man erhält also:
. Man erhält also:Ein wichtiger Spezialfall ist, wenn
 ein Endomorphismus ist und im Urbild und Bild jeweils dieselbe Basis B bzw. B' benutzt wird. Dann gilt:
ein Endomorphismus ist und im Urbild und Bild jeweils dieselbe Basis B bzw. B' benutzt wird. Dann gilt:Setzt man
 , so gilt also
, so gilt alsoDie Abbildungsmatrizen
 und
und  sind also ähnlich.
sind also ähnlich.Anwendung
Basiswechselmatrizen besitzen vielfältige Anwendungsmöglichkeiten in der Mathematik und Physik.
In der Mathematik
Eine Anwendung von Basiswechselmatrizen in der Mathematik ist die Veränderung der Gestalt der Abbildungsmatrix einer linearen Abbildung um die Rechnung zu vereinfachen.
Betrachtet man beispielsweise eine beliebige diagonalisierbare
 -Matrix A. Möchte man nun
-Matrix A. Möchte man nun  berechnen, so benötigt die direkte Berechnung
berechnen, so benötigt die direkte Berechnung  Körpermultiplikationen. Da A diagonalisierbar ist existieren eine Diagonalmatrix D und eine Basiswechselmatrix
Körpermultiplikationen. Da A diagonalisierbar ist existieren eine Diagonalmatrix D und eine Basiswechselmatrix  sodass
sodassDie Berechnung der rechten Seite benötigt hingegen nur
 Körpermultiplikationen.
Körpermultiplikationen.Beispiel
Wir betrachten zwei Basen B und C des
 :
:wobei die Koordinatendarstellung der Vektoren die Vektoren bezüglich der Standardbasis beschreibt.
Die Abbildung eines Vektors
- v = β1b1 + β2b2 + β3b3 = γ1c1 + γ2c2 + γ3c3
ergibt sich durch die Darstellung der alten Basisvektoren (b1,b2,b3) bezüglich der neuen Basis (c1,c2,c3) und deren Gewichtung mit (β1,β2,β3).
Um die Matrix der Basistransformation
 von B nach C zu berechnen, müssen wir die drei linearen Gleichungssysteme
von B nach C zu berechnen, müssen wir die drei linearen Gleichungssysteme- bi = T1ic1 + T2ic2 + T3ic3
nach den 9 Unbekannten Tji auflösen.
Dies kann mit dem Gauß-Jordan-Algorithmus für alle 3 Gleichungssysteme simultan erfolgen. Dazu wird folgendes LGS aufgestellt:
Durch Umformen mit elementaren Zeilenoperationen lässt sich die linke Seite auf die Einheitsmatrix bringen und auf der rechten Seite erhält man die Matrix
 .
.
Wir betrachten einen Vektor v, der bezüglich der Standardbasis die Koordinatendarstellung (5,2,7) besitzt. Bezüglich B ist
 .
.
Das Subskript bezeichne die zur Koordinatendarstellung gehörige Basis. Um nun die Koordinatendarstellung bezüglich C zu berechnen, müssen wir die Transformationsmatrix auf diesen Spaltenvektor anwenden:
 .
.
Also ist
 .
.
In der Physik
Eine Anwendung von Basiswechselmatrizen in der Physik findet bspw. in der Ähnlichkeitstheorie statt, um dimensionslose Kennzahlen zu ermitteln. Hierbei werden durch einen Basiswechsel einer physikalischen Größe neue Basisdimensionen zugeordnet. Die dimensionslosen Kennzahlen stellen dann genau das Verhältnis der physikalischen Größe zu seiner Dimensionsvorschrift dar.
Beispiel
Wir betrachten die Viskosität
 dargestellt durch seine Basisdimensionen: Länge l, Masse m und Zeit t. Es gilt:
dargestellt durch seine Basisdimensionen: Länge l, Masse m und Zeit t. Es gilt: .
.Es sei also nun die Basis B eine Exponentendarstellung der Basisdimensionen die
 bilden:
bilden:Die Exponenteneinträge lauten dann für den Vektor mB:
 .
.
Als neue Basis C wählen wir die bestimmenden Parameter einer Strömung: Dichte , Anströmgeschwindigkeit U und die charakteristische Länge L. Diese Basisvektoren lassen sich aus ihrer Dimensionsvorschrift aus den Basisvektoren (b1,b2,b3) herleiten. So lautet die neue Basis C nun:
, Anströmgeschwindigkeit U und die charakteristische Länge L. Diese Basisvektoren lassen sich aus ihrer Dimensionsvorschrift aus den Basisvektoren (b1,b2,b3) herleiten. So lautet die neue Basis C nun:Um die Matrix der Basistransformation
 von B nach C zu berechnen, müssen analog zum vorherigen Beispiel die drei linearen Gleichungssysteme nach den 9 Unbekannten Tji aufgelöst werden.
von B nach C zu berechnen, müssen analog zum vorherigen Beispiel die drei linearen Gleichungssysteme nach den 9 Unbekannten Tji aufgelöst werden.Es ergibt sich:

und somit für den Vektor
 mit den neuen Basisvektoren:
mit den neuen Basisvektoren: .
.Durch die neuen Dimensionen gilt nun die Proportionalität:
 .
.Das Verhältnis hiervon liefert die dimensionslose Reynoldszahl:
 .
.Literatur
- Gerd Fischer: Lineare Algebra: Eine Einführung für Studienanfänger. 13 Auflage. Vieweg, 2002, ISBN 3-528-97217-3.
- Prandtl/Oswatitsch/Wieghardt, Führer durch die Strömungslehre, 7. Aufl., Braunschweig 1969
Weblink
Wikimedia Foundation.










 auf
auf  abbildet, etc.
abbildet, etc.










