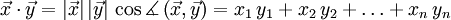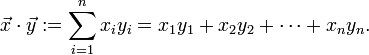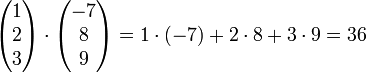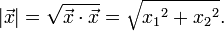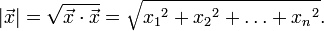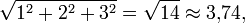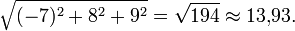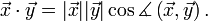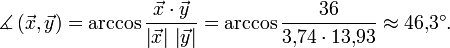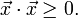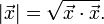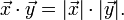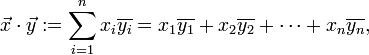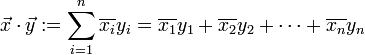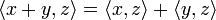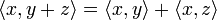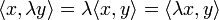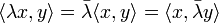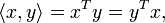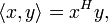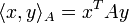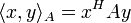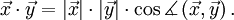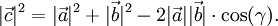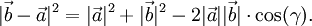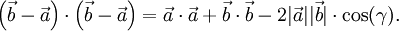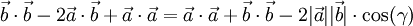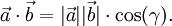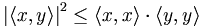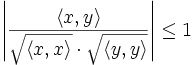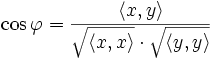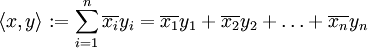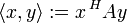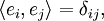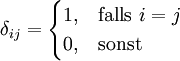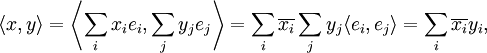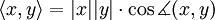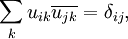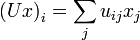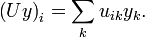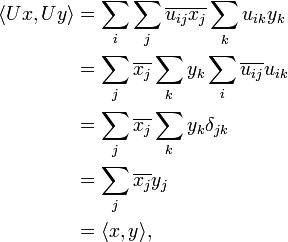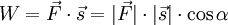- Summenprodukt
-
Das Skalarprodukt (auch inneres Produkt oder Punktprodukt) ist eine mathematische Verknüpfung. Historisch wurde es zuerst für den euklidischen Raum eingeführt. Dort berechnet sich das Skalarprodukt zweier Vektoren
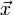 und
und 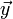 nach der Formel
nach der FormelDabei sind
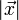 und
und 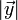 jeweils die Längen der Vektoren. Mit
jeweils die Längen der Vektoren. Mit 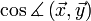 wird der Kosinus des Winkels zwischen den beiden Vektoren bezeichnet. Wie bei der normalen Multiplikation wird das Multiplikationszeichen auch ganz weggelassen:
wird der Kosinus des Winkels zwischen den beiden Vektoren bezeichnet. Wie bei der normalen Multiplikation wird das Multiplikationszeichen auch ganz weggelassen: 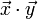 =
= 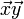 .
.Es gibt eine weitere einfache Methode das Skalarprodukt zu berechnen, und zwar durch komponentenweises Multiplizieren der Koordinaten der Vektoren und anschließendes Aufsummieren. Diese Berechnungsmethode für das Skalarprodukt wird oft verwendet, um Winkel zwischen zwei Vektoren und die Länge von Vektoren zu bestimmen.
In der Linearen Algebra, einem Teilgebiet der Mathematik, wird dieses Konzept verallgemeinert. Ein Skalarprodukt ist dort eine Funktion, die zwei Elementen eines Vektorraums ein Element des dem Vektorraum zugrunde liegenden Skalarkörpers zuordnet. Als Notation verwendet man dann
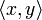 für das Skalarprodukt zweier Vektoren x und y. Ist die Bedeutung von x und y klar, lässt man die spitzen Klammern auch weg und schreibt xy. Auch die Notation xTy ist gebräuchlich, zeigt sie doch die enge Verwandtschaft zur Matrizenmultiplikation auf.
für das Skalarprodukt zweier Vektoren x und y. Ist die Bedeutung von x und y klar, lässt man die spitzen Klammern auch weg und schreibt xy. Auch die Notation xTy ist gebräuchlich, zeigt sie doch die enge Verwandtschaft zur Matrizenmultiplikation auf.Im Allgemeinen gibt es auf reellen oder komplexen Vektorräumen mehrere Skalarprodukte, ein Raum zusammen mit einem Skalarprodukt wird als Innenproduktraum oder Prähilbertraum bezeichnet. Diese verallgemeinern den euklidischen Raum und ermöglichen damit die Anwendung geometrischer Methoden auf abstrakte Strukturen.
Das Skalarprodukt darf nicht mit der Skalarmultiplikation verwechselt werden. Hierbei wird ein Vektor mit einem Skalar des Vektorraums multipliziert, meistens also einer reellen oder komplexen Zahl.
Definition im endlichdimensionalen euklidischen Raum (kanonisches Skalarprodukt oder Standardskalarprodukt)
In der linearen Algebra ist das Standardskalarprodukt oder innere Produkt zweier Vektoren
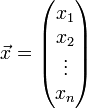 und
und 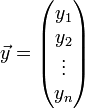
des n-dimensionalen euklidischen Raumes als die Summe der Produkte der Komponenten der Vektoren definiert:
Im dreidimensionalen euklidischen Raum berechnet man also das Skalarprodukt von zwei Spaltenvektoren zum Beispiel als
Betrag von Vektoren
Mit Hilfe des Skalarproduktes ist es möglich, die Länge (den Betrag) eines Vektors zu berechnen:
Für Vektoren des zweidimensionalen Raumes ergibt die Länge wegen des rechtwinkligen Dreiecks nach dem Satz des Pythagoras:
Dies kann man mit demselben Satz für beliebige Dimensionen erweitern:
Die Längen der beiden Spaltenvektoren im obenstehenden Beispiel betragen also
Winkelberechnung
Im euklidischen Raum gilt die Formel aus der Einleitung (eine Begründung für diese Formel findet sich weiter unten)
Damit lässt sich der Winkel zwischen den Vektoren im obenstehenden Beispiel berechnen:
Grundlegende Eigenschaften
Es gilt
Deswegen ist
immer reell.
Sind zwei Vektoren
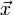 und
und 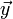 parallel, so gilt
parallel, so giltStehen zwei Vektoren
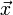 und
und 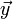 aufeinander senkrecht (orthogonal), so gilt
aufeinander senkrecht (orthogonal), so gilt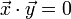 .
.
Damit lässt sich auf einfache Weise überprüfen, ob zwei Vektoren zueinander orthogonal sind.
Ist einer der beiden Vektoren ein Einheitsvektor, so ergibt das Skalarprodukt die Länge der Projektion des anderen Vektors auf die vom Einheitsvektor definierte Gerade.
Definition des Standardskalarproduktes im komplexen Vektorraum
Man definiert im Fall des komplexen Vektorraums
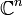 über dem Körper
über dem Körper  das Standardskalarprodukt für alle
das Standardskalarprodukt für alle 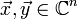 folgendermaßen:
folgendermaßen:wobei der Überstrich die komplexe Konjugation bedeutet. Alternativ könnte man auch
definieren. Beide Definitionen sind gleichwertig, denn das eine Skalarprodukt ist die komplexe Konjugation des anderen. In der Praxis ist es aber zweckmäßig, sich auf eine einzige Definition zu einigen, wobei in der Mathematik die Version
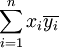 bevorzugt wird, in der Physik hingegen die Version
bevorzugt wird, in der Physik hingegen die Version 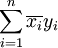 . Für beide Definitionen gilt
. Für beide Definitionen gilt 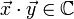 und wie im Reellen
und wie im Reellen 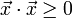 , da aufgrund der Definition
, da aufgrund der Definition 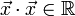 ist und im Gegensatz zu
ist und im Gegensatz zu  auf
auf  die Ordnungsrelation
die Ordnungsrelation 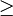 definiert ist.
definiert ist.Eigenschaften
- Während das Skalarprodukt im reellen Fall symmetrisch ist, d.h. es gilt
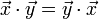 , ist es im komplexen Fall hermitesch, was
, ist es im komplexen Fall hermitesch, was 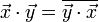 bedeutet.
bedeutet. - Das Skalarprodukt ist nicht assoziativ (und kann es im eigentlichen Sinne auch gar nicht sein, weil sein Wert ein Skalar und nicht wieder ein Vektor ist).
- Das Skalarprodukt ist distributiv bezüglich der Addition und Subtraktion.
- Es gilt:
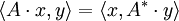 , wobei A * die zu A adjungierte Matrix ist.
, wobei A * die zu A adjungierte Matrix ist.
Allgemeine Definition
In der allgemeinen Theorie werden die Variablen für Vektoren, also Elemente eines beliebigen Vektorraums, im Allgemeinen nicht durch Pfeile gekennzeichnet. Das Skalarprodukt wird meist nicht durch einen Malpunkt, sondern durch ein Paar von spitzen Klammern bezeichnet.
- Ein Skalarprodukt oder inneres Produkt auf einem reellen Vektorraum V ist eine symmetrische positiv definite Bilinearform
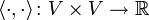 , d.h. für
, d.h. für 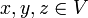 und
und 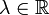 gelten die folgenden Bedingungen:
gelten die folgenden Bedingungen:
- bilinear:
- symmetrisch:
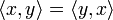
- positiv definit:
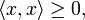 und
und 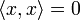 genau dann, wenn x = 0
genau dann, wenn x = 0
- bilinear:
- Ein Skalarprodukt oder inneres Produkt auf einem komplexen Vektorraum V ist eine hermitesche positiv definite Sesquilinearform
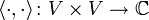 , d.h. für
, d.h. für 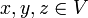 und
und 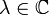 gelten die folgenden Bedingungen:
gelten die folgenden Bedingungen:
- sesquilinear:
- hermitesch:
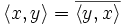
- positiv definit:
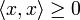 , und
, und 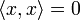 genau dann, wenn x = 0. (Dass
genau dann, wenn x = 0. (Dass 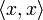 reell ist, folgt aus Bedingung 2.)
reell ist, folgt aus Bedingung 2.)
- sesquilinear:
Ein reeller oder komplexer Vektorraum, in dem ein inneres Produkt definiert ist, heißt Innenproduktraum oder Prähilbertraum; ist er darüber hinaus auch noch vollständig bezüglich der durch das innere Produkt induzierten Norm, wird er als Hilbertraum bezeichnet.
Abweichende Definitionen:
- Oft wird jede symmetrische Bilinearform bzw. jede hermitesche Sesquilinearform als Skalarprodukt bezeichnet; mit diesem Sprachgebrauch beschreiben die obigen Definitionen positiv definite Skalarprodukte.
- Im komplexen Fall ließe sich das Skalarprodukt alternativ als semilinear im zweiten und linear im ersten Argument definieren. In der Physik wird jedoch die obige Variante durchgängig benutzt (siehe Bra- und Ket-Vektoren). Siehe hierzu auch den Abschnitt „Standardskalarprodukt als Matrizenprodukt“ weiter unten.
Skalarprodukt als Matrizenprodukt
Das Standardskalarprodukt lässt sich auch als Matrizenprodukt schreiben, indem man den Vektor als
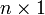 -Matrix (Spaltenvektor) interpretiert: Im reellen Fall gilt
-Matrix (Spaltenvektor) interpretiert: Im reellen Fall giltwobei T für die transponierte Matrix steht.
Im komplexen Fall gilt (für den links semilinearen, rechts linearen Fall)
wobei H für die hermitesch adjungierte Matrix steht.
Allgemeiner definiert im reellen Fall jede symmetrische und positiv definite Matrix A über
ein Skalarprodukt; ebenso wird im komplexen Fall für jede hermitesch und positiv definite Matrix A über
ein Skalarprodukt definiert.
Skalarprodukt und Winkel
Winkelberechnung im euklidischen Raum
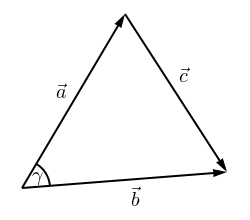
Das Skalarprodukt ist ursprünglich im Rahmen der analytischen Geometrie im euklidischen Raum eingeführt worden. So ist es mit Hilfe des Skalarproduktes beispielsweise möglich, den Winkel zwischen zwei Vektoren zu berechnen: Das Skalarprodukt ergibt sich nämlich auch aus den Beträgen der beiden Vektoren und dem Kosinus des von diesen eingeschlossenen Winkels gemäß der Formel
Um dies zu zeigen, mögen drei Vektoren,
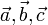 des euklidischen Raumes betrachtet werden.
des euklidischen Raumes betrachtet werden.Wegen des Kosinussatzes ist die Länge des dem Winkel γ gegenüberliegenden Vektors
Da sich
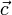 als
als 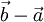 ergibt, erhält man
ergibt, erhält manBerechnet man nun die Länge über das Skalarprodukt, so erhält man
Aus den Rechenregeln für das Skalarprodukt ergibt sich dann
und daraus die gewünschte Beziehung
Skalarprodukt und Orthogonalität
Aus der Winkeldarstellung des Skalarprodukts folgt, dass das Skalarprodukt zweier von Null verschiedener Vektoren genau dann Null ist, wenn der Kosinus des von ihnen eingeschlossenen Winkels Null ist, wenn also die beiden Vektoren zueinander orthogonal sind.
Winkeldefinition im abstrakten Fall
Die Cauchy-Schwarzsche Ungleichung besagt, dass für das abstrakte Skalarprodukt die Beziehung
gilt, die im Falle
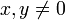 zu
zuumgeformt werden kann. Daher lässt sich auch im abstrakten Fall mittels
der Winkel
 zweier Vektoren definieren.
zweier Vektoren definieren.Berechnung des Skalarprodukts mit Hilfe seiner Komponenten
In einem endlichdimensionalen Vektorraum ist das in der Einleitung definierte Skalarprodukt
nicht die einzige Funktion, die der abstrakten Definition des inneren Produkts entspricht. So genügt beispielsweise auch die Funktion
für jede positiv definite, hermitesche Matrix A der abstrakten Definition eines inneren Produkts. Umgekehrt, jedes gegebene innere Produkt lässt sich mit Hilfe solch einer Matrix darstellen, dies ist also die allgemeine Form eines inneren Produkts auf dem komplexen Vektorraum
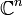 . Lässt sich nun aber zu einem gegebenen inneren Produkt eine Orthonormalbasis finden, also eine Menge von Vektoren
. Lässt sich nun aber zu einem gegebenen inneren Produkt eine Orthonormalbasis finden, also eine Menge von Vektoren 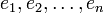 mit
mitwobei
das Kronecker-Delta darstellt, und kann man
in dieser Basis darstellen, so erhält man aus den Rechenregeln des inneren Produktes
also genau die in der Einleitung definierte Berechnung des Skalarprodukts mit Hilfe der Komponenten der beiden Vektoren x und y. Im endlichdimensionalen Fall lässt sich zeigen, dass es stets möglich ist, eine solche Orthonormalbasis zu finden, beispielsweise über die Gram-Schmidt-Orthogonalisierung.
Der Begriff der Orthonormalbasis und die Berechnung des inneren Produkts mit Hilfe der Komponenten der beiden Argumente lassen sich auf unendlichdimensionale Räume verallgemeinern, wobei die Vektoren üblicherweise nur als eine unendliche Summe von Vektoren aus der Orthonormalbasis dargestellt werden können und das innere Produkt daher ebenfalls eine unendliche Summe wird. Die Orthonormalbasis ist also keine Basis im Sinne der linearen Algebra, die eine Darstellung jedes Vektors als endliche Summe von Basisvektoren ermöglicht. Zur besseren Unterscheidung wird daher im unendlichdimensionalen Fall die Basis im Sinne der linearen Algebra als Hamelbasis bezeichnet.
Skalarprodukt und unitäre Transformationen
Aus der Darstellung des Skalarprodukts mittels Winkel
folgt geometrisch, dass das Skalarprodukt invariant gegenüber längen- und winkeltreuen Abbildungen sein muss. Dies lässt sich auch analytisch nachrechnen. Längen- und winkeltreue Abbildungen werden durch unitäre Matrizen U dargestellt, das sind Matrizen mit der Eigenschaft UUH = I oder
wobei δij das Kronecker-Delta darstellt. Für die i-te Komponente von Ux und Uy gilt
und
Somit berechnet sich das Skalarprodukt als
das Skalarprodukt bleibt also tatsächlich unverändert.
Anwendung
In der Physik sind viele Größen, wie zum Beispiel die Arbeit W, durch Skalarprodukte definiert:
mit den vektoriellen Größen Kraft F und Weg s.
Literatur
- Gerd Fischer: Lineare Algebra. 15. Auflage. Vieweg Verlag, ISBN 3528032170.
Siehe auch
- Skalarmultiplikation (S-Multiplikation)
- Kreuzprodukt
- Ausartungsraum
Weblinks
Einzelnachweise
Wikimedia Foundation.