Maximalgrad

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Nachbarschaft und Grad sind grundlegende Begriffe der Graphentheorie, einem Teilgebiet der Mathematik. Sie beschreiben Eigenschaften von Knoten.

Definitionen

Nachbarschaft

Ungerichtete Graphen

Zwei Knoten u und v heißen in einem ungerichteten Graphen G benachbart, verbunden oder adjazent, wenn sie durch eine ungerichtete Kante verbunden sind.
Ein Knoten v und eine ungerichtete Kante e heißen inzident, wenn e den Knoten v mit einem anderen Knoten verbindet (v ist Element von e). Zwei ungerichtete Kanten heißen benachbart, wenn sie nicht disjunkt sind, d.h. wenn sie einen gemeinsamen Knoten besitzen.

Ein Knoten x heißt Nachbar eines Knotens y in einem ungerichteten Graphen G, wenn x und y zu einer Kante von G gehören. Mit N_G(v) bezeichnet man die Menge aller Nachbarn eines Knotens v in G. Ferner bezeichnet man mit N_G(X) die Menge aller Nachbarn der Knoten von X in G. N_G(v) bzw. N_G(X) nennt man auch Nachbarschaft von v bzw. X.

Ein Knoten ist sein eigener Nachbar, wenn er eine Schlinge besitzt. Die Nachbarschaft einer Menge von Knoten N_G(X) kann Knoten aus der Menge X selbst enthalten. Die Vereinigung der Nachbarschaft mit den Knoten aus X heißt abgeschlossene Nachbarschaft.

Diese Begriffe gelten analog für Hypergraphen und -kanten.

Gerichtete Graphen

Ein Knoten x heißt Vorgänger von y in einem gerichteten Graphen G, wenn (x, y) gerichtete Kante von G ist. Mit N_G^-(v) bezeichnet man die Menge aller Vorgänger eines Knotens v in G. Ferner bezeichnet man mit N_G^-(X) die Menge aller Vorgänger der Knoten von X in G. N_G^-(v) bzw. N_G^-(X) nennt man auch Vorgängermenge oder Eingangsmenge von v bzw. X.

Analog heißt x Nachfolger von y in G, wenn (y, x) gerichtete Kante von G ist. Mit N_G⁺(v) bezeichnet man die Menge aller Nachfolger eines Knotens v in G. Ferner bezeichnet man mit N_G⁺(X) die Menge aller Nachfolger der Knoten von X in G. N_G⁺(v) bzw. N_G⁺(X) nennt man auch Nachfolgermenge oder Ausgangsmenge von v bzw. X.

Grad

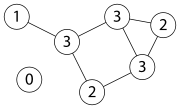
Der Grad (oder Valenz) d_G(v) in einem Graphen ist der Anzahl Kanten, die den Knoten v mit einem anderen Knoten verbinden. Oft wird auch die Notation deg_G(v) (engl. degree) verwendet

Falls klar ist, um welchen Graphen es sich handelt, lässt man den Index G bei N, N^-, N⁺, d, d^- und d⁺ auch oft weg.

Ungerichtete Graphen

Ein ungerichteter Graph. Die Knoten sind mit ihrem Grad beschriftet.

In einem ungerichteten Graph ist d_G(v) in

• Graphen ohne Mehrfachkanten und Hypergraphen die Anzahl der Nachbarn von v,
• Graphen mit Mehrfachkanten die Summe der Vielfachheiten aller mit v inzidenten Kanten.

Den kleinsten Grad eines Knotens in G bezeichnet man dann als Minimalgrad von G, den größten Grad eines Knotens in G bezeichnet man als Maximalgrad von G. Das arithmetische Mittel aller Eckengrade von G wird als Durchschnittsgrad d_G(G) bezeichnet.

Gerichtete Graphen

Ein gerichteter Graph mit beschrifteten Knoten: (Eingangsgrad, Ausgangsgrad)

In gerichteten Graphen wird unterschieden, ob eine Kante an einem Knoten beginnt oder endet. Mit d_G^-(v) bezeichnet man den Eingangsgrad des Knotens v in einem gerichteten Graphen G und mit d_G⁺(v) dessen Ausgangsgrad.

Dabei ist d_G^-(v) in

• Graphen ohne Mehrfachkanten die Anzahl der Vorgänger von v,
• Graphen mit Mehrfachkanten die Summe der Vielfachheiten aller Kanten in G der Form (v, x).

und d_G⁺(v) in

• Graphen ohne Mehrfachkanten die Anzahl der Nachfolger von v,
• Graphen mit Mehrfachkanten die Summe der Vielfachheiten aller Kanten in G der Form (x, v).

Einen Knoten ohne Eingangskanten (d_G^-(v) = 0) nennt man Quelle, einen Knoten ohne Ausgangskanten (d_G⁺(v) = 0) nennt man Senke.

Spezialfälle und -begriffe

• Man nennt einen Knoten isoliert, wenn er:
  • in einem ungerichteten Graphen: keine Nachbarn besitzt d_G = 0.
  • in einem gerichteten Graphen: keine Vorgänger und keine Nachfolger besitzt. $d_G^+ = d_G^- =0$.

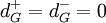• Ein ungerichteter Graph (bzw. Hypergraph) G heißt regulär, falls alle seine Knoten denselben Grad besitzen. Besitzen alle seine Knoten Grad k, so bezeichnet man G als k-regulär. Einen 3-regulären Graphen bezeichnet man auch als kubisch.

• Ein gerichteter Graph G heißt regulär, falls alle seine Knoten denselben Eingangs- und Ausgangsgrad besitzen. Besitzen alle seine Knoten Eingangs- und Ausgangsgrad k, so bezeichnet man G als k-regulär.

• Ein Hypergraph G heißt uniform, wenn alle Kanten von G die gleiche Anzahl Knoten enthalten. Enthalten alle Kanten von G genau k Knoten, so nennt man G k-uniform.