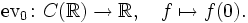- Maximalideal
-
Maximales Ideal ist ein Begriff aus der Algebra.
Definition
Es sei R ein Ring. Dann heißt ein Ideal
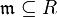 maximal, wenn
maximal, wenn 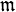 ein maximales Element ist in der durch die (mengentheoretische) Inklusion
ein maximales Element ist in der durch die (mengentheoretische) Inklusion 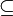 (teilweise) geordneten Menge aller echten Ideale. D.h.
(teilweise) geordneten Menge aller echten Ideale. D.h. 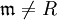 und für jedes Ideal
und für jedes Ideal 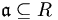 gilt:
gilt:- Aus
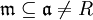 folgt
folgt 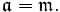
In anderen Worten:
Ein Ideal
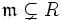 ist maximal, wenn es nicht echte Teilmenge eines echten (vom ganzen Ring verschiedenen) Ideals von R ist.
ist maximal, wenn es nicht echte Teilmenge eines echten (vom ganzen Ring verschiedenen) Ideals von R ist.Bemerkungen
- Entsprechendes gilt jeweils für Links- bzw. Rechtsideale.
- Mit Hilfe des Zornschen Lemmas kann man zeigen, dass jedes echte Ideal in einem Ring mit Einselement 1 in einem maximalen Ideal enthalten ist.
- Daraus folgt wiederum, dass jedes Element eines Ringes mit 1, das keine Einheit ist, in einem maximalen Ideal enthalten sein muss.
- Ringe können mehrere maximale Ideale enthalten. Ein (noetherscher) Ring, der nur ein einziges maximales Links- oder Rechtsideal besitzt, wird als lokaler Ring bezeichnet.
- Sei
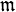 ein Ideal des kommutativen Ringes R mit 1. Der Faktorring
ein Ideal des kommutativen Ringes R mit 1. Der Faktorring 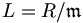 ist genau dann ein Körper, wenn
ist genau dann ein Körper, wenn 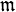 maximal ist. Insbesondere heißt dies: Das Bild eines Ringhomomorphismus ist genau dann ein Körper, wenn dessen Kern maximal ist.
maximal ist. Insbesondere heißt dies: Das Bild eines Ringhomomorphismus ist genau dann ein Körper, wenn dessen Kern maximal ist. - Ein maximales (zweiseitiges) Ideal
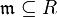 eines Ringes R ist genau dann prim, wenn
eines Ringes R ist genau dann prim, wenn 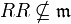 . Insbesondere ist
. Insbesondere ist 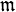 prim, falls R ein Einselement enthält.
prim, falls R ein Einselement enthält.
Beispiele
- Im Ring
 der ganzen Zahlen ist jedes Primideal außer dem Nullideal maximal. Dies ist jedoch im Allgemeinen nicht richtig; Integritätsbereiche mit dieser Eigenschaft heißen eindimensional. In einem Hauptidealring gilt dieser Satz ebenfalls.
der ganzen Zahlen ist jedes Primideal außer dem Nullideal maximal. Dies ist jedoch im Allgemeinen nicht richtig; Integritätsbereiche mit dieser Eigenschaft heißen eindimensional. In einem Hauptidealring gilt dieser Satz ebenfalls. - Sei
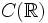 der Ring der stetigen Funktionen auf den reellen Zahlen mit der punktweisen Multiplikation. Betrachte den Ringhomomorphismus
der Ring der stetigen Funktionen auf den reellen Zahlen mit der punktweisen Multiplikation. Betrachte den Ringhomomorphismus
-
- Mit anderen Worten: diejenige Abbildung die jede Funktion an der Stelle 0 auswertet. Das Bild von ev0 ist
 , also ein Körper. Somit ist der Kern, also die Menge aller Funktionen mit f(0) = 0, ein maximales Ideal.
, also ein Körper. Somit ist der Kern, also die Menge aller Funktionen mit f(0) = 0, ein maximales Ideal.
- Aus
Wikimedia Foundation.