Maximierungsproblem

Bei einem Optimierungsproblem ist ein Lösungsraum (Menge von möglichen Lösungen) Ω und eine Bewertungsfunktion (auch Ziel- oder Fitnessfunktion) 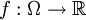$f: \Omega \rightarrow \mathbb{R}$ gegeben. Man will eine Lösung 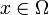$x \in \Omega$ mit möglichst großem Wert f(x) finden, oder Aussagen über die Werte der Lösungen machen.

In diesem Fall läge ein Maximierungsproblem vor, bei einem Minimierungsproblem sind Lösungen x mit möglichst kleinem f(x) gesucht, aber dieser Fall lässt sich durch einfaches Negieren von f auf den vorigen zurückführen.

Man unterscheidet drei Problemstellungen:

• Entscheidungsprobleme, bei denen zusätzlich ein Grenzwert 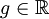$g \in \mathbb{R}$ gegeben ist, und ermittelt werden soll, ob es ein 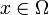$x \in \Omega$ gibt mit $f(x) \geq g$.
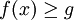• eigentliche Optimierungsprobleme, bei denen man den Wert der besten Lösung wissen will, also $\max \{f(x) | x \in \Omega\}$.
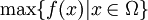• Suchprobleme, bei denen eine optimale Lösung 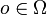$o \in \Omega$ gesucht ist, also so dass 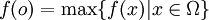$f(o) = \max \{f(x) | x \in \Omega\}$. Zumindest will man eine möglichst gute Lösung finden, falls das Ermitteln einer optimalen Lösung nicht praktikabel ist (Approximation).

In der Theoretischen Informatik meint man mit Optimierungsproblem in der Regel ein eigentliches Optimierungsproblem, bei dem also nur der bestmögliche Wert und keine Lösung selbst gesucht ist. Auch betrachtet man üblicherweise den Sonderfall einer diskreten Bewertungsfunktion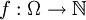 $f: \Omega \rightarrow \mathbb{N}$, da dies meist keinen erheblichen Unterschied macht und man reelle Zahlen bzw. Gleitkommazahlen weniger gut handhaben kann.

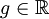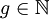Meistens betrachtet man in der Theoretischen Informatik aber Entscheidungsprobleme. Zu einem Optimierungsproblem lässt sich leicht ein Entscheidungsproblem erzeugen, indem man zur Problemstellung den Grenzwert $g \in \mathbb{R}$ bzw. $g \in \mathbb{N}$ hinzunimmt.

In der praktischen Anwendung hat man es meistens mit Suchproblemen zu tun, denn der Wert einer optimalen Lösung nützt einem ohne Kenntnis dieser Lösung in der Regel nichts. Einen Algorithmus, der ein Optimierungsproblem löst, nennt man Optimierungsalgorithmus. Analog spricht man beim Minimierungs- und Maximierungsproblem genauer vom Minimierungs- oder Maximierungsalgorithmus. Einen Algorithmus, der ein Optimierungsproblem näherungsweise löst, nennt man Approximationsalgorithmus.

Siehe auch Optimierung (Mathematik), Evolutionärer Algorithmus