- Mengenkörper
-
Als Mengenalgebra (auch Mengenkörper, Teilmengenverband oder oft auch kurz Algebra), bezeichnet man ein Mengensystem, das bezüglich Komplementbildung und Vereinigung abgeschlossen ist (Ereignissystem). Auch das Teilgebiet der Mathematik, das vom Rechnen mit Mengen handelt, wird als Mengenalgebra bezeichnet. Ähnliche doppeldeutig ist auch der Begriff Algebra, der für ein Teilgebiet der Mathematik und auch für eine spezielle mathematische Struktur benutzt wird.
Inhaltsverzeichnis
Formale Definition
Jede Mengenalgebra
 ist Teilmenge der Potenzmenge
ist Teilmenge der Potenzmenge 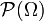 einer Grundmenge Ω. Folgende Axiome müssen gelten:
einer Grundmenge Ω. Folgende Axiome müssen gelten: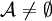 (
( ist nicht leer);
ist nicht leer);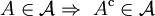 (Mit jeder Menge A enthält
(Mit jeder Menge A enthält  auch das Komplement
auch das Komplement 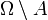 );
);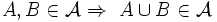 (Mit jeden zwei Mengen A, B enthält
(Mit jeden zwei Mengen A, B enthält  auch deren Vereinigung
auch deren Vereinigung 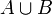 .)
.)
Eigenschaften
Da
 nicht leer ist, enthält es gewiss irgendeine Menge A und somit auch
nicht leer ist, enthält es gewiss irgendeine Menge A und somit auch 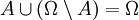 sowie
sowie 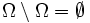 .
.Aus den Axiomen folgt, dass
 auch abgeschlossen bezüglich der Schnittmengenbildung sowie der Differenzmengenbildung ist. Man kann auch umgekehrt die Abgeschlossenheit unter Schnittmengenbildung axiomatisch fordern und daraus auf die Abgeschlossenheit unter Vereinigung schließen.
auch abgeschlossen bezüglich der Schnittmengenbildung sowie der Differenzmengenbildung ist. Man kann auch umgekehrt die Abgeschlossenheit unter Schnittmengenbildung axiomatisch fordern und daraus auf die Abgeschlossenheit unter Vereinigung schließen.Eine Mengenalgebra bildet ein Monoid (
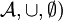 mit der Vereinigung als innerer Verknüpfung und der Nullmenge als neutralem Element. Sie bildet ein weiteres Monoid
mit der Vereinigung als innerer Verknüpfung und der Nullmenge als neutralem Element. Sie bildet ein weiteres Monoid 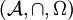 mit dem Schnitt als Verknüpfung und der Grundmenge als neutralem Element.
mit dem Schnitt als Verknüpfung und der Grundmenge als neutralem Element.Aufgrund der Existenz eines Komplements bildet eine Mengenalgebra überdies einen distributiven Verband.
Verwandte Strukturen
Wenn man Axiom (3) verschärft und die Abgeschlossenheit auch gegenüber der Vereinigung abzählbar unendlich vieler Mengen fordert, erhält man die Definition einer σ-Algebra.
Schwächt man die Definition ab, indem man anstelle von (2) die Abgeschlossenheit bezüglich Differenz fordert, so erhält man die Definition eines Mengenrings. Eine weitere Abschwächung liefert die Definition des Mengenhalbrings. Es gilt somit, dass jede Algebra ein Ring bzw. Halbring ist.
Jede Mengenalgebra ist eine boolesche Algebra.
Siehe auch
Literatur
- Heinz Bauer: Maß- und Integrationstheorie, Walter de Gruyter, Berlin - New York 1992, ISBN 3-11-013626-0
- Elstrodt: Maß- und Integrationstheorie. ISBN 3-540-65420-8
- Ernst Henze: Einführung in die Maßtheorie. ISBN 3-411-03102-6
Wikimedia Foundation.
