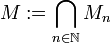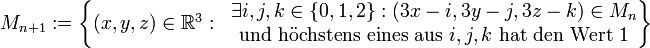Mengerscher Schwamm

Der Menger-Schwamm (nach Karl Menger benannt) gehört wie das Sierpinski-Dreieck und die Koch-Kurve zu den Objekten der fraktalen Geometrie. Der Mengersche Schwamm ist ein dreidimensionales Analogon der Cantor-Menge oder des Sierpinski-Teppichs: aus einem Quadrat wird in der Mitte ein Neuntel der Fläche des Quadrats entfernt. Aus den von dem Quadrat um das Loch verbliebenen acht quadratischen Feldern wird wiederum je ein Neuntel der Fläche entfernt, und so weiter.

Sierpinski-Teppich:
Stufe 0	Stufe 1	Stufe 2	Stufe 3	Stufe 4	Stufe 5

Wenn man den Sierpinski-Teppich nun auf einen Würfel überträgt, dann bekommt man ein Gebilde, das einem Schwamm nicht unähnlich ist. In jedem Iterationsschritt wird der Würfel (bzw. jeder der Teilwürfel) in 27 (3*3*3) Teilwürfel zerlegt und 7 dieser Teilwürfel werden entfernt.

Das Volumen des Schwammes konvergiert dabei gegen 0, während die Oberfläche gegen unendlich strebt. Anders formuliert, besitzt der „Körper“ des Menger-Schwamms eine Hausdorff-Dimension kleiner als 3 (im Gegensatz zu nicht-fraktalen, tatsächlich 3-dimensionalen Körpern), während gleichzeitig seine Oberfläche eine Hausdorff-Dimension größer als 2 besitzt (im Gegensatz zur 2-dimensionalen Oberfläche nicht-fraktaler Körper). Der genaue Wert der Hausdorff-Dimension des Menger-Schwamms ist $\ln 20/\ln 3 = 2.726833\ldots$ .

Formale Definition

Formal lässt sich ein Menger-Schwamm M auf folgende Weise definieren:

$M := \bigcap_{n\in\mathbb{N}} M_n$

wobei M₀ den Einheitswürfel bezeichne und

$M_{n+1} := \left\{\begin{matrix} (x,y,z)\in\mathbb{R}^3: & \begin{matrix}\exists i,j,k\in\{0,1,2\}: (3x-i,3y-j,3z-k)\in M_n \\ \mathrm{und\ h \ddot o chstens\ eines\ aus\ }i,j,k\mbox{ hat den Wert 1}\end{matrix} \end{matrix}\right\}$

Bilder

Würfel

1. Iteration

2. Iteration

3. Iteration

4. Iteration

5. Iteration

Modell eines Mengerschwamms in der 4. Iterationsstufe. Hergestellt mit einem 3D-Drucker von Z-Corporation durch Dr. Daniel Lordick, Institut für Geometrie, TU Dresden, Dez. 2004

Weblinks

• Menger Sponge -- from MathWorld (engl.)
• Institut für Visualisierung und Interaktive Systeme - Menger-Schwamm