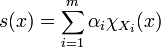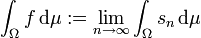- Messbarkeitssatz von Pettis
-
Das Bochner-Integral, benannt nach Salomon Bochner, ist eine Verallgemeinerung des Lebesgue-Integrals auf Banachraum-wertige Funktionen.
Inhaltsverzeichnis
Definition
Es seien
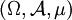 ein σ-endlicher, vollständiger Maßraum und
ein σ-endlicher, vollständiger Maßraum und 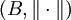 ein Banachraum.
ein Banachraum.Das Bochner-Integral
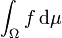 einer Funktion
einer Funktion 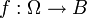 ist nun folgendermaßen definiert:
ist nun folgendermaßen definiert:Als einfache Funktion bezeichnen wir Treppenfunktionen der Gestalt
mit Faktoren
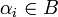 und messbaren Mengen
und messbaren Mengen 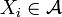 , wobei
, wobei 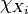 deren Indikatorfunktion bezeichnet. Das Integral einer einfachen Funktion ist nun auf naheliegende Weise definiert:
deren Indikatorfunktion bezeichnet. Das Integral einer einfachen Funktion ist nun auf naheliegende Weise definiert: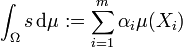 ,
,
wobei dies wohldefiniert, also unabhängig von der konkreten Zerlegung von s ist.[1]
Eine Funktion
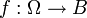 heißt μ-messbar, wenn es eine Folge
heißt μ-messbar, wenn es eine Folge 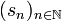 einfacher Funktionen gibt, so dass
einfacher Funktionen gibt, so dass 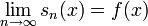 für μ-fast alle
für μ-fast alle 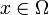 gilt.[2]
gilt.[2]Eine μ-messbare Funktion
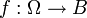 heißt Bochner-integrierbar[3], falls es eine Folge
heißt Bochner-integrierbar[3], falls es eine Folge 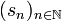 einfacher Funktionen gibt, so dass
einfacher Funktionen gibt, so dass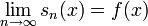 für μ-fast alle
für μ-fast alle 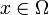 gilt und
gilt und- zu jedem
 ein
ein 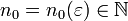 existiert mit
existiert mit
-
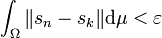 für alle
für alle 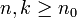 .
.
In diesem Fall ist
wohldefiniert, das heißt unabhängig von der Wahl der konkreten Folge
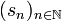 mit obigen Eigenschaften.[4] Falls
mit obigen Eigenschaften.[4] Falls 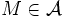 und
und 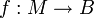 , so schreibt man
, so schreibt man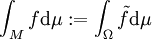 mit
mit 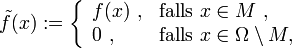
sofern
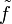 Bochner-integrierbar ist. [5]
Bochner-integrierbar ist. [5]Messbarkeitssatz von Pettis
Der folgende auf Billy James Pettis zurückgehende Satz charakterisiert die μ-Messbarkeit:
Die Funktion
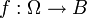 ist genau dann μ-messabar, wenn die folgenden beiden Bedingungen erfüllt sind:
ist genau dann μ-messabar, wenn die folgenden beiden Bedingungen erfüllt sind:- Für jedes stetige lineare Funktional
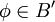 ist
ist 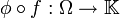 μ-messbar.
μ-messbar. - Es gibt eine μ-Nullmenge
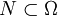 , so dass
, so dass 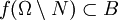 separabel bzgl. der Normtopologie ist.
separabel bzgl. der Normtopologie ist.
Ist B ein separabler Banachraum, so ist die zweite Bedingung automatisch erfüllt und damit entbehrlich. Insgesamt ist die μ-Messbarkeit B-wertiger Funktionen mit diesem Satz auf die μ-Messbarkeit skalarer Funktionen zurückgeführt.
Bochner-Integrierbarkeit
Die folgende von Bochner gefundene äquivalente Charakterisierung Bochner-integrabler Funktionen erlaubt es, einige klassische Resultate der lebesgueschen Integrationstheorie wie z.B. den Satz von der majorisierten Konvergenz auf das Bochner-Integral zu übertragen:
Eine μ-messbare Funktion
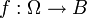 ist genau dann Bochner-integrierbar, wenn
ist genau dann Bochner-integrierbar, wenn 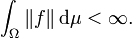
Eigenschaften
Das Bochner-Integral ist linear, das heißt, für Bochner-integrierbare Funktionen
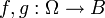 und beliebige
und beliebige 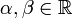 ist auch
ist auch 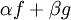 integrierbar, und es gilt:
integrierbar, und es gilt: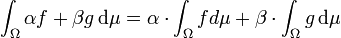 .
.
Der Satz von Radon-Nikodym gilt für das Bochner-Integral im Allgemeinen nicht. Banachräume B, für die dieser Satz gilt, bezeichnet man als Banachräume mit der Radon-Nikodym-Eigenschaft. Reflexive Räume besitzen stets die Radon-Nikodym-Eigenschaft.[6]
Literatur
- Herbert Amann, Joachim Escher: Analysis III. 1. Auflage. Birkhäuser-Verlag, Basel/Boston/Berlin 2001, ISBN 3-7643-6613-3.
- Malempati Madhusudana Rao: Measure Theory and Integration. CRC Press 2004, ISBN 0824754018, Seiten 505ff.
Weblinks
- Salomon Bochner: Integration von Funktionen, deren Werte die Elemente eines Vektorraumes sind. In: Fundamenta Mathematicae. Band 20, 1933, Seiten 262–276.
- V. I. Sobolev: Bochner integral. In: Encyclopaedia of Mathematics (englisch).
- Integrale vektorwertiger Funktionen. In: Matroids Matheplanet.
Einzelnachweise
- ↑ Herbert Amann, Joachim Escher: Analysis III. 1. Auflage. Birkhäuser-Verlag, Basel/Boston/Berlin 2001, ISBN 3-7643-6613-3, Bemerkung X.2.1 (a).
- ↑ Herbert Amann, Joachim Escher: Analysis III. 1. Auflage. Birkhäuser-Verlag, Basel/Boston/Berlin 2001, ISBN 3-7643-6613-3, Seite 65.
- ↑ Herbert Amann, Joachim Escher: Analysis III. 1. Auflage. Birkhäuser-Verlag, Basel/Boston/Berlin 2001, ISBN 3-7643-6613-3, Seite 87.
- ↑ Herbert Amann, Joachim Escher: Analysis III. 1. Auflage. Birkhäuser-Verlag, Basel/Boston/Berlin 2001, ISBN 3-7643-6613-3, Korollar X.2.7.
- ↑ Herbert Amann, Joachim Escher: Analysis III. 1. Auflage. Birkhäuser-Verlag, Basel/Boston/Berlin 2001, ISBN 3-7643-6613-3, Seite 94.
- ↑ Joseph Diestel, John Jerry Uhl: Vector Measures. Mathematical Surveys 15, American Mathematical Society, Providence, Rhode Island, ISBN 0821815156, Corollary III.2.13.
Wikimedia Foundation.