- Satz von Clarkson
-
Gleichmäßig konvexe Räume sind eine in der Mathematik betrachtete spezielle Klasse normierter Räume. Diese Räume wurden 1936 von James. A. Clarkson mittels einer geometrischen Eigenschaft der Einheitskugel eingeführt. Die gleichmäßig konvexen Banachräume sind reflexiv und haben eine für die Approximationstheorie wichtige Eigenschaft.
Inhaltsverzeichnis
Motivation und Definition
Da die Einheitskugel
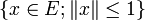 eines normierten Raums E konvex ist, liegt der Mittelpunkt
eines normierten Raums E konvex ist, liegt der Mittelpunkt 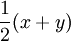 zwischen zwei Vektoren x und y der Einheitskugel wieder in der Einheitskugel. Wir untersuchen den Abstand eines solchen Mittelpunktes vom Rand der Einheitskugel.
zwischen zwei Vektoren x und y der Einheitskugel wieder in der Einheitskugel. Wir untersuchen den Abstand eines solchen Mittelpunktes vom Rand der Einheitskugel.Betrachtet man auf dem
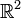 die euklidische Norm, so ist die Einheitskugel der Einheitskreis in der Ebene. Bildet man den Mittelpunkt zweier Randpunkte, so liegt dieser Mittelpunkt umso weiter im Inneren des Kreises, je weiter die beiden Randpunkte voneinander entfernt sind.
die euklidische Norm, so ist die Einheitskugel der Einheitskreis in der Ebene. Bildet man den Mittelpunkt zweier Randpunkte, so liegt dieser Mittelpunkt umso weiter im Inneren des Kreises, je weiter die beiden Randpunkte voneinander entfernt sind.Betrachtet man hingegen auf dem
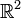 die durch
die durch 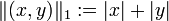 definierte Norm, so ist die 'Einheitskugel' ein Quadrat. Es gilt für e1: = (1,0),e2: = (0,1) offenbar
definierte Norm, so ist die 'Einheitskugel' ein Quadrat. Es gilt für e1: = (1,0),e2: = (0,1) offenbar 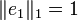 ,
, 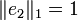 ,
, 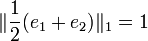 und
und 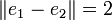 . Obwohl die beiden Randpunkte e1 und e2 sehr weit voneinander entfernt sind, liegt deren Mittelpunkt dennoch auf dem Rand der Einheitskugel.
. Obwohl die beiden Randpunkte e1 und e2 sehr weit voneinander entfernt sind, liegt deren Mittelpunkt dennoch auf dem Rand der Einheitskugel.Es ist also eine besondere geometrische Eigenschaft, dass zwei Vektoren der Einheitskugel einander nahe sein müssen, wenn deren Mittelpunkt nahe am Rand liegt. Daher definiert man:
Ein normierter Raum E heißt gleichmäßig konvex, wenn es zu jedem ε > 0 ein δ > 0 gibt, so dass folgendes gilt: Sind
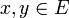 mit
mit 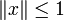 ,
, 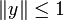 und
und 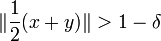 , so folgt
, so folgt 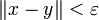 .
.Dies ist eine Eigenschaft der Norm. Geht man zu einer äquivalenten Norm über, so kann diese Eigenschaft verlorengehen, wie die beiden eingangs betrachteten Beispiele zeigen.
Beispiele
- Leicht zeigt man mittels der Parallelogrammgleichung, dass Innenprodukträume gleichmäßig konvex sind.
- J. A. Clarkson hat diese Eigenschaft für die Banachräume Lp[0,1] ,
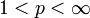 , nachgewiesen (Satz von Clarkson). Diese Aussage ist 1950 von E. J. McShane wesentlich verallgemeinert worden. Ist E ein gleichmäßig konvexer Raum, μ ein beliebiges positives Maß,
, nachgewiesen (Satz von Clarkson). Diese Aussage ist 1950 von E. J. McShane wesentlich verallgemeinert worden. Ist E ein gleichmäßig konvexer Raum, μ ein beliebiges positives Maß, 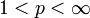 , so ist auch Lp(μ,E) gleichmäßig konvex. Dabei ist Lp(μ,E) der Banachraum der Äquivalenzklassen messbarer Funktionen f mit Werten in E, so dass
, so ist auch Lp(μ,E) gleichmäßig konvex. Dabei ist Lp(μ,E) der Banachraum der Äquivalenzklassen messbarer Funktionen f mit Werten in E, so dass 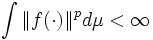 .
.
- 1967 hat C. A. McCarthy die gleichmäßige Konvexität für die Schatten-Klassen mit
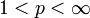 nachgewiesen.
nachgewiesen.
Satz von Milman
David Milman hat eine weitere wichtige Eigenschaft gleichmäßig konvexer Räume bewiesen:
Satz von Milman: Gleichmäßig konvexe Banachräume sind reflexiv.
Dieses Resultat ist unabhängig von Milman auch von Billy James Pettis (1913–1979) gefunden worden, weshalb man manchmal auch vom Satz von Milman-Pettis spricht. Die Klasse der gleichmäßig konvexen Räume ist echt kleiner als die Klasse der reflexiven Räume, denn es gibt reflexive Banachräume, die nicht isomorph zu gleichmäßig konvexen Räumen sind.
Man kann sogar zeigen, dass gleichmäßig konvexe Banachräume die Banach-Saks-Eigenschaft haben (ein Satz von S. Kakutani), und dass Banachräume mit Banach-Saks-Eigenschaft reflexiv sind (ein Satz von T. Nishiura and D. Waterman).
Strikte Konvexität
Ein normierter Raum E heißt strikt konvex (oder auch strikt normiert), wenn aus
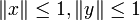 und
und 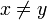 stets
stets 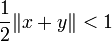 folgt. Man kann leicht zeigen, dass gleichmäßig konvexe Räume strikt konvex sind. Man hat daher folgende Inklusionen von Klassen normierter Räume:
folgt. Man kann leicht zeigen, dass gleichmäßig konvexe Räume strikt konvex sind. Man hat daher folgende Inklusionen von Klassen normierter Räume:Innenprodukträume 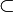 Gleichmäßig konvexe Räume
Gleichmäßig konvexe Räume 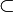 Strikt konvexe Räume
Strikt konvexe Räume 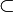 Normierte Räume.
Normierte Räume.Der Approximationssatz
Die folgenden Aussagen, die auch als Approximationssatz bezeichnet werden, zeigen die Bedeutung der gleichmäßig konvexen Räume für die Approximationstheorie. Viele Approximationsprobleme lassen sich so umformulieren, dass in einer konvexen Menge (z.B. in einem Unterraum) ein Vektor zu finden ist, der zu einem gegebenen Vektor kürzesten Abstand hat. Es gelten folgende Aussagen für einen reellen normierten Raum E,
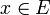 und eine abgeschlossene und konvexe Teilmenge
und eine abgeschlossene und konvexe Teilmenge 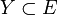 :
:- Eindeutigkeit: Ist E strikt konvex, so gibt es höchstens ein
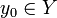 mit
mit 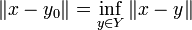 .
. - Existenz: Ist E ein gleichmäßig konvexer Banachraum, so gibt es ein (nach obigem eindeutig bestimmtes)
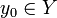 mit
mit 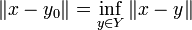 .
.
Konvexitätsmodul
Man setzt für eine Zahl
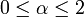
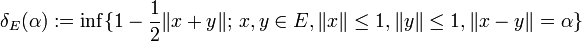
und nennt die dadurch definierte Funktion
![\delta_E:[0,2]\rightarrow [0,1]](/pictures/dewiki/50/2830c239a61ea998897d7e9c2df6a786.png) den Konvexitätsmodul von E. Für gleichmäßig konvexe Räume gilt definitionsgemäß δE(α) > 0 für alle α > 0, und man kann zeigen, dass der Konvexitätsmodul eine monotone Funktion ist, sogar die Abbildung
den Konvexitätsmodul von E. Für gleichmäßig konvexe Räume gilt definitionsgemäß δE(α) > 0 für alle α > 0, und man kann zeigen, dass der Konvexitätsmodul eine monotone Funktion ist, sogar die Abbildung 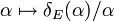 ist monoton. Ein Satz von M. Kadets stellt eine notwendige Bedingung für die unbedingte Konvergenz von Reihen in gleichmäßig konvexen Räumen dar:
ist monoton. Ein Satz von M. Kadets stellt eine notwendige Bedingung für die unbedingte Konvergenz von Reihen in gleichmäßig konvexen Räumen dar:Ist (xn)n eine Folge in einem gleichmäßig konvexen Raum E mit
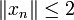 für alle
für alle 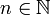 und ist die Reihe
und ist die Reihe 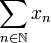 unbedingt konvergent, so gilt
unbedingt konvergent, so gilt 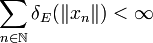
Literatur
- James A. Clarkson: Uniformly convex spaces. Transactions of the American Mathematical Society, Band 40, 1936, Seite 396–414.
- Mahlon M. Day: Reflexive Banach spaces not isomorphic to uniformly convex spaces. Bulletin of the American Mathematical Society, Band 47, Nr. 4, 1941, Seiten 313-317.
- D. Milman: On some criteria for the regularity of spaces of type (B). Comptes Rendus (Doklady) de l'Académie des Sciences de l'URSS, Band 20, 1938, Seiten 243–246.
- B. J. Pettis: A proof that every uniformly convex space is reflexive. Duke Math. J., Band 5, 1939, Seiten 249–253.
- Friedrich Hirzebruch, Winfried Scharlau: Einführung in die Funktionalanalysis. 1971, ISBN 3-860-25429-4.
- Joseph Diestel: Sequences and Series in Banach Spaces. 1984, ISBN 0-387-90859-5.
Wikimedia Foundation.
