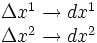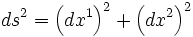Metrischer Tensor der Ebene
Schlagen Sie auch in anderen Wörterbüchern nach:
Auflösbar — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Euklidisch — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Fehlstand — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Integrabel — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Kollinear — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Kopunktal — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Mathematisches Attribut — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Multivariat — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Primitives Element — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
Semilinear — In diesem Glossar werden kurze Erklärungen mathematischer Attribute gesammelt. Unter einem Attribut wird eine Eigenschaft verstanden, die einem mathematischen Objekt zugesprochen wird. Ein Attribut hat oft die Form eines Adjektivs (endlich, offen … Deutsch Wikipedia
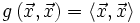
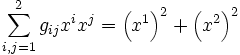
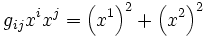
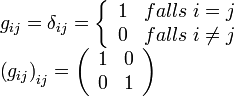
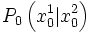 und
und 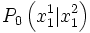 . Der Abstand zwischen diesen beiden Punkten ist dann definiert als die Länge des verbindenden Vektors
. Der Abstand zwischen diesen beiden Punkten ist dann definiert als die Länge des verbindenden Vektors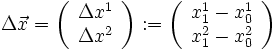
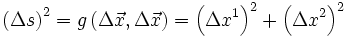
 gehen, wird sozusagen
gehen, wird sozusagen