Ebene (Mathematik)

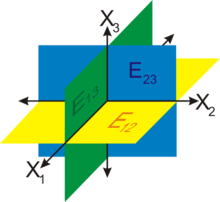Die 3 Koordinatenebenen

Die Ebene ist ein Grundbegriff der Geometrie. Allgemein handelt es sich um ein unbegrenzt ausgedehntes flaches zweidimensionales Objekt.

• Hierbei bedeutet unbegrenzt ausgedehnt und flach, dass zu je zwei Punkten auch eine durch diese verlaufende Gerade vollständig in der Ebene liegt.
• Zweidimensional bedeutet, dass – abgesehen von enthaltenen Geraden – kein echter Teilraum ebenfalls diese Eigenschaft hat.

Konkreter bezeichnet man mit Ebene, je nach Teilgebiet der Mathematik, allerdings durchaus verschiedene Objekte.

Ebene als eigenständiges Objekt

kleinste projektive Ebene (sieben Punkte, sieben Geraden)

kleinste affine Ebene (vier Punkte, sechs Geraden)

Der klassische Ebenenbegriff nach Euklid

In der klassischen Geometrie etwa im Sinne von Euklids Elementen bildet die (euklidische) Ebene – in diesem Zusammenhang üblicherweise mit dem bestimmten Artikel bezeichnet – den Rahmen geometrischer Untersuchungen, etwa für Konstruktionen mit Zirkel und Lineal. Man kann sie sich vorstellen als Abstraktion der Zeichenebene (Papier) als unendlich ausgedehnt und unendlich flach, so wie die Gerade eine als unendlich dünn und unendlich lang vorgestellte Abstraktion des gezeichneten Strichs (Bleistiftlinie) ist. Die euklidische Geometrie wird heutzutage durch Hilberts Axiomensystem der euklidischen Geometrie beschrieben.

Seit Descartes die euklidische Ebene mit Koordinaten versehen hat, kann man die euklidische Ebene identifizieren mit der Menge $\mathbb R^2$ aller Paare reeller Zahlen. Oder andersherum: $\mathbb R^2$ bildet ein Modell für die Hilbertschen Axiome der Ebene. Dieser reelle Vektorraum wird daher ebenfalls als Ebene bezeichnet.

Die Projektive Ebene

Ergänzt man Euklids affine Ebene um eine unendlich ferne Gerade und auf ihr liegende unendlich ferne Punkte, erhält man eine projektive Ebene.

Auch die projektive Ebene lässt sich algebraisch beschreiben, nämlich als die Menge aller eindimensionalen Unterräume im $\mathbb R^3$. Man fasst also die durch den Ursprung verlaufenden Geraden als Punkte der projektiven Ebene auf. Die Geraden der projektiven Ebene sind dann genau die zweidimensionalen Untervektorräume von $\mathbb R^3$, also die durch den Ursprung verlaufenden „herkömmlichen“ Ebenen.

Verallgemeinerungen

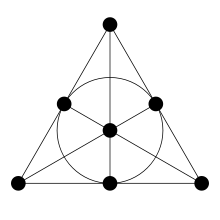
Schwächt man das Hilbertsche Axiomensystem ab, so sind sogar endliche Strukturen möglich, die auch als affine oder projektive Ebene bezeichnet werden. Die Abbildung rechts zeigt eine endliche projektive Ebene mit sieben Punkten und sieben Geraden. Durch Entfernen einer beliebigen Gerade und der auf ihr liegenden Punkte erhält man eine endliche affine Ebene mit vier Punkten und sechs Geraden.

In Verallgemeinerung des kartesischen Modells der euklidischen Ebene wird auch für beliebige Körper K der zweidimensionale Vektorraum K² als affine Ebene bezeichnet; entsprechend für die projektive Ebene. Man beachte: Ist K der Körper $\mathbb C$ der komplexen Zahlen, die ja durch die Gaußsche Zahlenebene veranschaulicht werden, so ist bereits $\mathbb C$ (reell) zweidimensional, wird aber als komplexe Gerade bezeichnet. Die Ebene $\mathbb C^2$ ist reell vierdimensional, aber nur ein zweidimensionaler komplexer Vektorraum. Der Körper K kann auch ein endlicher Körper sein. Im Fall $K=\mathbb F_2$ erhält man die oben beschriebene kleinste endliche affine Ebene mit vier Punkten bzw. die projektive Ebene mit sieben Punkten.

Eine Fläche im Sinne der Topologie ist die Ebene (auch die projektive) nur im Fall $K=\R$; im Falle $K=\mathbb C$ handelt es sich immerhin noch um eine differenzierbare Mannigfaltigkeit.

Ebene als Teilraum

Zwei sich schneidende Ebenen

Betrachtet man höherdimensionale geometrische Räume, so bezeichnet man jeden Teilraum, der isomorph zu einer Ebene im obigen Sinne ist, als eine Ebene. In einem dreidimensionalen Euklidischen Raum ist eine Ebene dabei festgelegt durch

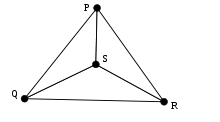
• drei nicht kollineare Punkte
• eine Gerade und einen nicht auf ihr liegenden Punkt
• zwei sich schneidende Geraden oder
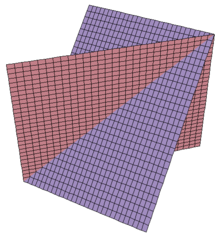
• zwei echt parallele Geraden

Liegen zwei Geraden windschief zueinander, so liegen sie dagegen nicht in einer gemeinsamen Ebene. Stattdessen gibt es dann zwei parallele Ebenen, deren jede je eine der Geraden enthält.

Zwei Ebenen sind entweder parallel, schneiden sich in einer Geraden oder sind identisch. Sie können im (dreidimensionalen) Raum also nicht windschief zueinander liegen. Im ersten Fall ist jede zur ersten Ebene senkrechte Gerade auch senkrecht zur zweiten. Die Länge der Strecke, die die Ebenen auf solch einer Geraden begrenzen, bezeichnet man als den Abstand der Ebenen. Im zweiten Fall betrachtet man eine zur Schnittgeraden senkrechte Ebene. Mit dieser schneiden sich die beiden ersten Ebenen in zwei Geraden. Den Winkel zwischen diesen Geraden bezeichnet man als Winkel zwischen den beiden Ebenen.

Jeder zweidimensionale Untervektorraum von $\mathbb R^n$ (bzw. Kⁿ) bildet eine Ebene. Affine zweidimensionalen Unterräume sind parallel verschobene Ebenen, die den Nullpunkt des Raums nicht enthalten.

Nicht jedes unter den Begriff der Ebene fallende mathematische Objekt lässt sich als Teilraum eines entsprechenden höherdimensionalen Raumes auffassen. So ist etwa die Moulton-Ebene eine affine Ebene, in der der Satz von Desargues nicht gilt, während er in jedem dreidimensionalen affinen Raum – und damit in jeder enthaltenen Ebene – immer gilt.

Ebenengleichung

Im Falle einer Teilebene höherdimensionale Räume, insb. des $\Bbb R^n$, lässt sich diese Ebene auf verschiedene Weise beschreiben durch geeignete Gleichungen für den Ortsvektor $\vec r$ bzw. für die Koordinaten x,y,z (ggf. weitere).

Gleichungen im dreidimensionalen Raum

Bekannt ist vor allem die Normalenform (oder implizite Form), die sich eines Normalenvektors $\vec n$ der Ebene bedient. Weiter wird eine Zahl λ angegeben, um die Position der Ebene zu bestimmen, da der Normalvektor nur die Schräglage der Ebene festlegt; er definiert eine Schar von parallelen Ebenen. λ ergibt sich dabei aus $\vec n \cdot \vec p$, wobei $\vec p$ einen beliebigen Punkt in der Ebene repräsentiert. Die Vektoren $\vec q$ vom Ursprung zu einem Punkt auf der Ebene (Ortsvektoren) erfüllen dann die Gleichung

$\vec n \cdot \vec q = \lambda$.

Beispiel:

$\vec n = \begin{pmatrix}1 \\-2 \\3 \end{pmatrix} , \; \vec p = \begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix}, \; \vec q = \begin{pmatrix}x\\y\\z\end{pmatrix} , \; \lambda = \vec n \cdot \vec p = 5$

$\Rightarrow \begin{align}\vec n\cdot\vec q&=\lambda\\x-2y+3z&=5\\\end{align}$

Eine andere gängige Variante ist die Parameterdarstellung, bei der ein Punkt P auf der Ebene gegeben ist und zwei in der Ebene verlaufende linear unabhängige Vektoren $\vec v_1, \vec v_2$ (Richtungsvektoren oder Spannvektoren).

Die Ebene wird definiert durch die Gleichung

$\vec q = \vec p + s \cdot \vec v_1 + t \cdot \vec v_2$,

wobei $\vec p=\overrightarrow{OP}$.

Jedes Wertepaar $s,t \in \mathbb{R}$ liefert den Ortsvektor $\vec q$ eines Punktes der Ebene. Dieser Vektor erfüllt die oben angeführte Normalgleichung.

Die obige Beispielebene sieht in Parameterdarstellung so aus:

$\vec p = \begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix}, \; \vec v_1 = \begin{pmatrix} 5 \\ 1 \\ -1 \end{pmatrix} , \; \vec v_2 = \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}$

$\vec q = \begin{pmatrix} 5 \\ 0 \\ 0 \end{pmatrix} + s \cdot \begin{pmatrix} 5 \\ 1 \\ -1 \end{pmatrix} + t \cdot \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}$

Um von der Parameterdarstellung zur Normalenform zu gelangen, bildet man das Kreuzprodukt der beiden Richtungsvektoren und erhält so einen Normalenvektor:

$\vec v_1 \times \vec v_2 = \vec n$.

Verallgemeinerungen auf höhere Dimensionen

In höherdimensionalen Räumen $\Bbb R^n$ funktioniert die Parameterdarstellung weiterhin. Es gibt aber kein Kreuzprodukt mehr, mit dem man hieraus einen (bis auf die Länge) eindeutig bestimmten Normalvektor erhält. Stattdessen muss man ein der Normalform analoges Verfahren anders beschreiben. Man benötigt insgesamt n − 2 linear unabhängige Normalvektoren zu der Ebene und hat dann für jeden hiervon eine Gleichung der Form $\vec n_i \cdot \vec r = b_i$, $i=1,\ldots,n-2$, welche alle simultan zu erfüllen sind. Dies kann man zusammenfassen zu

$A\cdot \vec r = \vec b,$

wobei A eine $(n-2)\times n$-Matrix und $\vec b$ ein Vektor mit n − 2 Komponenten ist. Die Zeilen von A entsprechen den $\vec n_i$, die Komponenten von $\vec b$ den b_i. Die Bedingung, dass die $\vec n_i$ linear unabhängig sein müssen, entspricht der Bedingung, dass A den Rang n − 2 haben muss.

Siehe auch

• Affine Ebene
• Hessesche Normalform
• Planarität, das Maß für die Ebenheit
• Spurgerade
• Formelsammlung Analytische Geometrie

Weblinks

• lernzentrum.de Erklärungen zu Geraden, Ebenen, ihrer gegenseitigen Lage, Abständen und Winkeln mit frei drehbaren dreidimensionalen Applets
• Mathewiki: Ebene Darstellungsformen von Ebenen mit Beispielen