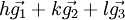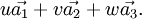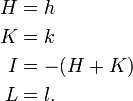Miller-Indizes

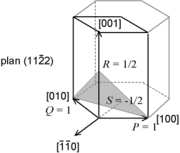
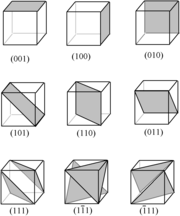Auswahl millerscher Indizes in einem Würfel (Koordinatenurspung an der Ecke vorn links unten; x- nach rechts, z- nach oben, y-Achse in die Bildebene)

Millersche Indizes dienen in der Kristallographie der eindeutigen Bezeichnung von Ebenen und Richtungen (bzw. Vektoren) in Kristallsystemen, somit der Kristallorientierung. Die Schreibweise wurde im Jahr 1839 von William Hallowes Miller (1801–1880) vorgeschlagen.

Beispiele für ihren Einsatz sind:

• in der Kristallmorphologie werden sie verwendet, um die Kristallflächen eindeutig zu beschreiben.
• bei Beugungsmethoden, wie der Röntgenbeugung oder der Elektronenbeugung, bezeichnen sie eine Netzebenen-Schar. Hier werden auch höhere Indizes – beispielsweise (222) – eingesetzt, um die Beugung höherer Ordnung anzugeben. Daher wird zur Abgrenzung auch der Begriff Bragg-Indizes benutzt (s. a. Bragg-Gleichung).
• in der Materialwissenschaft werden sowohl Gitterebenen als auch Gittervektoren benötigt, um verschiedene Gitterfehler zu charakterisieren.

Notation

Gitterebene

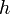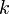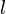Drei ganzzahlige Indizes $h\!\,$, $k\!\,$ und $l\!\,$ bilden das Zahlentriplett 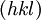$(hkl)\!\,$, dies sind die millerschen Indizes. Negative Indizes werden mit einem über die Zahl geschriebenen Balken gekennzeichnet, also beispielsweise 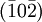$(\bar 1 0 \bar 2)\!\,$. Dieses Triplett bezeichnet eine spezifische Ebene.

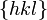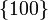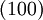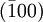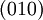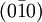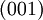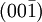Sind anstatt einer spezifischen Netzebene auch kristallographisch äquivalente Ebenen gemeint, so wird die Notation $\{hkl\}\!\,$ verwendet. Beispielsweise bezeichnet man mit $\{1 0 0\}\!\,$ in einem kubischen Gitter die aufgrund der kubischen Symmetrie äquivalenten Ebenen $(1 0 0)\!\,$, $(\bar 1 0 0)\!\,$, $(0 1 0)\!\,$, $(0 \bar 1 0)\!\,$, $(0 0 1)\!\,$ und $(0 0 \bar 1)\!\,$, was den sechs Oberflächen eines Würfels entspricht.

Da eine Netzebenen-Schar auch immer einen Punkt im Reziproken Gitter des Kristalls darstellt, kann mit dem Triplett 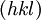$(hkl)\!\,$ auch ein Vektor im reziproken Raum bezeichnet werden.

Gittervektoren

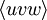Auch Vektoren innerhalb des Gitters können durch die millerschen Indizes bezeichnet werden. Dabei wird die Notation $[u v w]\!\,$ verwendet, um einen spezifischen Vektor zu bezeichnen. Die Notation $\langle u v w \rangle\!\,$ bezeichnet alle zum Vektor $[u v w]\!\,$ kristallographisch äquivalenten Richtungen.

Definition

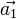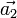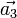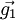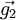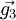Abhängig von seinem Kristallsystem wird jedem Kristall ein Koordinatensystem zugeordnet. Die drei Vektoren $\vec{a_1}$, $\vec{a_2}$ und $\vec{a_3}$ mögen die Basis dieses Gitterkoordinatensystems bilden. Die Basis des zugehörigen Reziproken Gitters sei durch die Vektoren $\vec{g_1}$, $\vec{g_2}$ und $\vec{g_3}$ gegeben.

Gitterebene

Es ergeben sich zwei äquivalente Möglichkeiten eine Gitterebene zu definieren.

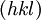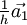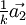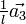Zum Einen bezeichnet der Index $( h k l )\!\,$ die Ebene, die durch die drei Punkte $\tfrac{1}{h} \vec{a_1}$, $\tfrac{1}{k} \vec{a_2}$ und $\tfrac{1}{l} \vec{a_3}$ geht. Also schneiden die Basisvektoren des jeweiligen Kristallsystems die Ebenen gerade an den Kehrwerten der einzelnen Indizes. Ein Index von Null bezeichnet dabei einen Schnittpunkt im Unendlichen, d.h. der zugehörige Basisvektor ist parallel zur Ebene.

Die andere Möglichkeit ist, mit 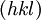$( h k l )\!\,$ den reziproken Gittervektor

$h \vec{g_1} + k \vec{g_2} + l \vec{g_3}$

zu bezeichnen. Dieser Vektor steht senkrecht auf den entsprechenden Gitterebenen.

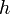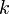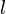Dabei werden diejenigen ganzen Zahlen $h\!\,$, $k\!\,$ und $l\!\,$ verwendet, die keinen gemeinsamen Teiler mehr haben. Dies entspricht dem kürzesten reziproken Gittervektor, der senkrecht auf der Ebene steht.

Gittervektor

Entsprechend beschreibt die Notation $[ u v w ]\!\,$ einen Vektor im realen Gitter

$u \vec{a_1} + v \vec{a_2} + w \vec{a_3}.$

Dieser Vektor steht im Allgemeinen nicht senkrecht auf der Ebene 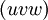$( u v w )\!\,$. Dies ist nur im kubischen Gitter der Fall.

Vierer-Schreibweise

Millersche Indizes im hexagonalen Kristallsystem

Im trigonalen Kristallsystem und im hexagonalen Kristallsystem wird häufig die Schreibweise 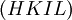$(HKIL)\!\,$ bevorzugt. Die Ebenen-Indizes der Vierer-Schreibweise ergeben sich aus der herkömmlichen Dreier-Schreibweise 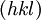$(hkl)\!\,$ als:

$\begin{align} H & = h\\ K & = k\\ I & = -(H+K)\\ L & = l.\\ \end{align}$

Auch für die Richtungs-Indizes, gibt es eine Vierer-Schreibweise: $[UVTW]\!\,$. Die Umrechnung aus der Dreier-Schreibweise $[uvw]\!\,$ ist unterschiedlich zur Umrechnung der Ebenen-Indizes:

$\begin{align} U & = \tfrac{1}{3}(2u - v)\\ V & = \tfrac{1}{3}(2v - u)\\ T & = -(U+V)\\ W & = w.\\ \end{align}$

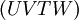Der Vorteil der Vierer-Schreibweise liegt darin, dass der Vektor $[UVTW]\!\,$, ähnlich wie in kubischen Kristallsystemen, senkrecht auf der Ebene $(UVTW)\!\,$ steht. In der Dreier-Schreibweise ist dies in diesen Kristallsystemen im Allgemeinen nicht der Fall.

Literatur

• Werner Schatt, H. Worch: Werkstoffwissenschaft. 8. Aufl., Dt. Verl. für Grundstoffindustrie, Stuttgart 1996. ISBN 3-342-00675-7
• Charles Kittel: Introduction to solid state physics. 7. Aufl., New York, Wiley 1996. ISBN 0-471-11181-3

Weblinks

• Richtungen und Ebenen im Gitter bei der Universität Kiel
• Videovorlesung der Universität Tübingen