Modellprüfverfahren

Model Checking (deutsch auch Modellprüfung) ist ein Verfahren zur vollautomatischen Verifikation einer Systembeschreibung (Modell) gegen eine Spezifikation (Formel). Der Begriff ist motiviert durch die mathematische Formulierung des Problems: Für eine gegebene Systembeschreibung M und eine gegebene logische Eigenschaft φ, prüfe, ob M Modell ist für φ (formal $M \models \varphi$).

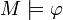Das Verfahren wird als vollautomatisch bezeichnet, weil es keiner Benutzerinteraktion bedarf (im Gegensatz zu einigen deduktiven Verfahren, wie zum Beispiel interaktives Theorembeweisen). Die Systembeschreibung erfolgt in einer formalen Sprache, zum Beispiel durch ein Programm, einen endlichen Automaten, oder durch ein Transitionssystem. Der Zustandsraum des Systems muss nicht notwendigerweise endlich, jedoch endlich repräsentierbar sein. Die Spezifikation ist die nachzuweisende formale Eigenschaft des Systems, gegeben zum Beispiel durch eine temporal-logische Formel oder durch einen Beobachtungsautomaten.

Prinzip

Eingabe des Modellprüfers (engl. model checkers) sind die Systembeschreibung und die Spezifikation. Erfüllt die Systembeschreibung die Spezifikation, stoppt der Algorithmus und liefert ein Korrektheitszertifikat als Ausgabe. Findet der Algorithmus eine Verletzung der Spezifikation, stoppt der Algorithmus und liefert als Ausgabe ein Gegenbeispiel. Dies ist meist eine mögliche Systemausführung, die das Verletzen der Spezifikation nachweist.

Temporal-logische Logiken

Bei der logischen Formel, der formalisierten Spezifikation, handelt es sich oft um eine Formel einer temporalen Logik. Diese macht eine Aussage über das zu prüfende Verhalten des Systems über die Zeit (z.B. In keiner Ausführung kommt es zu einem Deadlock). Solche Eigenschaften lassen sich in einer der folgenden häufig verwendeten Logiken ausdrücken.

• Modaler Mu-Kalkül
• Computation Tree Logic (kurz CTL)
• Linear Time Temporal Logic (kurz LTL)
• CTL*

Beim modalen μ-Kalkül handelt es sich um ein auf Fixpunktoperatoren über den Zuständen des Modelles beruhenden Ansatz (in der Liste der genannten Logiken stellt er die mächtigste Logik dar und umfasst die anderen). In der praktischen Anwendung sind die Logiken CTL*, CTL und LTL jedoch weitaus häufiger vertreten.

CTL* stellt eine Obermenge der beiden Logiken CTL und LTL dar. Ferner lassen sich Aussagen aus CTL und LTL i.A. nicht ineinander überführen.

Typen von Algorithmen des Model Checkings

Die Algorithmen des Model Checkings werden in zwei Typen unterschieden.

Explizites Model Checking

Explizites Model Checking baut das Transitionssystem in geeigneter Weise auf und exploriert es bzgl. der zu prüfenden Eigenschaft.

Automaten-basiertes LTL-Model Checking

Ein bekannter Ansatz zum Verifizieren von LTL-Formeln benutzt Büchi-Automaten. Hierbei werden zunächst sowohl das zu prüfende System, wie auch die Eigenschaft selbst in einen Büchi-Automaten überführt. Diese Automaten seien mit B(M) bzw. B(φ) bezeichnet.

Nun erfüllt das System M die Eigenschaft φ genau dann, wenn B(M) eine Teilmenge der zulässigen durch den Eigenschaftsautomaten B(φ) beschriebenen Systemevolutionen realisieren kann; wenn also für die durch die Büchi-Automaten beschriebenen Sprachen folgende Inklusionsbeziehung gilt:

$Lang(B(M)) \subseteq Lang(B(\phi))$.

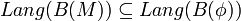Dies lässt sich umformen zu

$Lang(B(M)) \cap \overline{Lang(B(\phi))} = \emptyset$.

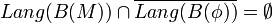Dies ist wiederum äquivalent zu

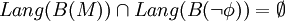$Lang(B(M)) \cap Lang(B(\neg\phi)) = \emptyset$ bzw. $Lang(B(M) \cap B(\neg\phi)) = \emptyset$.

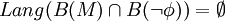Es reicht also, für die negierte Eigenschaft, einen Büchi-Automat zu konstruieren und diesem mit dem für das System konstruierten Büchi-Automaten zu verschneiden. Beschreibt das Ergebnis die leere Sprache, so ist die Eigenschaft erfüllt. Ansonsten beschreibt der resultierende Automat genau die Systemevolutionen, die zum Scheitern der Eigenschaft führten.

CTL-Model Checking

Bei CTL-Formeln werden an den Zuständen schrittweise Teilformeln auf ihre Wahrheitswerte überprüft.

Der Zustandsraumexplosion kann z.B. durch Ausnutzen von Symmetrien und Partial Order Reduction entgegengewirkt werden, um möglichst große Transitionssysteme verifizieren zu können.

Symbolisches Model Checking

Symbolische Modellprüfer basieren entweder auf Binären Entscheidungsdiagrammen (z. B. für CTL-Formeln) oder auf SAT-Solvern (z.B. für LTL-Formeln). Im ersten Fall wird je ein BDD (engl. binary decision diagram, Binäres Entscheidungsdiagramm) für die Zustandsübergangsrelation und die erfüllbaren Zustände der Formel aufgebaut. Im zweiten Fall werden Modell und Spezifikation in eine aussagenlogische Formel umgewandelt, die anschließend auf Erfüllbarkeit überprüft wird.

Praktischer Einsatz

Seit Anfang der 90er Jahre wurden große Fortschritte in der Performance der Algorithmen erzielt, wodurch das Verfahren für die Praxis interessant geworden ist. In der Qualitätssicherung beim Entwurf großer integrierter Schaltungen werden Modellprüfer bereits in der industriellen Praxis eingesetzt. In den letzten Jahren wurden in einigen Forschungsprojekten Modellprüfer für Software entwickelt.

Literatur

• Baier, Katoen: "Principles of Model Checking", MIT Press, 2008. ISBN 978-0-262-02649-9

Grundlegende Einfuehrung mit sehr vielen Beispielen.

• Clarke, Grumberg, Peled: Model Checking. MIT Press, 2000. ISBN 0-262-03270-8

(Gilt als erste größere zusammenfassende Veröffentlichung, bisher Standardwerk auf dem Gebiet.)

• Peled: Software Reliability Methods. Springer-Verlag, 2001. ISBN 0-387-95106-7
• B. Berard, M. Bidoit, A. Finkel, F. Laroussinie, A. Petit, L. Petrucci, P. Schnoebelen: Systems and Software Verification: Model-Checking Techniques and Tools, ISBN 3-540-41523-8

(Neben einem Teil mit theoretischen Grundlagen und anschaulichen Beispielen, stellt das Buch in einem zweiten Teil diverse unterschiedliche Werkzeuge und deren typische Anwendungsgebiete vor.)

• Julian Bradfield, Colin Stirling: Modal logics and mu-calculi
• Markus Müller-Olm, David A. Schmidt, Bernhard Steffen: Model checking: a tutorial introduction. Proc. 6th Static Analysis Symposium, G. File and A. Cortesi, eds., Springer LNCS 1694, 1999, pp. 330-354.

(In einer kurzen Übersicht werden unterschiedliche Modellierungtypen sowie Logiken und im speziellen der modale Mu-Kalkül vorgestellt.)