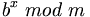Modulare Exponenziation

Die diskrete Exponentialfunktion (Synonyme Bezeichnungen sind modulare Exponentiation oder modulares Potenzieren)

$b^x\ mod\ m$

liefert den Rest bei Division von b^x durch m. Die Umkehrung der diskreten Exponentialfunktion heißt diskreter Logarithmus.

Die diskrete Exponentialfunktion ist auch für große Exponenten effizient berechenbar. Für die Umkehrung, also die Berechnung des Exponenten x, bei gegebener Basis b, Modul m und gewünschtem Ergebnis, ist allerdings bis heute kein schneller Algorithmus bekannt. Die diskrete Exponentialfunktion wird daher als Einwegfunktion in asymmetrischen Kryptosystemen verwendet.

Zur Berechnung der diskreten Exponentialfunktion kann man folgenden Algorithmus verwenden:

function expmod(b,x,m : integer) : integer;
   /* 
    Berechnet die diskrete Exponentialfunktion b hoch x modulo m
    unter ausschließlicher Verwendung der Operationen Quadrieren
    und Multiplizieren. Der Rest wird nach jeder Operation bestimmt, 
    um große Zwischenergebnisse zu vermeiden 
    mod bezeichnet die Modulo-Operation
    div bezeichnet die ganzzahlige Division
   */
   Quad := b
   Halb := x
   Erg := 1
   while Halb > 0
      if Halb mod 2 > 0 then 
         Erg := (Erg * Quad) mod m
      endif
      Quad = (Quad * Quad) mod m 
      Halb = Halb div 2
   end while
   return Erg
end;

Der Algorithmus in C:

int mod_exp(int b, int x, int m)
{
	int erg = 1;
	while ( x > 0 ) 
	{
		if ( x & 1 ) { erg = ( erg * b ) % m; }
		b = ( b * b ) % m;
		x = x >> 1;
	}
	return erg;
}

Das Verfahren benötigt höchstens 2 * log₂(x) Multiplikationen modulo m. Es beruht auf der gleichen Idee (fortgesetztes Quadrieren und Multiplizieren), wie das unter Russische Bauernmultiplikation beschriebene Verfahren zur schnellen Potenzierung.

Weblinks

• Applet für Fast Modular Exponentiation