- Montelraum
-
Der mathematische Begriff Montel-Raum bezeichnet eine spezielle Klasse lokalkonvexer Räume. Ihren Namen tragen sie nach dem Satz von Montel aus der Funktionentheorie. Viele lokalkonvexe Räume aus der Theorie der Distributionen sind Montelräume.
Inhaltsverzeichnis
Definition
Ein lokalkonvexer Raum heißt Montel-Raum, wenn er quasitonneliert ist und der Abschluss jeder beschränkten Menge kompakt ist.
Beispiele
- Ein normierter Raum ist genau dann Montelraum, wenn er endlich-dimensional ist.
- Ist
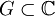 ein Gebiet und ist H(G) der Raum der holomorphen Funktionen auf G mit den Halbnormen
ein Gebiet und ist H(G) der Raum der holomorphen Funktionen auf G mit den Halbnormen 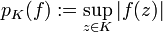 , wobei
, wobei 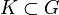 die kompakten Teilmengen von G durchläuft, so hat nach dem Satz von Montel jede in H(G) beschränkte Menge einen kompakten Abschluss. Da H(G) als Fréchetraum auch quasitonneliert ist, erweist sich H(G) als Montel-Raum.
die kompakten Teilmengen von G durchläuft, so hat nach dem Satz von Montel jede in H(G) beschränkte Menge einen kompakten Abschluss. Da H(G) als Fréchetraum auch quasitonneliert ist, erweist sich H(G) als Montel-Raum. - Sei
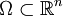 offen und
offen und 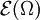 der Raum der beliebig oft differenzierbaren Funktionen
der Raum der beliebig oft differenzierbaren Funktionen 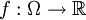 mit den Halbnormen
mit den Halbnormen 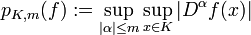 , so ist
, so ist 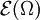 ein Montel-Raum. Dabei wurde für
ein Montel-Raum. Dabei wurde für 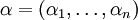 die Multiindex-Schreibweise verwendet.
die Multiindex-Schreibweise verwendet. - Sei
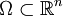 offen und
offen und 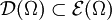 der Unterraum der beliebig oft differenzierbaren Funktionen mit einem kompakten Träger in Ω. Für kompaktes
der Unterraum der beliebig oft differenzierbaren Funktionen mit einem kompakten Träger in Ω. Für kompaktes 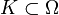 sei
sei 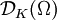 der Raum der Funktionen mit Träger in K mit der von
der Raum der Funktionen mit Träger in K mit der von 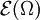 induzierten Teilraumtopologie. Dann gibt es eine feinste lokalkonvexe Topologie auf
induzierten Teilraumtopologie. Dann gibt es eine feinste lokalkonvexe Topologie auf 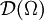 , die alle Einbettungen
, die alle Einbettungen 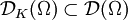 stetig macht.
stetig macht. 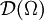 mit dieser Topologie ist der Raum der Testfunktionen und ist ein Beispiel für einen nicht-metrisierbaren Montel-Raum.
mit dieser Topologie ist der Raum der Testfunktionen und ist ein Beispiel für einen nicht-metrisierbaren Montel-Raum. - Sei
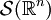 der Raum aller Funktionen
der Raum aller Funktionen 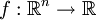 , für die alle Suprema
, für die alle Suprema 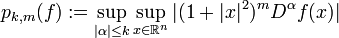 endlich sind. Dabei wurde wieder von der Multiindex-Schreibweise Gebrauch gemacht. Der Raum
endlich sind. Dabei wurde wieder von der Multiindex-Schreibweise Gebrauch gemacht. Der Raum 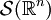 mit den Halbnormen
mit den Halbnormen 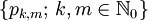 heißt Raum der schnell fallenden Funktionen und ist ein Montel-Raum.
heißt Raum der schnell fallenden Funktionen und ist ein Montel-Raum. - Vollständige quasitonnelierte Schwartz-Räume sind Montel-Räume.
- Jeder lokalkonvexe Raum mit der feinsten lokalkonvexen Topologie, d.h. mit der von allen absolutkonvexen, absorbierenden Mengen als Nullumgebungsbasis erzeugten Topologie, ist ein Montel-Raum.
Eigenschaften von Montelräumen
- Montel-Räume sind reflexiv und daher tonneliert.
- Montel-Räume sind quasivollständig, d.h. jedes beschränkte Cauchy-Netz konvergiert. Es gibt unvollständige Montel-Räume.
- Direkte Produkte (mit der Produkttopologie) und direkte Summen (mit der Finaltopologie) von Montel-Räumen sind wieder Montel-Räume.
- Im Allgemeinen sind weder abgeschlossene Unterräume noch Quotienten von Montel-Räumen wieder Montel-Räume.
- Ist E ein Montel-Raum, so auch der starke Dualraum E'. Insbesondere sind also die in der Distributionstheorie auftretenden Räume
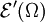 ,
, 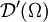 und
und 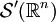 Montel-Räume.
Montel-Räume.
Quellen
- K. Floret, J. Wloka: Einführung in die Theorie der lokalkonvexen Räume, Lecture Notes in Mathematics 56, 1968
- H. H. Schaefer: Topological Vector Spaces, Springer, 1971 ISBN 0-387-98726-6
- H. Jarchow: Locally Convex Spaces, Teubner, Stuttgart 1981 ISBN 3-519-02224-9
- R. Meise, D. Vogt: Einführung in die Funktionalanalysis, Vieweg, 1992 ISBN 3-528-07262-8
Wikimedia Foundation.
