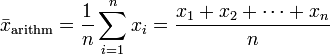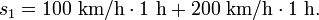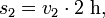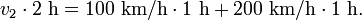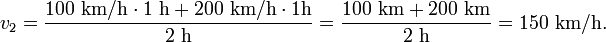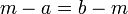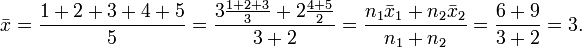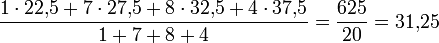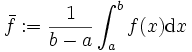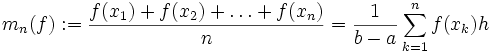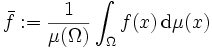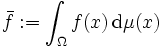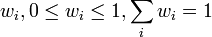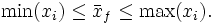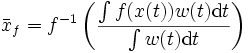Arithmetischer Mittelwert

Das arithmetische Mittel (auch Durchschnitt) ist ein Mittelwert, der folgendermaßen definiert ist:

$\bar{x}_{\mathrm{arithm}} = \frac{1}{n} \sum_{i=1}^n{x_i} = \frac{x_1 + x_2 + \cdots + x_n}{n}$

Beispiele

Das arithmetische Mittel von 50 und 100 ist $\tfrac{50+100}{2} = 75.$

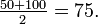
Anwendungsbeispiel

Ein Auto fährt eine Stunde lang 100 km/h und die darauf folgende Stunde 200 km/h. Mit welcher konstanten Geschwindigkeit muss ein anderes Auto fahren, um denselben Weg ebenfalls in zwei Stunden zurückzulegen?

Der Weg s₁, den das erste Auto insgesamt zurückgelegt hat, beträgt

$s_1=100\ \mathrm{km/h} \cdot 1\ \mathrm{h}+200\ \mathrm{km/h} \cdot 1\ \mathrm{h}.$

und der des zweiten Autos

$s_2=v_2 \cdot 2\ \mathrm{h},$

wobei v₂ die Geschwindigkeit des zweiten Autos ist. Aus s₁ = s₂ ergibt sich

$v_2 \cdot 2\ \mathrm{h}=100\ \mathrm{km/h} \cdot 1\ \mathrm{h}+200\ \mathrm{km/h} \cdot 1\ \mathrm{h}.$

und damit

$v_2=\frac{100\ \mathrm{km/h}\cdot 1\ \mathrm{h}+200\ \mathrm{km/h} \cdot 1\mathrm{h}}{2\ \mathrm{h}}=\frac{100\ \mathrm{km}+200\ \mathrm{km}}{2\ \mathrm{h}}=150\ \mathrm{km/h}.$

Für die Bedeutung des arithmetischen Mittelwert in der Elektrotechnik siehe Arithmetischer Mittelwert (Elektrotechnik)

Interpretationen

Arithmetisch

Das arithmetische Mittel zweier Zahlen a,b ist diejenige Zahl m, für die gilt

$\ m-a=b-m$

Wahrscheinlichkeitstheoretisch

Sind 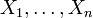$X_1, \dots, X_n$ Zufallsvariablen, die unabhängig und identisch verteilt mit Mittelwert bzw. Erwartungswert μ und Varianz σ² sind, so hat der Stichprobenmittelwert 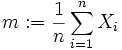$m:=\frac{1}{n}\sum_{i=1}^n X_i$ ebenfalls Mittelwert μ, aber die kleinere Varianz σ² / n. Hat also eine Zufallsvariable endlichen Mittelwert und endliche Varianz, so folgt aus der Tschebyschow-Ungleichung, dass das arithmetische Mittel einer Stichprobe gegen den Erwartungswert der Zufallsvariablen stochastisch konvergiert. Das arithmetische Mittel ist daher nach vielen Kriterien eine geeignete Schätzung für den Erwartungswert der Verteilung, aus der die Stichprobe stammt. Es ist allerdings sehr empfindlich gegenüber Ausreißern (siehe Median und Sonstige Mittelwerte).

Gewichtetes arithmetisches Mittel

Es lässt sich auch ein gewichtetes arithmetisches Mittel definieren. Es folgt diese im statistischen und im wahrscheinlichketistheortischen Sinne.

Statistik

Das gewichtete Mittel wird beispielsweise verwendet, wenn man Mittelwerte x_i, 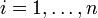$i=1,\dots, n$ aus n Stichproben der gleichen Grundgesamtheit mit verschiedenen Stichprobenumfängen w_i miteinander kombinieren will:

$\bar{x} = \frac{\sum_{i=1}^n{w_i \cdot x_i}}{\sum_{i=1}^n w_i}$.

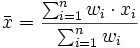Wahrscheinlichkeitsrechnung

Sind die X_i unabhängig verteilte Zufallsgrößen (d. h. X₁ ist eine Zufallsgröße mit den Zufallsvariablen 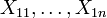$X_{11}, \dots, X_{1n}$ und X₂ ist eine Zufallsgröße mit den Zufallsvariablen 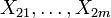$X_{21},\dots,X_{2m}$ …) mit gemeinsamem Erwartungswert μ aber unterschiedlichen Varianzen 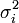$\sigma_i^2$, so hat der gewichtete Mittelwert ebenfalls Erwartungswert μ und seine Varianz beträgt

$\sigma^2_{\bar{x}} = \frac{\sum_{i=1}^n w_i^2\sigma_i^2}{\left(\sum_{i=1}^n w_i\right)^2}$.

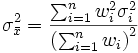Wählt man

$w_i = \frac{1}{\sigma_{i}^2}$,

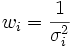so vereinfacht sich die Varianz zu

$\sigma^2_{\bar{x}} = \frac{1}{\sum_{i=1}^n\frac{1}{\sigma_i^2}}$.

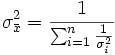Aus der Cauchy-Schwarzschen Ungleichung folgt

$\left(\sum_{i=1}^n w_i^2\sigma_i^2\right)\cdot\left(\sum_{i=1}^n\frac{1}{\sigma_i^2}\right)\geq \left(\sum_{i=1}^n w_i\right)^2$,

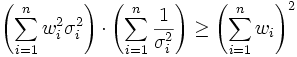die Wahl 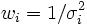$w_i = 1/\sigma_{i}^2$ oder eine Wahl proportional dazu minimiert also die Varianz des gewichteten Mittels. Mit dieser Formel lassen sich die Gewichte w_i abhängig von der Varianz des jeweiligen Wertes, der dementsprechend den Mittelwert mehr oder weniger stark beeinflusst, zweckmäßig wählen.

Sind die X_i speziell Stichprobenmittelwerte vom Umfang n_i aus derselben Grundgesamtheit, so hat X_i die Varianz σ² / n_i, also ist die Wahl w_i = n_i optimal.

Beispiele

Das arithmetische Mittel 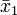$\bar{x}_1$ der n₁ = 3 Zahlen 1, 2 und 3 beträgt 2, das arithmetische Mittel 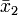$\bar{x}_2$ der n₂ = 2 Zahlen 4 und 5 beträgt 4,5. Das arithmetische Mittel aller 5 Zahlen ergibt sich als mit dem Stichprobenumfang gewichteter Mittelwert der Teilmittelwerte:

$\bar{x}=\frac{1+2+3+4+5}{5}=\frac{3\frac{1+2+3}{3}+2\frac{4+5}{2}}{3+2}=\frac{n_1\bar{x}_1+n_2\bar{x}_2}{n_1+n_2}=\frac{6+9}{3+2}=3.$

Liegen die Beobachtungen als klassierte Häufigkeit vor, kann man das arithmetische Mittel näherungsweise als gewichtetes Mittel bestimmen, wobei die Klassenmitten als Wert und der Klassenumfang als Gewicht zu wählen sind. Sind beispielsweise in einer Schulklasse ein Kind in der Gewichtsklasse 20 bis 25 kg, 7 Kinder in der Gewichtsklasse 25 bis 30 kg, 8 Kinder in der Gewichtsklasse 30 bis 35 kg und 4 Kinder in der Gewichtsklasse 35 bis 40 kg, so lässt sich das Durchschnittsgewicht als

$\frac{1 \cdot 22{,}5 + 7 \cdot 27{,}5 + 8 \cdot 32{,}5 + 4 \cdot 37{,}5}{1 + 7 + 8 + 4} = \frac{625}{20} = 31{,}25$

abschätzen.

Weiteres Beispiel: Ein Bauer stellt im Nebenerwerb 100 kg Butter her. 10 kg kann er für 10 €/kg verkaufen, weitere 10 kg für 6 €/kg und den Rest muss er für 3 €/kg verschleudern. Zu welchem (gewichtetem) Durchschnittspreis hat er seine Butter verkauft? Lösung: (10 kg · 10 €/kg + 10 kg · 6 €/kg + 80 kg · 3 €/kg) / (10 kg + 10 kg + 80 kg) = 400 € / 100 kg = 4 €/kg. Der mit der jeweils verkauften Menge gewichtete Durchschnittspreis entspricht also dem fixen Preis, zu dem die Gesamtmenge verkauft werden müsste, um den gleichen Erlös zu erzielen wie beim Verkauf von Teilmengen zu wechselnden Preisen.

Der Mittelwert einer Funktion

Als Mittelwert der Riemann-integrierbaren Funktion $f:[a,b]\to\R$ wird die Zahl

$\bar{f}:=\frac{1}{b-a}\int_a^b f(x) \mathrm{d}x$

definiert.

Die Bezeichnung Mittelwert ist insofern gerechtfertigt, als für eine äquidistante Zerlegung 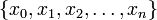$\{x_0,x_1, x_2,\dots, x_n\}$ des Intervalls mit der Schrittweite 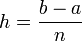$h=\frac{b-a}{n}$ das arithmetische Mittel

$m_n(f):=\frac{f(x_1)+f(x_2)+\dots +f(x_n)}{n}=\frac{1}{b-a}\sum_{k=1}^nf(x_k)h$

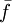gegen $\bar{f}\;$ konvergiert, vgl. ^[1].

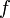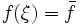Ist $f\;$ stetig, so besagt der Mittelwertsatz der Integralrechnung, dass es ein $\xi\in[a,b]$ gibt mit $f(\xi)=\bar{f}\;$, die Funktion nimmt also an mindestens einer Stelle ihren Mittelwert an.

Der Mittelwert der Funktion f(x) mit dem Gewicht 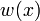$w(x)\;$ (wobei 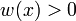$w(x)>0\;$ für alle $x \in [a,b]$) ist

$\bar{f} = \frac{\int_a^b f(t) w(t) \mathrm{d}t}{\int_a^b w(t) \mathrm{d}t}$.

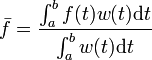Für Lebesgue-Integrale im Maßraum 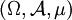$(\Omega, \mathcal A, \mu)$ mit einem endlichen Maß 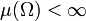$\mu(\Omega)<\infty$ lässt sich der Mittelwert einer Lebesgue-integrierbaren Funktion als

$\bar{f}:=\frac{1}{\mu(\Omega)}\int_\Omega f(x)\,\mathrm{d}\mu(x)$

definieren. Handelt es sich um einen Wahrscheinlichkeitsraum, gilt also 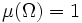$\mu(\Omega)=1\;$, so nimmt der Mittelwert die Form

$\bar{f}:=\int_\Omega f(x)\,\mathrm{d}\mu(x)$

an; das entspricht genau dem Erwartungswert von $f\;$.

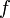Quasi-arithmetischer Mittelwert (f-Mittel)

Sei f eine auf einem reellen Intervall I streng monotone stetige (und daher invertierbare) Funktion und seien

$w_i, 0\leq w_i\leq 1, \sum_i w_i =1$

Gewichtsfaktoren. Dann ist für 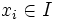$x_i\in I$ das mit den Gewichten w_i gewichtete quasi-arithmetische Mittel definiert als

$\bar{x}_f = f^{-1}\left(\sum_{i=1}^n w_i f(x_i)\right)$.

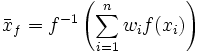Offensichtlich gilt

$\min(x_i)\leq \bar{x}_f \leq\max(x_i).$

Für f(x) = x erhält man das arithmetische, für f(x) = log(x) das geometrische Mittel, und für f(x) = x^k das k-Potenzmittel.

Dieser Mittelwert lässt sich auf das gewichtete quasi-arithmetische Mittel einer Funktion 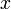$x\;$ verallgemeinern, wobei 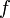$f\;$ in einem die Bildmenge von x umfassenden Intervall streng monoton und stetig sei, verallgemeinern:

$\bar{x}_f = f^{-1}\left(\frac{\int f(x(t)) w(t) \mathrm{d}t}{\int w(t) \mathrm{d}t}\right)$

Einzelnachweise

1. ↑ H. Heuser: Lehrbuch der Analysis, Teil 1, 8. Auflage, Teubner, Stuttgart 1990. ISBN 3-519-12231-6