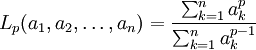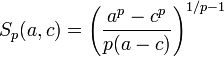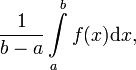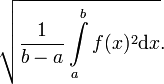- Gewichteter Mittelwert
-
Mittelwerte treten in der Mathematik und insbesondere in der Statistik in inhaltlich unterschiedlichen Kontexten auf. In der Statistik ist ein Mittelwert ein sog. Lageparameter (Überbegriff Parameter (Statistik)), also ein aggregierender Parameter einer Verteilung, einer Stichprobe oder Grundgesamtheit. Ziel solcher aggregierender Parameter ist es, die wesentliche Information in einer längeren Reihe von z. B. Messdaten in wenigen Daten zu konzentrieren.
Allgemein gilt, dass jedem Mittelwert eine Vorschrift zugrundeliegt, mit der man aus zwei Zahlen eine weitere berechnet, die zwischen den beiden gegebenen liegt.
Definitionen der bekanntesten und wichtigsten Mittelwerte
Im Folgenden seien
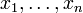 gegebene reelle Zahlen, in der Statistik etwa Messwerte, deren Mittelwert berechnet werden soll.
gegebene reelle Zahlen, in der Statistik etwa Messwerte, deren Mittelwert berechnet werden soll.Mittelwert Definition[1] Modus Ausprägung mit höchster Häufigkeit Median 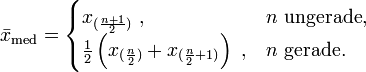
Arithmetisches Mittel 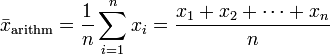
Geometrisches Mittel ![\bar{x}_\mathrm{geom} = \sqrt[n]{\prod_{i=1}^n{x_i}} = \sqrt[n]{x_1 \cdot x_2 \cdot \ldots \cdot x_n}](/pictures/dewiki/53/5db07c045b3527e85efe9055921be557.png)
Harmonisches Mittel 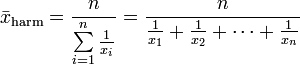
Quadratisches Mittel 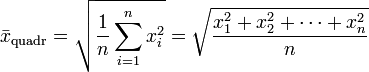
Beispiele für die Verwendung unterschiedlicher Mittelwerte
Urliste Wert x(1) 2 (A) x(2) 2 (A) x(3) 2 (A) x(4) 3 (B) x(5) 3 (B) x(6) 4 (C) x(7) 5 (D) Im Folgenden soll beispielhaft an den sieben rechts angegebenen Ausprägungen gezeigt werden, wo welche Definition des Mittelwerts sinnvoll ist.
Der Modus ist bereits in der Nominalskala sinnvoll, in der einzelne Merkmale nicht geordnet werden können. Sind etwa von sieben befragten Personen drei katholisch (
 A), zwei evangelisch (
A), zwei evangelisch ( B), einer muslimisch (
B), einer muslimisch ( C) und einer Hindu (
C) und einer Hindu (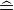 D), so liegt der Modus bei A, denn dies kommt am häufigsten vor.
D), so liegt der Modus bei A, denn dies kommt am häufigsten vor.Für den Median ist eine Ordinalskala Voraussetzung, in der die Merkmale geordnet werden können. Auf die Frage nach der Qualität des Essens eines Restaurants antworten beispielsweise drei Kunden mit "sehr gut" (
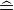 A), zwei mit "gut" (
A), zwei mit "gut" (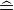 B) sowie je einer mit "mittel" und "schlecht" (
B) sowie je einer mit "mittel" und "schlecht" (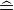 C und D). Nach Ordnen der Daten wie in der Liste rechts erkennt man, dass die mittlere Beobachtung bei x(4) liegt. Der Median ist also B.
C und D). Nach Ordnen der Daten wie in der Liste rechts erkennt man, dass die mittlere Beobachtung bei x(4) liegt. Der Median ist also B.Das arithmetische Mittel wird beispielsweise zum Berechnen der Durchschnittsgeschwindigkeit genutzt: Läuft eine Schildkröte erst drei Meter pro Stunde, dann drei Stunden lang je zwei Meter und beschleunigt für jeweils eine Stunde nochmals auf drei, vier und fünf Meter pro Stunde, so ergibt sich als arithmetisches Mittel:
Auch das harmonische Mittel kann zur Berechnung einer durchschnittlichen Geschwindigkeit sinnvoll sein, wenn nicht stündlich sondern nach Strecke gemessen wird: Die Schildkröte laufe den ersten Meter mit drei Metern pro Stunde, weitere drei Meter mit jeweils 2 m/h und beschleunigt auf den letzten drei Metern nochmals auf jeweils drei, vier und fünf m/h. Die Schildkröte braucht somit 157/60 Stunden für sieben Meter, denn
Daraus ergibt sich dann die Durchschnittsgeschwindigkeit von 2,68 Metern pro Stunde.
Mit dem geometrischen Mittel errechnet man den mittleren Wachstumsfaktor. Eine Bakterienkultur wachse beispielsweise am ersten Tag um das Fünffache, am zweiten um das Vierfache, dann zweimal um das Dreifache und die letzten drei Tage verdoppelt sie sich täglich. Der Bestand nach dem siebten Tag errechnet sich also durch
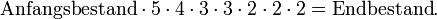 Alternativ kann mit dem geometrischen Mittel der Endbestand ermittelt werden, denn
Alternativ kann mit dem geometrischen Mittel der Endbestand ermittelt werden, dennund somit ist
Ein tägliches Wachstum der Bakterienkultur um das 2,83-fache hätte also nach sieben Tagen zum selben Ergebnis geführt.
Geschichte
In der Mathematik treten Mittelwerte, insbesondere die drei klassischen Mittelwerte (Arithmetisches, Geometrisches und Harmonisches Mittel) bereits in der Antike auf. Pappos von Alexandria kennzeichnet 10 verschiedene Mittelwerte m von 2 Zahlen a und b (a < b) durch spezielle Werte des Streckenverhältnisses (b − m):(m − a). Auch die Ungleichung zwischen harmonischem, geometrischem und arithmetischem Mittel ist in der Antike bereits bekannt und geometrisch interpretiert. Im 19. und 20. Jahrhundert spielen Mittelwerte in der Analysis eine spezielle Rolle, dort im Wesentlichen im Zusammenhang mit berühmten Ungleichungen und wichtigen Funktionseigenschaften wie Konvexität (Hölder-Ungleichung, Minkowski-Ungleichung, Jensensche Ungleichung usw.). Dabei wurden die klassischen Mittelwerte in mehreren Schritten verallgemeinert, zunächst zu den Potenzmittelwerten und diese wiederum zu den quasi-arithmetischen Mittelwerten. Die klassische Ungleichung zwischen harmonischem, geometrischem und arithmetischem Mittel geht dabei über in allgemeinere Ungleichungen zwischen Potenzmittelwerten bzw. quasi-arithmetischen Mittelwerten.
Gemeinsame Definition der drei klassischen Mittelwerte
Die Idee, die den drei klassischen Mittelwerten zugrunde liegt, lässt sich auf folgende Weise allgemein formulieren:
Beim arithmetischen Mittel sucht man die Zahl m, für die gilt:
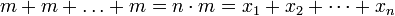 ,
,
wobei sich die Summe links über n Summanden erstreckt. Das arithmetische Mittel mittelt also bzgl. der arithmetischen Verknüpfung „Summe“. Anschaulich bestimmt man mit dem arithmetischen Mittel aus Stäben verschiedener Länge einen mit einer durchschnittlichen oder mittleren Länge.
Beim geometrischen Mittel sucht man die Zahl m, für die gilt:
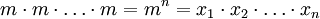 ,
,
wobei sich das Produkt links über n Faktoren erstreckt. Das geometrische Mittel mittelt also bzgl. der arithmetischen Verknüpfung „Produkt“.
Das harmonische Mittel m löst die Gleichung
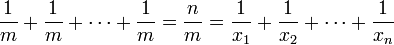 .
.
Zusammenhänge
Die Mittelwerte hängen untereinander in verschiedenen Weisen zusammen; z.B. ist
oder nach dem geometrischen Mittel aufgelöst
Außerdem ist der Kehrwert des harmonischen Mittels gleich dem arithmetischen Mittel der Kehrwerte der Zahlen.
Ungleichung der Mittelwerte
- Hauptartikel: Ungleichung der Mittelwerte
Die Ungleichung von arithmetischen und geometrischen Mittel vergleicht die Wert des arithmetischen und geometrischen Mittels zweier gegebener Zahlen: Es gilt stets
Die Ungleichung lässt sich auch auf weitere Mittelwerte ausdehnen, z.B. (für positive Variable):
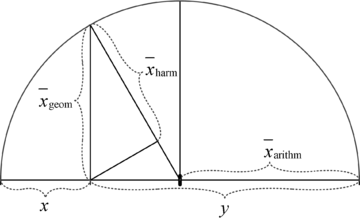
Für zwei (positive) Variable gibt es auch eine grafische Veranschaulichung:
Das geometrische Mittel folgt direkt aus dem euklidischen Höhensatz und das harmonische Mittel aus dem euklidischen Kathetensatz mit der Beziehung
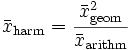 .
.
Weitere Mittelwerte und ähnliche Funktionen
Gewichtete Mittel
Die gewichteten Mittelwerte entstehen, wenn man den einzelnen Werte unterschiedliche Gewichte, mit denen sie in das Gesamtmittel einfließen, zuordnet; zum Beispiel wenn bei einer Prüfung mündliche und schriftliche Leistung unterschiedlich stark in die Gesamtnote einfließen.
Die genauen Definitionen finden sich hier: gewichtetes arithmetisches Mittel, gewichtetes geometrisches Mittel, gewichtetes harmonisches Mittel
Logarithmischer Mittelwert
Der logarithmische Mittelwert
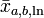 zwischen xa und xb ist definiert als:
zwischen xa und xb ist definiert als:Der logarithmische Mittelwert wird beispielsweise bei der verfahrenstechnischen Auslegung von Packungskolonnen genutzt. Er dient dort zur Mittelung der molaren Zusammensetzungen an Kopf und Boden der Kolonne .
Für
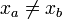 liegt der logarithmische Mittelwert zwischen dem geometrischen und dem arithmetischen Mittelwert:
liegt der logarithmische Mittelwert zwischen dem geometrischen und dem arithmetischen Mittelwert:Es gibt auch eine Verallgemeinerung des logarithmischen Mittelwerts auf mehr als zwei Variablen[2].
Winsorisiertes oder gestutztes Mittel
Kann man davon ausgehen, dass die Daten durch „Ausreißer“, d. h. einige wenige zu hohe oder zu niedrige Werte kontaminiert sind, so sortiert man die Beobachtungswerte nach aufsteigender Größe, schneidet eine gleiche Anzahl von Werten am Anfang und am Ende der Folge ab und berechnet von den übrig bleibenden Werten den Mittelwert. Ein 10 % winsorisiertes Mittel erhält man, wenn man 5 % der Gesamtzahl aller Werte am unteren und 5 % am oberen Ende auslässt.
Das „a-Mittel“
Für einen gegebenen reellen Vektor
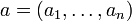 mit
mit 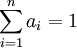 wird der Ausdruck
wird der Ausdruckwobei über alle Permutationen σ von
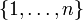 summiert wird, als „a-Mittel“ [a] der nichtnegativen reellen Zahlen x1, …, xn bezeichnet.
summiert wird, als „a-Mittel“ [a] der nichtnegativen reellen Zahlen x1, …, xn bezeichnet.Für den Fall
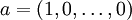 , ergibt das genau das arithmetische Mittel der Zahlen x1, …, xn; für den Fall
, ergibt das genau das arithmetische Mittel der Zahlen x1, …, xn; für den Fall 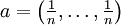 ergibt sich genau das geometrische Mittel.
ergibt sich genau das geometrische Mittel.Für die a-Mittel gilt die Muirhead-Ungleichung.
Beispiel: Sei
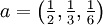 und
und 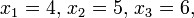 dann gilt
dann gilt 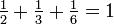 und die Menge der Permutationen (in Kurzschreibweise) von
und die Menge der Permutationen (in Kurzschreibweise) von 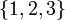 ist
istDamit ergibt sich
Gleitende Durchschnitte
- Hauptartikel: Gleitender Mittelwert
Gleitende Durchschnitte werden in der dynamischen Analyse von Messwerten angewandt. Sie sind außerdem ein gängiges Mittel der technischen Analyse in der Finanzmathematik. Mit gleitenden Durchschnitten kann das stochastische Rauschen aus zeitlich voranschreitenden Signalen herausgefiltert werden. Häufig handelt es sich dabei um FIR-Filter. Jedoch muss beachtet werden, dass die meisten gleitenden Durchschnitte dem echten Signal hinterherlaufen. Für vorausschauende Filter siehe z. B. Kalman-Filter.
Gleitende Durchschnitte benötigen normalerweise eine unabhängige Variable, die die Größe der nachlaufenden Stichprobe bezeichnet, bzw. das Gewicht des vorangehenden Wertes für die exponentiellen gleitenden Durchschnitte.
Gängige gleitende Durchschnitte sind:
- Arithmetische gleitende Durchschnitte (Simple Moving Average, SMA)
- Exponentiell gleitende Durchschnitte (Exponential Moving Average, EMA)
- Doppelt exponentiell gleitende Durchschnitte (Double EMA, DEMA)
- Dreifach, n-fach exponentiell gleitende Durchschnitte (Triple EMA, TEMA)
- Linear gewichtete gleitende Durchschnitte (linear abfallende Gewichtung)
- Quadratisch gewichtete gleitende Durchschnitte
- Weitere Gewichtungen: Sinus, Triangular, …
In der Finanzliteratur können außerdem sogenannte adaptive gleitende Durchschnitte gefunden werden, die sich automatisch einer sich ändernden Umgebung (andere Volatilität/Streuung etc.) anpassen:
- Kaufmann’s adaptive moving average (KAMA)
- Variable Index Dynamic Average (VIDYA)
Für die Anwendung von gleitenden Durchschnitten siehe auch Gleitende Durchschnitte (Chartanalyse) und MA-Modell.
Sonstige Mittelwerte
Sonstige Mittelwerte, die in einem eigenen Artikel beschrieben werden, sind der Modus (eigentlich kein Mittelwert, sondern der häufigste Wert) und der Median, der robust gegenüber extremen Abweichungen, sogenannten Ausreißern, ist.
Außerdem lassen sich Mittelwerte kombinieren; so entsteht etwa das arithmetisch-geometrische Mittel, das zwischen dem arithmetischen und geometrischen Mittel liegt.
Verallgemeinerte Mittelwerte
Es gibt eine Reihe weiterer Funktionen, mit denen sich die bekannten und weitere Mittelwerte erzeugen lassen.
Hölder-Mittel
Für positive Zahlen xi definiert man den k-Potenzmittelwert, auch Hölder-Mittel[3] (engl.: k-th power mean) als
Die Notation ist nicht einheitlich, alternativ sind auch Schreibweisen wie Mk(x), mk(x) oder μk(x) üblich. Genauso wie die Schreibweise ist auch die Bezeichnungsweise uneinheitlich; möglich sind Varianten wie k-tes Mittel, Mittel der Ordnung oder vom Grad k oder Mittel mit Exponent k.
Mittels geeigneter Wahl des Parameters k können unter anderem die drei obigen Mittelwerte erzeugt werden:
- k = − 1: Harmonisches Mittel,
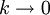 : Geometrisches Mittel,
: Geometrisches Mittel,- k = 1: Arithmetisches Mittel,
- k = 2: Quadratisches Mittel oder Effektivwert (in der Elektrotechnik),
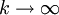 :
: 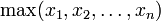 ,
,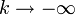 :
: 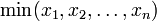 .
.
Außerdem gilt: Je größer k ist, desto größer ist Mk; daraus folgt dann die verallgemeinerte Ungleichung der Mittelwerte
Die Potenzmittelwerte stehen über die einfache Formel
mit den Stichprobenmomenten mk um Null in Beziehung. Außerdem wird in der Stochastik die Konvergenz im p-ten Mittel über diese Potenzmittelwerte definiert.
Lehmer-Mittel
Das Lehmer-Mittel[4] ist eine anderer verallgemeinerter Mittelwert; zur Stufe p ist es definiert durch
Es hat die Spezialfälle
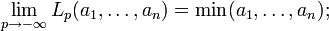
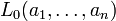 ist das harmonische Mittel;
ist das harmonische Mittel;- L1 / 2(a1,a2) ist das geometrische Mittel von a1 und a2;
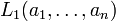 ist das arithmetische Mittel;
ist das arithmetische Mittel;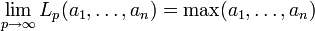 .
.
Stolarsky-Mittel
Das Skolarsky-Mittel[5] zweier Zahlen a,c ist definiert durch
Mittelwert einer Funktion
Das arithmetische Mittel einer stetigen Funktion f(x) in einem geschlossenen Intervall [a,b] ist
ihr quadratisches
Siehe auch
Literatur
- F. Ferschl: Deskriptive Statistik. 3. Auflage. Physica-Verlag Würzburg, ISBN 3-7908-0336-7.
- P. S. Bullen: Handbook of Means and Their Inequalities, Kluwer Acad. Pub. 2003, ISBN 1-402-01522-4. (umfassende Diskussion von Mittelwerten und der mit ihnen verbundenen Ungleichungen)
- G. H. Hardy, J. E. Littlewood, G. Polya: Inequalities, Cambridge Univ. Press 1964.
- E. Beckenbach, R. Bellman: Inequalities, Springer, Berlin 1961.
Weblinks
- Averaging auf Scholarpedia
- "Geometrisches Mittel" zweier Werte und im Vergleich dazu "Arithmetisches Mittel"
Einzelnachweise
- ↑ F. Ferschl: Deskriptive Statistik. 3. Auflage. Physica-Verlag Würzburg, ISBN 3-7908-0336-7. Seiten 48-74
- ↑ A. O. Pittenger: The logarithmic mean in n variables. In: Amer. Math. Monthly, 92 (1985), S. 99–104.
- ↑ http://members.chello.at/gut.jutta.gerhard/newsletter/newsletter14.htm
- ↑ Eric W. Weisstein: Lehmer Mean auf MathWorld (englisch)
- ↑ Eric W. Weisstein: Stolarsky Mean auf MathWorld (englisch)
Wikimedia Foundation.

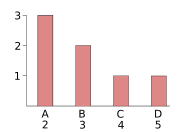
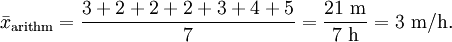
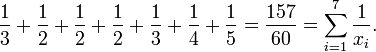
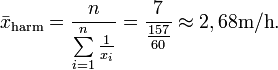
![\bar{x}_\mathrm{geom} = \sqrt[7]{5 \cdot 4 \cdot 3 \cdot 3 \cdot 2 \cdot 2 \cdot 2} = \sqrt[7]{1440} \approx 2,83](/pictures/dewiki/57/96b5b064ffe92999fa201688fba0fed8.png)
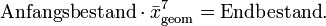
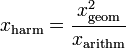
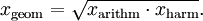
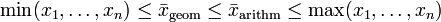
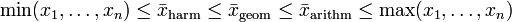
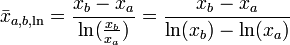
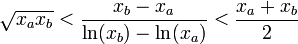
![[a]={1 \over n!}\sum_\sigma x_{\sigma(1)}^{a_1}\cdots x_{\sigma(n)}^{a_n},](/pictures/dewiki/99/ce19ed9f30d8835cb544968b22a79614.png)
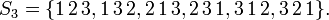
![\begin{align}
{[a]} &amp;amp; = {1 \over 3!}\left(x_1^{\frac 1 2}x_2^{\frac 1 3}x_3^{\frac 1 6}+x_1^{\frac 1 2}x_3^{\frac 1 3}x_2^{\frac 1 6}+x_2^{\frac 1 2}x_1^{\frac 1 3}x_3^{\frac 1 6}+x_2^{\frac 1 2}x_3^{\frac 1 3}x_1^{\frac 1 6}+x_3^{\frac 1 2}x_1^{\frac 1 3}x_2^{\frac 1 6}+x_3^{\frac 1 2}x_2^{\frac 1 3}x_1^{\frac 1 6}\right) \\
&amp;amp; = {1 \over 6}\left(4^{\frac 1 2}{\cdot}5^{\frac 1 3}{\cdot}6^{\frac 1 6}+4^{\frac 1 2}{\cdot}6^{\frac 1 3}{\cdot}5^{\frac 1 6}+5^{\frac 1 2}{\cdot}4^{\frac 1 3}{\cdot}6^{\frac 1 6}+5^{\frac 1 2}{\cdot}6^{\frac 1 3}{\cdot}4^{\frac 1 6}+6^{\frac 1 2}{\cdot}4^{\frac 1 3}{\cdot}5^{\frac 1 6}+6^{\frac 1 2}{\cdot}5^{\frac 1 3}{\cdot}4^{\frac 1 6}\right) \\
&amp;amp; \approx 4{,}94.
\end{align}](/pictures/dewiki/97/a0e0cdd7b15ef337f0390943c7ca85ec.png)
![\bar{x}(k) = \sqrt[k]{\frac{1}{n}\sum_{i=1}^n{x_i^k}}](/pictures/dewiki/49/17f2edfaceb8c438be3fe865bd08aaa1.png)
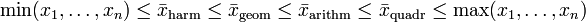
![\bar{x}(k)=\sqrt[k]{m_k}](/pictures/dewiki/97/ae57a31a0a77d7842500e42ef32f6bf8.png)