Transzendent (Mathematik)

Statue Al-Chwarizmis, Al-Khwarizmi, Technische Universität Teheran

Die Algebra ist eines der grundlegenden Teilgebiete der Mathematik, das sich der Struktur, Relation und der Menge widmet. Im Volksmund wird Algebra häufig als das Rechnen mit Unbekannten in Gleichungen bezeichnet (zum Beispiel x + 10 = 20).

Wortgeschichte

Eine der ersten Darstellungen der Algebra ist das Aryabhattiya, ein mathematisches Lehrbuch des indischen Mathematikers Aryabhata aus dem 5. Jahrhundert; die verwendete Methodik wurde Bijaganitam genannt. Im 13. Jahrhundert übernahmen und verfeinerten die Iraner diese Methode, die sie al-ǧabr (von arab.: „das Ergänzen“/„das Einrichten“) nannten. Der Begriff ist aus dem Titel des Rechen-Lehrbuchs al-Kitab al-mukhtasar fi hisab al-dschabr wa-l-muqabala („Das kurz gefasste Buch über die Rechenverfahren durch Ergänzen und Ausgleichen“) des persischen Mathematikers al-Chwarizmi entnommen. Vier Jahrhunderte nach der Publikation des Buches erschien seine lateinische Übersetzung Ludus algebrae et almucgrabalaeque. Aus „al-ǧabr“ entwickelte sich das heutige Wort „Algebra“.

Algebra als Teilgebiet der Mathematik: Begriffsbestimmung und Gliederung

Die Inhalte und Methoden der Algebra haben sich im Laufe der Geschichte so stark erweitert, dass es schwer geworden ist, den Begriff der Algebra in einer knappen Definition anzugeben. Weiterhin wäre es nicht praktikabel, alle Aspekte der Algebra in einem Enzyklopädie-Artikel zu behandeln. Wir unterscheiden deshalb folgende, keineswegs scharf voneinander abgegrenzte Teilgebiete:

• Die elementare Algebra ist die Algebra im Sinne der Schulmathematik. Sie umfasst die Rechenregeln der natürlichen, ganzen, gebrochenen und reellen Zahlen, den Umgang mit Ausdrücken, die Variablen enthalten, und Wege zur Lösung einfacher algebraischer Gleichungen.
• Die klassische Algebra beschäftigt sich mit dem Lösen allgemeiner algebraischer Gleichungen (siehe unten) über den reellen oder komplexen Zahlen. Ihr zentrales Resultat ist der Fundamentalsatz der Algebra, der besagt, dass jedes nichtkonstante Polynom n-ten Grades in n Linearfaktoren mit komplexen Koeffizienten zerlegt werden kann.
• Die abstrakte Algebra ist eine Grundlagendisziplin der modernen Mathematik. Sie beschäftigt sich mit speziellen algebraischen Strukturen wie Gruppen, Ringen, Körpern und deren Verknüpfung.
• Die lineare Algebra behandelt das Lösen linearer Gleichungssysteme, die Untersuchung von Vektorräumen und die Bestimmung von Eigenwerten; sie ist Grundlage für die analytische Geometrie.
• Die multilineare Algebra handelt von Tensoren.
• Die kommutative Algebra befasst sich mit kommutativen Ringen sowie deren Idealen, Moduln und Algebren.
• Die reelle Algebra untersucht algebraische Zahlkörper, auf denen eine Anordnung definiert werden kann. Weiter werden darauf positive Polynome untersucht.
• Die Computer-Algebra beschäftigt sich mit der symbolischen Manipulation algebraischer Ausdrücke. Einen Schwerpunkt bildet das exakte Rechnen mit ganzen, rationalen und algebraischen Zahlen sowie mit Polynomen über diesen Zahlenräumen. Auf der theoretischen Seite ist diesem Teilgebiet die Suche nach effizienten Algorithmen sowie die Ermittlung der Komplexität dieser Algorithmen zuzuordnen. Auf der praktischen Seite wurde eine Vielzahl von Computeralgebrasystemen entwickelt, die die rechnergestützte Manipulation algebraischer Ausdrücke ermöglichen.
• Die universelle oder allgemeine Algebra betrachtet ganz allgemein algebraische Strukturen.

Algebra als mathematische Struktur

Als universelle oder allgemeine Algebra, kurz Algebra, wird das Grundkonstrukt einer algebraischen Struktur bezeichnet: Eine (meist nichtleere) Menge, auf der eine oder mehrere (u.U. partielle) Verknüpfungen („Operationen“ genannt) definiert sind und in der gewisse Axiome gelten. Gruppen, Ringe, Körper sind somit Beispiele für spezielle Algebren.

„Algebra“ bezeichnet konkrete algebraische Strukturen, die Verallgemeinerungen des Ringbegriffes sind, siehe Algebra (Struktur).

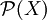• Eine Mengenalgebra, manchmal Algebra genannt, ist eine Teilmenge $\mathcal A$ einer Potenzmenge $\mathcal P(X)$ von einer Menge X mit Vereinigung und Komplementbildung als Verknüpfungen und der axiomatischen Forderung $X \in \mathcal A$.
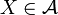• Eine σ-Algebra ist eine Mengenalgebra, die unter abzählbar unendlichen Vereinigungen abgeschlossen ist. σ-Algebren bilden eine Grundlage der Maßtheorie.
• Boolesche Algebra
• Siehe Relationale Algebra - ist Grundlage für Datenbanken
• assoziative Algebra
• Clifford-Algebra
• Lie-Algebra
• Jordan-Algebra
• Banach-Algebra
• Divisionsalgebra
• Hopf-Algebra
• Graßmann-Algebra

„Algebraisch“ als Attribut von Zahlen, Funktionen, Gleichungen

Algebraisch als mathematisches Attribut hat folgende Bedeutungen:

• Eine algebraische Gleichung ist eine Gleichung, zu deren Formulierung nur endlich viele elementare Rechenoperationen (Addition, Subtraktion, Multiplikation, Division) erforderlich sind, in der also zum Beispiel keine typischen analytischen Funktionen vorkommen.
• Die algebraischen Zahlen sind die Nullstellen von Polynomen mit rationalen Koeffizienten; die Menge der algebraischen Zahlen bildet den algebraischen Abschluss der Menge der rationalen Zahlen.
• Das algebraische Element erweitert den Begriff der algebraischen Zahl auf Nullstellen von Polynomen mit Koeffizienten aus einem beliebigen vorgegebenen Körper.

„Algebraische“ Teilgebiete der Mathematik

• Algebraische Geometrie
• Algebraische Zahlentheorie
• Algebraische Topologie
• Homologische Algebra

Siehe auch

• Assoziativgesetz
• Kommutativgesetz
• Distributivgesetz
• Mathematik

Literatur

• Heinz-Wilhelm Alten et al.: 4000 Jahre Algebra. Springer-Verlag, Berlin Heidelberg 2003, ISBN 3-540-43554-9
• Siegfried Bosch: Algebra. 6. Auflage, Springer-Verlag, 2006, ISBN 978-3-540-29880-9
  Sehr Umfangreiches Lehrbuch mit ausführlichen Beweisen und Übungsaufgaben.
• G. Fischer, R. Sacher: Einführung in die Algebra, Teubner Studienbücher, Stuttgart 1983 (behandelt die abstrakte Algebra), ISBN 3-519-22053-9
• Jacob Klein: Die griechische Logistik und die Entstehung der Algebra in: Quellen und Studien zur Geschichte der Mathematik, Astronomie und Physik, Abteilung B: Studien, Band 3, Erstes Heft, Berlin 1934, p. 18-105 und Zweites Heft, Berlin 1936, p. 122-235; wiederveröffentlicht in englischer Sprache unter dem Titel: Greek Mathematical Thought and the Origin of Algebra. Cambridge, Mass. 1968, ISBN 0-486-27289-3
• Hans Kreul, Harald Ziebarth: Mathematik leicht gemacht, Verlag Harri Deutsch, 6. Auflage 2006. (Grundlagen der Algebra / keine wesentlichen Vorkenntnisse notwendig, sehr verständlich), ISBN 978-3-8171-1786-4
• Lothar Kusch: Algebra, Geometrie, Integral/Differentialrechnung. ISBN 3-590-82585-5, ISBN 3-590-82623-1, ISBN 3-590-82607-X, ISBN 3-590-82771-8
• Serge Lang: Algebra. Revised 3rd Edition, Springer-Verlag, 2002, ISBN 0-387-95385-X
  Umfangreiches Standardwerk mit vielen weiterführenden Anmerkungen und Aufgaben. Die Darstellung ist für einen ersten Einstieg möglicherweise zu abstrakt.
• B. L. van der Waerden: Algebra I, II. Springer-Verlag, Berlin 1993, ISBN 3-540-56801-8
  Der Klassiker, dessen erste Ausgaben in den 1930er Jahren noch den Titel Moderne Algebra trugen und der erstmals konsequent den axiomatischen Ansatz von E. Noether darstellte. In der Sprache inzwischen etwas veraltet.

Weblinks

• Klassische Algebra Freiberger Web-Vorlesung
• Ancient Greek Algebra
• Vaughan Pratt: Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)Vorlage:SEP/Wartung/Parameter 1 und Parameter 3 und nicht Parameter 2