NDEA

Ein nichtdeterministischer endlicher Automat (NEA, engl: NFA=nondeterministic finite automaton) ist ein endlicher Automat, bei dem es für den Zustandsübergang mehrere Möglichkeiten gibt.

Formal kann ein NEA 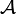$\mathcal{A}$ als 5-Tupel 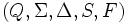$\left( Q, \Sigma, \Delta, S, F \right)$ definiert werden. Hierbei gilt Folgendes:

• Q ist eine endliche Menge von Zuständen ($\left| Q \right| < \infty$).
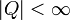• Σ ist das Eingabealphabet. $\left| \Sigma \right| < \infty$, $Q \cap \Sigma = \varnothing$
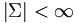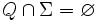
• Es gibt eine Übergangsrelation 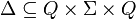$\Delta \subseteq Q \times \Sigma \times Q$. Der wesentliche Unterschied des NEA zum deterministischen endlichen Automaten (DEA) liegt somit darin, dass auch mehrere Folgezustände möglich sind, aber auch fehlen können.
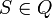• $S \in Q$ ist der Startzustand.
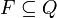• $F \subseteq Q$ ist eine (endliche) Menge möglicher akzeptierender Zustände (Finalzustände). Wenn der Automat nach Lesen des Eingabewortes 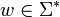$w \in \Sigma^*$ in einem Zustand aus F hält, so gehört w zur Sprache $L\left(A\right)$.

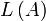NEAs, DEAs und Typ-3-Grammatiken (vgl. Chomsky-Hierarchie) beschreiben die gleiche Sprachklasse. NEAs lassen sich mittels Potenzmengenkonstruktion in äquivalente DEAs umwandeln.

Der wesentliche Unterschied des NEA zum deterministischen endlichen Automaten (DEA) liegt somit darin, dass auch mehrere Folgezustände möglich sind oder auch ganz fehlen können.

Ferner ist bei einem NEA auch ein Zustandsübergang möglich, ohne dabei ein Eingabezeichen zu verbrauchen. Diese Zustandswechsel werden als lambda-Übergänge oder epsilon-Übergänge bezeichnet und üblicherweise mit einem kleinen griechischen λ oder ε gekennzeichnet.

Um einen regulären Ausdruck in einen NEA zu überführen, sind gewisse Regeln zu befolgen, die in ^[1] genauer erläutert werden. Diesen Vorgang nennt man Induktive Konstruktion oder auch Thompson's Konstruktion.^[2]

Siehe auch

• Potenzautomat
• Eindeutiger endlicher Automat

Referenzen

1. ↑ Hans Werner Lang: http://www.inf.fh-flensburg.de/lang/theor/regulaerer-ausdruck-zu-automat-bottomup.htm
2. ↑ Aho, A. V., Sethi, R., Ullman, J. D.: Compilers: Principles, Techniques and Tools. Addison Wesley (1986)

Literatur

• John E. Hopcroft u. Jeffrey D. Ullman, Einführung in die Automatentheorie, Formale Sprachen und Komplexitätstheorie, ISBN 3-89319-181-X
• Sander/Stucky/Herschel, Automaten, Sprachen, Berechenbarkeit, ISBN 3-519-02937-5
• Gottfried Vossen, Kurt-Ulrich Witt, Grundkurs Theoretische Informatik 3.Auflage, ISBN 3-528-23147-5

Weblinks

• Artikel zum Themengebiet von Hans Werner Lang
• Beschreibung von Helmut Richter