Nakayama lemma — In mathematics, more specifically modern algebra and commutative algebra, Nakayama s lemma also known as the Krull–Azumaya theorem[1] governs the interaction between the Jacobson radical of a ring (typically a commutative ring) and its finitely… … Wikipedia
Nakayama — is a transliteration of 中山. For other transliterations, see 中山 (disambiguation). Nakayama (中山) may refer to: Nakayama, Ehime, a town in Ehime Prefecture Nakayama, Tottori, a town in Tottori Prefecture Nakayama, Yamagata, a town in Yamagata… … Wikipedia
Nakayama Tadashi — Tadashi Nakayama, oder Tadasi Nakayama, (jap. 中山 正, Nakayama Tadashi; * Juli 1912 in der Präfektur Tokio; † 1964 in Nagoya) war ein japanischer Mathematiker, der sich mit Algebra beschäftigte. Leben und Wirken Tadashi Nakayama machte 1935 seinen… … Deutsch Wikipedia
Nakayama — ist der Familienname folgender Personen: Akinori Nakayama (* 1943), japanischer Kunstturner Chikako Nakayama (* 1975), japanische Badmintonspielerin David Nakayama (* 1978), amerikanischer Comiczeichner Eiko Nakayama (* 1970), japanische… … Deutsch Wikipedia
Lemma von Nakayama — Das Lemma von Nakayama, benannt nach dem japanischen Mathematiker Tadashi Nakayama, ist der folgende Satz der kommutativen Algebra[1]: Es sei M ein endlich erzeugter nichttrivialer R Modul und ein Ideal, das im Jacobson Radikal von R liegt. Dann… … Deutsch Wikipedia
Lemma (mathematics) — In mathematics, a lemma (plural lemmata or lemmascite book |last= Higham |first= Nicholas J. |title= Handbook of Writing for the Mathematical Sciences |publisher= Society for Industrial and Applied Mathematics |year= 1998 |isbn= 0898714206 |pages … Wikipedia
Tadashi Nakayama — Tadashi Nakayama, oder Tadasi Nakayama, (jap. 中山 正, Nakayama Tadashi; * 26. Juli 1912 in der Präfektur Tokio; † 5. Juni 1964 in Nagoya) war ein japanischer Mathematiker, der sich mit Algebra beschäftigte. Leben und Wirken Tadashi Nakayama machte… … Deutsch Wikipedia
Tadashi Nakayama (mathematician) — Tadashi Nakayama (1912 Tokyo ndash;1964 Nagoya) was a mathematician who made important contributions to representation theory. He received his degrees from Tokyo University and Osaka University and held permanent positions at Osaka University and … Wikipedia
List of lemmas — This following is a list of lemmas (or, lemmata , i.e. minor theorems, or sometimes intermediate technical results factored out of proofs). See also list of axioms, list of theorems and list of conjectures. 0 to 9 *0/1 Sorting Lemma ( comparison… … Wikipedia
List of mathematics articles (N) — NOTOC N N body problem N category N category number N connected space N dimensional sequential move puzzles N dimensional space N huge cardinal N jet N Mahlo cardinal N monoid N player game N set N skeleton N sphere N! conjecture Nabla symbol… … Wikipedia
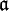 ein Ideal, das im Jacobson-Radikal von R liegt. Dann ist
ein Ideal, das im Jacobson-Radikal von R liegt. Dann ist 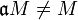 .
. ein minimales Erzeugendensystem von M. Wir nehmen
ein minimales Erzeugendensystem von M. Wir nehmen 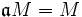 an.
an.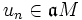 gäbe es dann eine Gleichung der Form
gäbe es dann eine Gleichung der Form 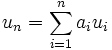 mit
mit 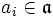 , also
, also 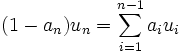 .
.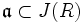 ein Ideal, so gilt
ein Ideal, so gilt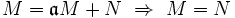 .
.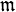 sein maximales Ideal und
sein maximales Ideal und 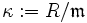 der Restklassenkörper.
der Restklassenkörper.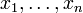 Urbilder einer Basis des κ-Vektorraums
Urbilder einer Basis des κ-Vektorraums 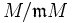 , so erzeugen die xi den Modul M.
, so erzeugen die xi den Modul M.