Nashgleichgewicht

Das Nash-Gleichgewicht, teils auch (wie im Englischen) Nash-Equilibrium genannt, ist ein zentraler Begriff der mathematischen Spieltheorie. Es beschreibt in nicht-kooperativen Spielen einen Zustand eines strategischen Gleichgewichts, von dem ausgehend kein einzelner Spieler für sich einen Vorteil erzielen kann, indem er einseitig von seiner Strategie abweicht. Es ist ein grundlegendes Lösungskonzept der Spieltheorie. Definition und Existenzbeweis des Nash-Gleichgewichts gehen auf die 1950 veröffentlichte Dissertation des Mathematikers John Forbes Nash Jr. zurück^[1].

Idee des Nash-Gleichgewichts

Das wesentliche Ziel der mathematischen Spieltheorie ist es, für Konfliktsituationen rationale Entscheidungen zu charakterisieren und zu bestimmen. Die Schwierigkeit dabei ist, dass keiner der Entscheider („Spieler“) weiß, wie sich die anderen Spieler entscheiden werden. Damit ist es für einen einzelnen Spieler völlig ungewiss, wie sich seine konkrete Entscheidung für einen Handlungsplan („Strategie“) auswirken wird.

Dem Nash-Gleichgewicht liegt nun die folgende Idee zugrunde: Man geht von allen möglichen Kombinationen aus, die für jeden Spieler eine Strategie beinhalten. Einer solchen Stategie-Kombination kann dann eine gewisse Stabilität unterstellt werden, wenn kein einzelner Spieler einen Anreiz besitzt, von seiner Strategie abzuweichen (die Auszahlung an den Spieler, der seine Strategie als Einzelner ändert, darf sich also aufgrund dieser Änderung nicht erhöhen). Ist dies der Fall, wird die betreffende Strategie-Kombination Nash-Gleichgewicht genannt.

Nash-Gleichgewichte sind im Allgemeinen nicht eindeutig bestimmt. Allerdings kann die Existenz gesichert werden, wenn der Entscheidungsrahmen der Spieler auf so genannte gemischte Strategien erweitert wird, bei denen jeder Spieler seinen Handlungsplan zufällig „auswürfeln“ darf.

Formale Definition

Reine Strategien

Es bezeichne Σ_i die Menge der Strategien (Handlungsalternativen) des i-ten Spielers und 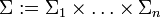$\Sigma := \Sigma_1\times\ldots\times\Sigma_n$ das kartesische Produkt dieser Strategienmengen.

Unter einem Nash-Gleichgewicht in reinen Strategien versteht man ein Strategieprofil 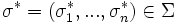$\sigma^* = (\sigma_1^*,...,\sigma_n^*) \in \Sigma$, bei dem die Strategie jedes Spielers i die beste Antwort auf die gewählten Strategien der anderen Spieler ist.

Unter der Voraussetzung, dass alle anderen Spieler an ihren gewählten Strategien festhalten, gibt es für Spieler i also kein 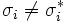$\sigma_i \neq \sigma_i^*$, das dem Spieler i eine höhere Auszahlung verspricht:

$\forall \sigma_i \in \Sigma_i: u_i(\sigma_1^*,\ldots,\sigma_i^*,\ldots, \sigma_n^*) \geq u_i(\sigma_1^*,\ldots,\sigma_i,\ldots, \sigma_n^*)$.

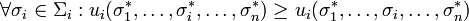Man sagt auch, dass Spieler i seine Auszahlung durch ein einseitiges Abweichen nicht verbessern kann. Ein Nash-Gleichgewicht zeichnet sich damit dadurch aus, dass sich kein Spieler durch eine einseitige Änderung seiner Strategie verbessern kann.

Gemischte Strategien

In manchen Fällen lässt man zu, dass die Spieler sich nicht auf eine bestimmte Strategie festlegen, sondern auf eine Wahrscheinlichkeitsverteilung, mit der die σ_i aus Σ_i zufällig gezogen werden. Ist Σ_i endlich oder zumindest abzählbar, so kann die Wahrscheinlichkeitsverteilung durch einen Vektor s_i beschrieben werden, wobei s_i,j die Wahrscheinlichkeit ist, dass die Strategie 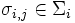$\sigma_{i,j} \in \Sigma_i$ gewählt wird.

Nash-Gleichgewicht

Die gemischte Strategie 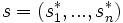$s = (s_1^*,...,s_n^*)$ ist genau dann ein Nash-Gleichgewicht, wenn kein Spieler durch alleiniges Abweichen eine bessere Auszahlung erreichen kann, das heißt genau dann, wenn

$\forall i \in 1..n \;\;\forall s_i \in S_i\;\;u_i(s_1^*,\ldots,s_{i-1}^*,s_i,s_{i+1}^*,\ldots, s_n^*) \leq u_i(s_1^*,\ldots,,s_{i-1}^*,s_i^*,s_{i+1}^*,\ldots, s_n^*)\$.

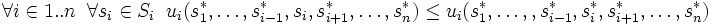Existenz eines Nash-Gleichgewichtes

Mit Hilfe des Fixpunktsatzes von Kakutani kann man zeigen, dass mindestens ein Nash-Gleichgewicht existieren muss, wenn folgende Voraussetzungen erfüllt sind:

1. Die Auszahlungsfunktionen 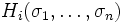$H_i(\sigma_1,\ldots,\sigma_n)$ sind stetig und quasikonkav in σ_i .
2. Die Strategiemengen $\Sigma_1,\ldots,\Sigma_n$ sind konvex und kompakt.

Häufig werden Spiele so konstruiert, dass die Σ_i endlich sind, endliche Mengen können jedoch nicht konvex sein. Allerdings ist die Menge der gemischten Strategien S_i über Σ_i kompakt und konvex und die entsprechende Erweiterung von H multilinear. Während die Existenz eines Nash-Gleichgewichtes in reinen Strategien also nicht garantiert werden kann, existiert mindestens ein Nash-Gleichgewicht bei einem Spiel in gemischten Strategien.

Ein einfacher Algorithmus zur Identifizierung von Nash-Gleichgewichten

Liegt ein Spiel in strategischer Form vor, so lassen sich alle Nash-Gleichgewichte in reinen Strategien durch folgenden Algorithmus bestimmen:

1. Optimiere die Entscheidung von Spieler i=1,...,n bei (beliebig) fixierten Strategien aller anderen Spieler: Markiere die unter diesen Umständen erreichbaren höchsten Auszahlungen für Spieler i. Wiederhole dies für alle möglichen Strategiekombinationen der anderen Spieler.
2. Führe 1. für alle Spieler durch.

Dann sind genau die Strategienkombinationen Nash-Gleichgewichte, bei denen alle Auszahlungen markiert sind. Diese Vorgehensweise eignet sich nur für eine geringe Anzahl von Spielern und Strategien.

Beispiel

Sei folgendes Spiel in Normalform gegeben:

		Spieler 2
		links	mitte	rechts
Spieler 1	oben	4 , 2	1 , 1	2 , 0
	mitte	2, 3	1 , 1	1, 4
	unten	3, 0	0, 2	1, 3

Dann funktioniert der Algorithmus wie folgt:

• i = 1:
  • gegeben Spieler 2 spielt Rechts: Für Spieler 1 ist oben optimal – markiere die 2 ("Oben ist beste Antwort auf Rechts")
  • gegeben Spieler 2 spielt Mitte: oben und mitte ist optimal – markiere die beiden 1en
  • gegeben Spieler 2 spielt Links: oben ist optimal – markiere die 4

• i = 2:
  • gegeben Spieler 1 spielt oben: Für Spieler 2 ist Links optimal – markiere die 2
  • gegeben Spieler 1 spielt mitte: Rechts ist optimal – markiere die 4
  • gegeben Spieler 1 spielt unten: Rechts ist optimal – markiere die 3

Das einzige Nash-Gleichgewicht ist also die Strategie, die zur Auszahlung 4, 2 führt: (oben,links).

Falls zu überprüfen ist, ob ein Tupel von gemischten Strategien ein Nash-Gleichgewicht ist, funktioniert obiger Algorithmus nur bedingt, da eine unendliche Anzahl an gemischten Strategien überprüft werden müsste.

Mit dieser Methode lassen sich übrigens auch strikt dominierte Strategien identifizieren: das sind genau die, bei denen keine Auszahlung markiert wurde.

Ein Algorithmus zur Identifizierung von Nash-Gleichgewichten in gemischten Strategien

Bei der Identifizierung von Nash-Gleichgewichten in gemischten Strategien ist es hilfreich, diejenigen gemischten Strategien zu identifizieren, die den Gegenspieler indifferent zwischen seinen Handlungsalternativen machen. Ist solch eine Strategie gefunden, sind alle Handlungen des Gegners beste Antworten. Treffen solche gemischten Strategien aufeinander, so sind sie folglich wechselseitig beste Antworten, es besteht kein Grund zum einseitigen Abweichen, und die gemischten Strategien bilden ein Nash-Gleichgewicht.

Beispiel

Sei der Kampf der Geschlechter mit folgenden Auszahlungen versehen:

		Spieler 2
		Oper	Fußball
Spieler 1	Oper	2, 5	0, 0
	Fußball	0, 0	5, 2

Dann funktioniert der Algorithmus wie folgt:

Spielt Spieler 2 mit einer Wahrscheinlichkeit von q Oper und mit der Gegenwahrscheinlichkeit von (1-q) Fußball, so ergeben sich für Spieler 1 folgende Erwartungsnutzen:

• EU1(O) = 2q
• EU1(F) = 5-5q

Spieler 1 ist also indifferent zwischen seinen beiden Strategien, wenn

• 2q = 5-5q, also wenn:
• 7q = 5 und somit:
• q = 5/7 gilt.

Für Spieler 2 lässt sich analog ermitteln, dass er indifferent ist, wenn Spieler 1 mit einer Wahrscheinlichkeit von p=2/7 Oper und mit (1-p)=5/7 Fußball spielt.

Da auf diese beiden Strategien alle Antworten des Gegenspielers beste Antworten sind, sind sie speziell jeweils auch wechselseitig beste Antworten. Somit kann [(2/7;5/7),(5/7;2/7)] als Nash-Gleichgewicht in gemischten Strategien identifiziert werden.

Spezialfälle

Ein Spezialfall von Nashs Existenzsatz für Gleichgewichte ist das für Zwei-Personen-Nullsummenspiele gültige Min-Max-Theorem, das 1928 durch John von Neumann bewiesen wurde. Anders als im allgemeinen Fall entspricht dabei jedem Spiel ein eindeutiger Auszahlungsvektor (v, − v), wobei v der Wert des Spieles heißt.

Für Zwei-Personen-Nullsummenspiele mit perfekter Information, zu denen Brettspiele wie Schach und Mühle gehören, existiert sogar immer ein Minimax-Gleichgewicht in reinen Strategien, das mit dem Minimax-Algorithmus rekursiv bestimmt werden kann. Dieser Satz wurde bereits 1912 von Ernst Zermelo bewiesen.

Praxisbeispiele

Marktwirtschaft

In der Marktwirtschaft ist eine Situation denkbar, bei der mehrere Anbieter in einem Markt die Preise ihrer konkurrierenden Produkte so weit gesenkt haben, dass sie gerade noch wirtschaftlich arbeiten. Für den einzelnen Anbieter wäre eine ausweichende Strategie nicht möglich: Senkt er seinen Preis, um seinen Absatz zu erhöhen, fällt er unter die Wirtschaftlichkeit; erhöht er ihn, werden die Käufer auf die Konkurrenzprodukte ausweichen und sein Gewinn sinkt ebenfalls. Ein Ausweg kann nun etwa darin bestehen, (beinahe) gleichzeitig mit einem Konkurrenten eine Produktinnovation einzuführen, um damit einen höheren Preis zu begründen. Unter dem Begriff Coopetition wurden derartige Szenarien Mitte der 1990er breiter diskutiert, wobei vor allem die Auseinandersetzung zwischen den US-amerikanischen Fluglinien als markantes Beispiel zitiert wurde.

Gefangenendilemma

Ein weiteres Beispiel ist das Gefangenendilemma, ein spieltheoretisches Problem, bei dem immer genau ein Nash-Gleichgewicht existiert.

Hierzu stelle man sich folgende Situation vor: Zwei Gefangene werden verdächtigt, gemeinsam eine Straftat begangen zu haben. Die Höchststrafe für das Verbrechen beträgt fünf Jahre. Beiden Gefangenen wird nun ein Handel angeboten, worüber auch beide informiert sind. Wenn einer gesteht und somit seinen Partner mitbelastet, kommt er ohne Strafe davon – der andere muss die vollen fünf Jahre absitzen. Entscheiden sich beide zu schweigen, bleiben nur Indizienbeweise, die aber ausreichen, um beide für zwei Jahre einzusperren. Gestehen aber beide die Tat, erwartet jeden eine Gefängnisstrafe von vier Jahren. Nun werden die Gefangenen unabhängig voneinander befragt. Weder vor noch während der Befragung haben die beiden die Möglichkeit, sich untereinander abzusprechen.

Für jeden der Gefangenen ist es optimal, zu gestehen, unabhängig davon, was der andere macht. Es existiert also ein Nash-Gleichgewicht.

Einzelnachweise

1. ↑ John Forbes Nash: Non-cooperative games, Dissertation, Princeton University 1950 (Online-Version)

Weblinks

• Game theory and Nash - Herleitung und Beispiele (engl.)
• Minimax-Strategie in der Praxis: Einfaches Zwei-Personen-Bluffspiel gegen den Computer