Nested Sets

Der Begriff Nested Sets (verschachtelte Mengen) bezeichnet ein Modell zur Abbildung eines Baumes mit Hilfe von Mengen, die ineinander verschachtelt sind. Dabei wird die "ist-Kind-von"-Beziehung auf eine "ist-Teilmenge-von"-Beziehung abgebildet. Das Modell wurde ursprünglich im Buch SQL for Smarties von Joe Celko vorgestellt. Es wird hauptsächlich im Rahmen von Datenbankanwendungen eingesetzt.

Klassische Baumstruktur

Der klassische Ansatz zur Implementierung einer Baumstruktur in einer Datenbank ist das Adjazenzlisten-Modell. Hierbei wird zu jedem Knoten eine Referenz auf dessen Elternknoten abgelegt. Die Wurzel hat dabei keinen Verweis zu einem Elternknoten (das Feld ist mit NULL belegt); ein Blatt ist ein Knoten, zu dem kein anderer Knoten verweist.

Baumstruktur als verschachtelte Mengen

Beim Nested-Sets-Modell wird die Baumstruktur in ineinander verschachtelte Mengen transformiert. Jeder Knoten entspricht einer Teilmenge; jede Teilmenge ist eine Teilmenge aller ihrer Eltern-Mengen.

In einer Datenbank können diese verschachtelten Mengen repräsentiert werden, indem für jede Teilmenge zwei Werte bestimmt werden, die die Grenzen dieser Teilmenge bestimmen. Diese Werte werden oft mit links und rechts bezeichnet. Der Wert links ist immer kleiner als rechts. Beide Werte einer Teilmenge sind größer als der Wert links ihrer Elternmenge und kleiner als deren Wert rechts.

Beispiel

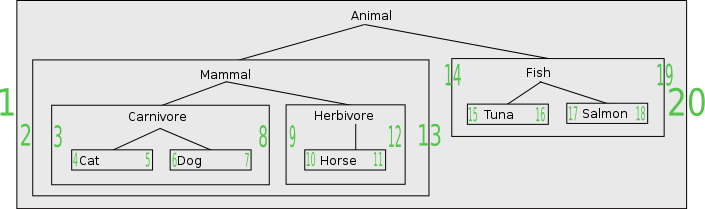
Die Grafik zeigt einen Baum, der in verschachtelte Mengen transformiert wurde. Die grünen Zahlen an den Rändern einer Menge sind die oben beschriebenen Werte links an der linken Kante und rechts an der rechten Kante.

Operationen

Knoten einfügen

Die Teilmenge für den ersten Knoten erhält die Werte 1 für links und 2 für rechts. Wird eine weitere Teilmenge für einen neuen Knoten unterhalb eines bestehenden Knotens eingefügt, wird rechts für die frischgebackene Elternmenge um 2 erhöht. Damit dies möglich ist, muss vorher im gesamten Baum jeder Wert links oder rechts, der größer als der ursprüngliche Wert rechts der neuen Elternmenge ist, ebenfalls um 2 erhöht werden. Die Werte rechts minus 2 und rechts minus 1 der Elternmenge werden dann der neu eingefügten Teilmenge als links und rechts zugeordnet.

Zu beachten ist hierbei, dass, anders als beim herkömmlichen Adjazenzlisten-Modell, die Reihenfolge der Kinder eines Knoten erhalten bleibt. Die soeben beschriebe Vorgehensweise ist äquivalent dazu, neue Knoten immer ans Ende der Liste der Kinder des Elternknotens anzuhängen. Genauso ist es denkbar, eine neue Teilmenge an beliebiger Stelle zwischen den anderen Teilmengen der Elternmenge einzufügen. Dabei müssen dann die Werte links und rechts der auf die neu eingefügte Teilmenge folgenden Kinder ebenfalls erhöht werden.

Transformieren einer Baumstruktur in verschachtelte Mengen

Eine bereits existierende Baumstruktur kann in verschachtelte Mengen überführt werden, in dem sie der Tiefe nach durchlaufen wird. Dabei werden, beginnend bei 1, die Kanten gezählt. Jedes mal, wenn ein Knoten betreten wird, wird diesem der Wert des Zählers als links zugeordnet und der Zähler erhöht. Wenn der Knoten verlassen wird, nachdem alle seine Kinder bearbeitet wurden, wird ihm der Wert des Zählers als rechts zugeordnet und der Zähler abermals erhöht.

Teilbaum entfernen

Um einen vollständigen Teilbaum zu entfernen, werden zunächst die Werte links und rechts der Wurzel des Teilbaumes bestimmt. Danach kann dieser entfernt werden, indem alle Teilmengen gelöscht werden, deren links und rechts innerhalb dieser Werte liegen. Abschließend müssen noch alle Werte links und rechts im übrigen Baum bei Knoten mit höheren Werten für links und rechts um die Breite des Teilbaumes verringert werden; die Breite ist hierbei die Differenz zwischen rechts und links dessen Wurzel plus 1.

Auswertung

Anzahl aller Knoten eines Teilbaums

Die Hälfte der Breite eines Teilbaums entspricht der Anzahl der Knoten in diesem Teilbaum inklusive der Wurzel. Somit kann die Anzahl der Knoten im gesamten Baum ermittelt werden, indem der Wert rechts minus dem Wert links der Wurzel durch zwei geteilt und (ab-)gerundet wird.

Pfad zu einem Knoten

Im Gegensatz zum Adjazenzlistenmodell muss beim Nested-Sets-Modell der Pfad zu einem Knoten nicht rekursiv ermittelt werden. Es genügt, alle Teilmengen zu selektieren, deren links-Werte kleiner sind und deren rechts-Werte gleichzeitig größer sind als die des betrachteten Knotens. Werden diese Teilmengen nach ihrem links-Wert sortiert, entspricht ihre Reihenfolge dem Weg von der Wurzel zum betrachteten Knoten.

Alle Knoten eines Teilbaumes

Alle Knoten unterhalb eines gegebenen Knotens können ermittelt werden, indem alle Teilmengen selektiert werden, deren Werte links und rechts sich innerhalb der Werte links und rechts des bearbeiteten Knotens befinden. Beim Adjanzenzlistenmodell müsste hier ebenfalls rekursiv vorgegangen werden.

Alle Blätter eines Teilbaumes

Die Abfrage nach einem kompletten Teilbaum kann leicht so modifiziert werden, dass nur Blätter, also Knoten ohne eigene Kinder, selektiert werden. Hierzu wird bei der Selektion als zusätzliches Kriterium rechts = links + 1 verwendet.

Tiefensuche

Mit Hilfe eines Self-Joins kann der Baum der Tiefe nach durchlaufen werden. Hierbei werden alle Tupel aus zwei Knoten selektiert, bei denen die Werte links und rechts des ersten Knotens zwischen den Werten links und rechts des zweiten Knotens liegt. Dabei kann die Tiefe jedes Knotens ermittelt werden, in dem gezählt wird, wie oft ein Tupel mit diesem Knoten als erstem Knoten auftritt. Das Ergebnis wird nach dem Wert links der enthaltenen Knoten sortiert.

Diese Abfrage könnte in SQL beispielsweise so aussehen:

 SELECT (COUNT(parent.id)-1) AS depth, node.id
 FROM tree AS node, tree AS parent
 WHERE node.l BETWEEN parent.l AND parent.r
 GROUP BY node.id ORDER BY node.l;

Vor- und Nachteile

• Die Komplexität beim Lesen ist in den meisten Fällen konstant. Beim Adjazenzlistenmodell ist der Aufwand linear abhängig von der Tiefe des bearbeiteten Knotens. Im Tausch ist eine Änderung des Baumes beim Nested-Sets-Modell wesentlich aufwändiger als beim Adjanzenzlistenmodell. Somit eignet es sich besser für Strukturen, die nicht häufig modifiziert, aber sehr oft gelesen werden.
• Die Darstellung als Mengen passt besser in die mengenorientierte Welt der Datenbanken. Mit der Abfragesprache SQL kann auf Mengen besser operiert werden als auf hierarchischen Strukturen.
• Das Abfragen der direkten Kinder eines Knotens ist schwierig.
• Die Reihenfolge der Kinder eines Knotens bleibt erhalten.

Weblinks

• Jede Menge Bäume - Nested Sets von Arne Klempert
• Bäume in SQL von Kristian Köhntopp
• Bäume in SQL von Christoph Reeg
• Workshop zum Thema Nested stets von Dipl.-Ing. (FH) Hartmut Kästner
• PHP PEAR Implementierung für Nested Sets - von Daniel Khan
• Nested Sets mit Doctrine ORM for PHP