Neubauer-Zählkammer

Neubauer improved-Zählkammer mit aufgelegtem Deckglas

Die Neubauer-Zählkammer ist eine etwa 30 mm x 80 mm große und etwa 5 mm dicke Glasplatte mit einer um einen definierten Betrag vertieften Mittelfläche, auf der quadratische Felder definierter Größe eingeätzt sind. Sie wird zur Zählung aller Arten von Teilchen, besonders von Zellen (zum Beispiel Erythrozyten, Leukozyten) und Mikroorganismen in der Medizin und Biologie verwendet.

Prinzip

In der Mitte der Glasplatte befindet sich die Fläche mit dem je nach Kammertyp unterschiedlichen Liniennetz (Zählfläche). Oft bildet dieses Netz zwei getrennte Zählfelder. Ein dünnes, plangeschliffenes Glasplättchen (Deckglas) wird auf die seitlich daneben befindlichen Auflagen (zwei plangeschliffene Glasstege) gelegt, die um einen genau bekannten Betrag (normalerweise 0,1 mm, zur Zählung sehr kleiner Teilchen wie Bakterien 0,02 mm) gegenüber der Zählfläche erhöht sind. Dadurch wird ein Raum mit definierter Höhe geschaffen. Die auszuzählende Teilchensuspension wird bei aufgelegtem Deckglas seitlich aufpipettiert und saugt sich durch Kapillarkraft in diesen Zwischenraum. Die Teilchensuspension wird so in einer Schicht mit genau bekannter Dicke ausgebreitet. Nach Auszählung der auf den Zählfeldern liegenden Teilchen unter dem Lichtmikroskop mit Durchlicht lässt sich deren Anzahl je Volumeneinheit errechnen. Bei Zellen kann neben ihrer Anfärbung auch das mikroskopische Phasenkontrastverfahren zur besseren Darstellung verwendet werden.

Vorbereitung der Kammer

Die Kammer sollte vor Gebrauch möglichst frei von Staub, Fusseln und Zellen sein. Zum korrekten Aufsetzen des Deckglases schiebt man es mit etwas Druck (Vorsicht, Bruchgefahr!) im Querformat auf die beiden Trägerstege auf. Wenn das Deckglas auf den Trägerstegen korrekt aufsitzt, sind sog. Newtonsche Ringe zu sehen. Das bedeutet, die Höhe des Zwischenraums zwischen den Trägerstegen und dem Deckglas liegt in der Größenordnung der Lichtwellenlängen, ist also zu vernachlässigen. In diesem Zustand verrutscht das Deckglas beim Kippen der Zählkammer nicht.

Das Zählgitter

Aufbau des Zählfeldes bei der Neubauer improved

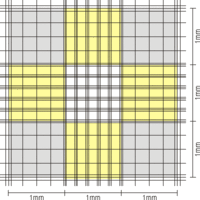
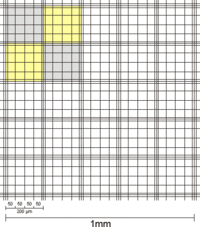
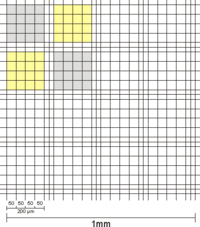
Das Zählgitter besteht bei der Neubauer-Zählkammer aus 3 x 3 Großquadraten von je 1 mm Kantenlänge und somit einer Fläche von je 1 mm². Das zentrale Großquadrat ist bei der Neubauer improved-Zählkammer wiederum in 5 x 5 kleinere Gruppenquadraten mit je 0,2 mm Kantenlänge unterteilt. Die Fläche eines solchen Gruppenquadrats ist damit 0,04 mm². Eine Besonderheit bei der Neubauer improved sind die dreifachen Begrenzungslinien der Gruppenquadrate, bei welchen die mittlere Linie die eigentliche Begrenzung zwischen zwei Feldern darstellt. Bei der alten Neubauer-Zählkammer (entspricht der Thoma-Zählkammer) ist das mittlere Großquadrat in 4 x 4 Gruppenquadrate von ebenfalls 0,2 mm Kantenlänge unterteilt. Diese sind auch durch dreifache Genzlinien getrennt, von denen aber nur jeweils die linke bzw. rechte als eigentliche Begrenzung anzusehen ist. Außerdem sind die Dreifachlinien nur an 2 Seiten zu finden.

Unterschied Mittleres Quadrat Neubauer alt und improved
(Mit gelb bzw. grau sind je zwei Gruppenquadrate markiert)
Neubauer improved	Neubauer- und Thoma-Zählkammer

Weiterhin ist jedes Gruppenquadrat in 4 x 4 Kleinstquadrate mit je 0,05 mm Kantenlänge mit je 0,0025 mm² Fläche eingeteilt.

Zählweise

CHO-Zellen im Phasenkontrast

Je nach Typ der auszuzählenden Zellen wird eine gewisse Anzahl Groß- oder Gruppenquadrate ausgezählt und daraus ein Mittelwert gebildet. Multipliziert man diesen Wert mit einem entsprechenden Faktor (Kehrwert des Produkts aus Quadratfläche und Kammerhöhe), erhält man die Zellzahl pro Volumeneinheit. Wichtig beim Zählen ist, dass man auf Grenzlinien liegende Zellen nicht doppelt zählt. Hierzu ist es üblich, bei der Auszählung eines Quadrates nur die Zellen auf zwei Grenzlinien (z. B. oben und links) mitzuzählen und die auf den anderen beiden Linien liegenden nicht. Vor der Auszählung ist es ratsam, das gesamte Linienraster mit einer geringen Vergrößerung zu betrachten und zu prüfen, ob die Zellen einigermaßen gleichmäßig über die Quadrate verteilt sind. Andernfalls sollte die Teilchensuspension nochmal aufgeschüttelt und neu aufgebracht werden. Eine ungleichmäße Verteilung erkennt man auch daran, dass sich bei der Auszählung mehrerer Quadrate stark schwankende Teilchenzahlen pro Quadrat ergeben.

Leukozytenzählung

Hierzu werden 4 große Eckquadrate ausgezählt und man teilt diese Anzahl durch 4, um einen Mittelwert pro Eckquadrat zu erhalten. Dieser Wert wird mit 10 multipliziert und man erhält damit die Anzahl der Zellen pro µl (Mikroliter). Der Faktor 10 errechnet sich dadurch, dass jedes Eckquadrat eine Fläche von 1 mm² hat und die Kammerhöhe 0,1 mm beträgt, also ein Eckquadrat einem Volumen von 0,1 µl = 0,1 mm³ = 0,1 mm x 1 mm² entspricht. Die Zellzahl pro Quadrat muss man jetzt durch das Volumen von 0,1 µl teilen oder einfach mit dessen Kehrwert 10 multiplizieren. Eine entsprechende Verdünnung, die man vor Aufbringen der Zellen auf die Kammer (zwangsläufig) gemacht hat, muss natürlich auch noch berücksichtigt werden.

Erythrozytenzählung

Um die Zahl kleinerer Zellen wie z. B. Erythrozyten oder CHO-Zellen in Zellkulturen zu bestimmen, werden viermal 5 Gruppenquadrate ausgezählt und so der Mittelwert für 5 Gruppenquadrate ermittelt. Diese Zahl mal 50 ergibt die Zellzahl pro µl (50 = 1 / (5 * 0,04 mm² x 0,1 mm). Auch hier ist eine eventuell zuvor gemachte Verdünnung zu berücksichtigen.

Reinigung

Nach Benutzung sollte man Kammer und Deckglas vorsichtig mit einem fusselfreien Einmaltuch von der Zellsuspension befreien und mit 70 % Ethanol oder einem ähnlichen Desinfektionsmittel reinigen und trocknen. Hierbei ist vor allem das Deckglas mit Vorsicht zu behandeln, da dieses plangeschliffen und daher um einiges teurer als ein normales Deckglas ist.

Andere Zählkammermodelle

• Bürker (9 Großquadrate mit je 1 mm Seitenlänge, unterteilt in je 4 x 4 kleine Quadrate mit Seitenlängen von 0,2 mm)
• Fuchs-Rosenthal (16 Großquadrate mit je 1 mm Seitenlänge und einer Kammerhöhe von 0,2 mm)
• Thoma (neu) (entspricht Neubauer improved ohne ausgeführte Eckquadrate und mit anderer Begrenzungsdarstellung)
• Schilling (Kreuznetz aus 3 x 3 Großquadraten, unterteilt in 4 x 4 Kleinstquadrate mit einer Fläche von je 0,0025 mm² und in 4 Rechtecke mit einer Fläche von 0,01 mm² und Einheitsnetz aus 9 Großquadraten, welche dem mittleren Quadrat des Kreuznetzes gleich sind)
• Türk (entspricht der alten Neubauer- bzw. Thoma-Kammer mit dem Unterschied, dass die Eckquadrate mit Doppellinien unterteilt sind)