Nichtpositive Zahl

Die reellen Zahlen ohne die Null (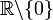$\mathbb{R} \backslash \{0\}$) werden in der Mathematik in positive und negative Zahlen unterschieden. Eine Zahl, die größer als null ist wie beispielsweise 3, nennt man positiv; ist sie kleiner als null wie z. B. −3 nennt man sie negativ. Positive Zahlen tragen ein Pluszeichen und negative Zahlen ein Minuszeichen als Vorzeichen. Das Pluszeichen wird normalerweise weggelassen.

Die gleiche Unterscheidung kann bei Teilmengen der reellen Zahlen vorgenommen werden, wie zum Beispiel bei den rationalen Zahlen oder den ganzen Zahlen.

Die negativen Zahlen sind bezüglich der Null am Zahlenstrahl symmetrisch zu den positiven Zahlen. Zahlen, die denselben Betrag (anschaulich: Auf der Zahlengerade den gleichen Abstand zur 0) besitzen, nennt man daher auch Gegenzahl. Die Gegenzahl einer positiven, rationalen Zahl x, ist das negative Gegenstück gleichen Betrags, also −x. Die Gegenzahl von −x ist wiederum x. 0 ist ihre eigene Gegenzahl.

In der mathematischen Literatur und speziell auch in der Informatik ist es teilweise auch gebräuchlich, die Null zu den positiven Zahlen hinzuzunehmen (in der Informatik wird teilweise auch zwischen −0, 0 und +0 unterschieden). Deshalb gibt es auch den einheitlich verwendeten Begriff der echt positiven Zahlen, bei denen die Null nicht hinzugerechnet wird.

In Bereichen der Physik kommt den positiven reellen Zahlen mit oder ohne Null eine besondere Bedeutung zu, da einige Zustandsgrößen keine negativen Werte und praktisch oft auch nicht den Wert 0 annehmen können. Beispiele sind die thermodynamische Temperatur, der Druck oder der elektrische Widerstand. Ist eine der Zustandsgrößen das Ergebnis einer quadratischen Gleichung oder einer Gleichung höherer Ordnung, so fallen nicht nur alle imaginären Lösungen der Gleichung, sondern auch alle negativ reellen Lösungen der Gleichung weg. Für die Menge der positiven reellen Zahlen wird das Symbol 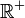$\mathbb{R}^+$ und für die Menge der positiven reellen Zahlen einschließlich 0 das Symbol 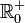$\mathbb{R}^+_0$ verwendet.

Unter den nichtnegativen Zahlen versteht man die positiven Zahlen und die Null zusammen. Analog versteht man unter den nichtpositiven Zahlen die negativen Zahlen und die Null zusammen. Die Null ist also weder positiv noch negativ, weshalb bisweilen ±0 oder, seltener, ∓0 geschrieben wird.

Da man bei einigen Zahlenmengen (z. B. komplexe Zahlen) keine mit der Addition und Multiplikation verträgliche Ordnung definieren kann, kann man für diese Zahlen auch nicht von größer oder kleiner als Null sprechen. Für die genauen Anforderungen an eine derartige Ordnungsrelation siehe geordneter Körper.

Eigenschaften

Die nichtnegativen ganzen Zahlen sind die natürlichen Zahlen (je nach Definition der natürlichen Zahlen muss man noch die Null entfernen). Hierbei hat sich die Schreibweise 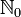$\mathbb{N}_0$ eingebürgert, wenn die Null in der Menge enthalten ist, ansonsten schreibt man $\mathbb{N}$. Die negativen ganzen Zahlen erhält man aus den ganzen Zahlen, indem man die natürlichen Zahlen und die Null entfernt.

Fasst man die positiven reellen (oder rationalen) Zahlen zur Menge P zusammen und die negativen reellen (oder rationalen) Zahlen zur Menge N, so ist die Vereinigung der Mengen P und N eine abelsche Gruppe bezüglich der Multiplikation.

Da z.B. die ganze Zahl 2 (bezüglich der Multiplikation) keine inverse ganze Zahl hat (1/2 ist keine ganze Zahl), gilt dies nicht für die ganzen Zahlen. Die Einheitengruppe {1; −1} des Rings der ganzen Zahlen ist zyklisch mit Länge 2. Anschaulich gesprochen bedeutet dies, dass man eine positive Zahl erhält, wenn man zwei negative oder zwei positive Zahlen miteinander multipliziert, jedoch eine negative, wenn man eine positive mit einer negativen Zahl multipliziert.

Siehe auch

• Signum