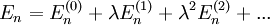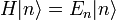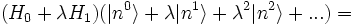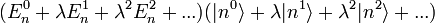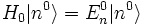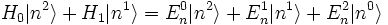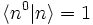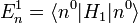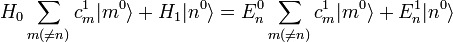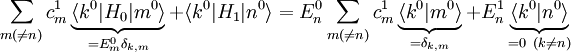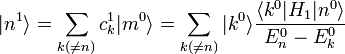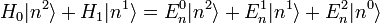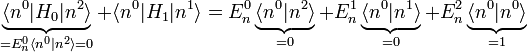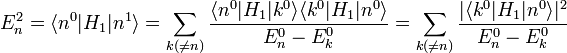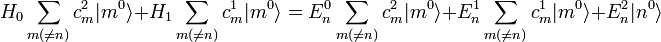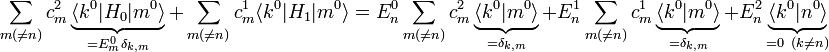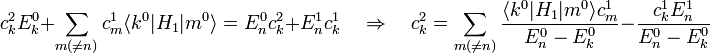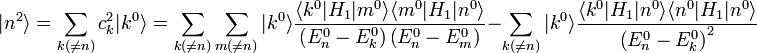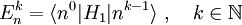- Nichtperturbativ
-
Die Störungstheorie ist eine wichtige Methode der theoretischen Physik, die Auswirkungen einer zeitunabhängigen Störung auf ein analytisch lösbares System untersucht. Vor der Erfindung des Computers war es nur durch solche Methoden möglich, Näherungslösungen für analytisch nicht geschlossen lösbare Probleme zu finden. Entwickelt wurde sie zunächst vor allem im Rahmen der Himmelsmechanik, bei der die Abweichungen der Planetenbahnen von der exakten Lösung des Zweikörperproblems, also den Ellipsen, durch Wechselwirkung mit anderen Himmelskörpern untersucht wurden. Im Folgenden geht es hauptsächlich um Anwendungen in der Quantenmechanik, während Anwendungen in der Himmelsmechanik im Artikel Störungsrechnung behandelt werden.
Die Störungstheorie ist als perturbativ anzusehen, da sie lediglich beliebig genaue Näherungen des unbekannten exakten Ergebnisses liefert und mit Potenzreihen arbeitet. Allerdings liefert die Methode der Störungstheorie nicht nur konvergente, reale Lösungen, sondern hauptsächlich asymptotische Reihen, die einer genauen Interpretation bedürfen.
Zeitabhängige Störungen werden im Artikel Fermis Goldene Regel behandelt.
Inhaltsverzeichnis
Stationäre Störungstheorie in der Quantenmechanik (Rayleigh-Schrödinger)
Die stationäre Störungstheorie kann bei Systemen angewendet werden, bei denen der Hamiltonoperator aus einem diagonalisierbaren Anteil und einer Störung besteht, die beide zeitunabhängig sind:
- H = H0 + λH1
Dabei soll der reelle Parameter λ so klein sein, dass die Störung das Spektrum von H0 nicht zu sehr verändert. Für die Konvergenz der Störungsreihe gibt es allerdings keine genauen Regeln; man muss sie im konkreten Fall explizit nachprüfen, zumal selbst bei infinitesimal-kleinem λ ein nach unten beschränkter Hamiltonoperator in einen unbeschränkten übergehen kann und selbst in scheinbar harmlosen Fällen, z. B. bei einer Störung λx4 mit positivem λ, Nichtkonvergenz deshalb auftritt, weil bei negativem λ ein unbeschränkter Operator entstehen würde.
Im Folgenden seien zum ungestörten Hamiltonoperator H0 die orthonormalen Eigenvektoren
 Eigenwerte
Eigenwerte 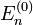 bekannt. Zusätzlich sollen die Eigenwerte des ungestörten Problems nicht entartet sein.
bekannt. Zusätzlich sollen die Eigenwerte des ungestörten Problems nicht entartet sein.Man setzt für die gestörten Eigenwerte und -zustände eine Potenzreihe im Parameter λ an, wir betrachten zunächst einen nicht entarteten Eigenraum zum Energieeigenwert En:
Hierbei versteht man unter den
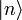 Abkürzungen für die Zustandsfunktionen
Abkürzungen für die Zustandsfunktionen 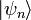 . Die oberen Indizes
. Die oberen Indizes 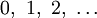 kennzeichnen bei den
kennzeichnen bei den 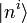 und den Ei die Ordnung der Störungstheorie und sollten nicht mit den entsprechenden Potenzen verwechselt werden, die bei den λi auftreten. Sie wurden deswegen in Klammern gesetzt.
und den Ei die Ordnung der Störungstheorie und sollten nicht mit den entsprechenden Potenzen verwechselt werden, die bei den λi auftreten. Sie wurden deswegen in Klammern gesetzt.Natürlich muss die zeitunabhängige Schrödingergleichung erfüllt sein:
Einsetzen der Potenzreihe liefert
Zusammenfassen von Gliedern gleicher Potenz in λ liefert die Folge von Gleichungen
usw.
Diese Gleichungen können iterativ nach
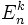 und
und 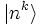 aufgelöst werden, der Term für k = 0 ist die ungestörte Schrödinger-Gleichung, man spricht daher auch von der Störung nullter Ordnung, wenn man sich auf die ursprüngliche, exakt bekannte Lösung bezieht, analog spricht man von der Störung k-ter Ordnung, wenn man die Lösung bis zu den Termen
aufgelöst werden, der Term für k = 0 ist die ungestörte Schrödinger-Gleichung, man spricht daher auch von der Störung nullter Ordnung, wenn man sich auf die ursprüngliche, exakt bekannte Lösung bezieht, analog spricht man von der Störung k-ter Ordnung, wenn man die Lösung bis zu den Termen 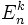 und
und 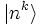 berechnet.
berechnet.Aus der zweiten Gleichung ist erkennbar, dass eindeutige Lösungen für
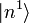 nur mit zusätzlichen Annahmen bestimmt werden können, da jede Linearkombination von
nur mit zusätzlichen Annahmen bestimmt werden können, da jede Linearkombination von 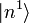 und
und 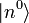 eine gültige Lösung ist. Eine geeignete zusätzliche Annahme zur eindeutigen Bestimmung der Störterme ist die Definition :
eine gültige Lösung ist. Eine geeignete zusätzliche Annahme zur eindeutigen Bestimmung der Störterme ist die Definition :Da der ungestörte Zustand
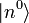 normiert sein soll, folgt sofort
normiert sein soll, folgt sofortund daraus (δik ist das Kronecker-Delta)
Man erhält in erster Ordnung die Korrekturen
und für die Korrektur der Energie in zweiter Ordnung
Herleitung der Korrekturen erster und zweiter Ordnung
Die Zustände
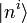 lassen sich nach den orthonormalen Eigenzuständen des ungestörten Problems
lassen sich nach den orthonormalen Eigenzuständen des ungestörten Problems 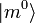 aufgrund deren Vollständigkeit entwickeln. Da
aufgrund deren Vollständigkeit entwickeln. Da 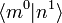 nach obiger Bedingung (
nach obiger Bedingung ( ) für m = n Null gibt, kann man bei der Summation über m das Glied m = n explizit ausschließen:
) für m = n Null gibt, kann man bei der Summation über m das Glied m = n explizit ausschließen:Energiekorrektur erster Ordnung
Die Gleichung erster Ordnung lautet:
Multipliziert man von links
 und nutzt dabei die Bra-Eigenwertgleichung
und nutzt dabei die Bra-Eigenwertgleichung 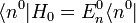 des ungestörten Hamiltonoperators sowie die Orthogonalität
des ungestörten Hamiltonoperators sowie die Orthogonalität 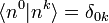 aus
auserhält man die Energiekorrektur erster Ordnung:
Zustandskorrektur erster Ordnung
Die Gleichung erster Ordnung mit entwickeltem
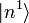 lautet:
lautet:Multipliziert man von links
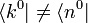
erhält man die Entwicklungskoeffizienten

und eingesetzt in obige Entwicklung nach den Eigenzuständen des ungestörten Problems die Zustandskorrektur erster Ordnung:
Energiekorrektur zweiter Ordnung
Die Gleichung zweiter Ordnung
Multipliziert man von links
 und nutzt dabei die Bra-Eigenwertgleichung
und nutzt dabei die Bra-Eigenwertgleichung 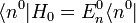 des ungestörten Hamiltonoperators sowie die Orthogonalität
des ungestörten Hamiltonoperators sowie die Orthogonalität 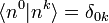 aus
auserhält man die Energiekorrektur zweiter Ordnung, wobei man
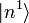 aus erster Ordnung einsetzt:
aus erster Ordnung einsetzt:Zustandskorrektur zweiter Ordnung
Die Gleichung zweiter Ordnung mit entwickeltem
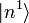 und
und  lautet:
lautet:Multipliziert man von links
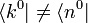
erhält man die Entwicklungskoeffizienten
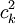 :
:Mit
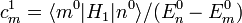 und
und 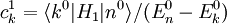 sowie
sowie  erhält man die Entwicklungskoeffizienten
erhält man die Entwicklungskoeffizienten 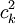
Die Zustandskorrektur zweiter Ordnung entwickelt nach den Eigenzuständen des ungestörten Problems:
Bemerkungen
Die Energiekorrektur k-ter Ordnung lässt sich allgemein angeben:
Zur Berechnung muss allerdings die Zustandskorrektur (k − 1)-ter Ordnung
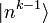 bekannt sein.
bekannt sein.Eine notwendige Bedingung für die Konvergenz einer störungstheoretischen Entwicklung ist, dass die Beiträge der Wellenfunktionen höherer Ordnung klein gegenüber denen niedrigerer Ordnung sind. Terme höherer Ordnung unterscheiden sich um Faktoren der Größenordnung
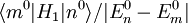 von denen niedrigerer Ordnung. Somit folgt die Bedingung:
von denen niedrigerer Ordnung. Somit folgt die Bedingung: für
für 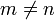
Im Allgemeinen ist diese Bedingung jedoch nicht hinreichend. Allerdings ist es bei divergierenden Reihen möglich, dass die Näherungen niedriger Ordnung die exakte Lösung gut approximieren (asymptotische Konvergenz).
An dem Ergebnis für
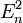 ist das Vorzeichen bemerkenswert: Bei Verschwinden der Effekte erster Ordnung wird die Grundzustandsenergie
ist das Vorzeichen bemerkenswert: Bei Verschwinden der Effekte erster Ordnung wird die Grundzustandsenergie 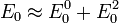 durch die Störung stets energetisch erniedrigt gegenüber
durch die Störung stets energetisch erniedrigt gegenüber 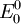 , und zwar durch Beimischung höherer angeregter Zustände (siehe
, und zwar durch Beimischung höherer angeregter Zustände (siehe 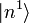 , Energie-Erniedrigung durch „Polarisation“).
, Energie-Erniedrigung durch „Polarisation“). da stets
da stets 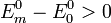
Störungstheorie mit Entartung
Die
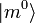 sind die Eigenfunktionen zum ungestörten Operator H0 mit den entsprechenden Eigenwerten
sind die Eigenfunktionen zum ungestörten Operator H0 mit den entsprechenden Eigenwerten 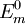 . Hier erkennt man auch das Problem bei der Behandlung von entarteten Zuständen in der Störungstheorie, da die Nenner verschwinden würden. Um dieses Problem zu lösen muss eine unitäre Transformation durchgeführt werden, um in den entarteten Eigenräumen H0 und H1 zu diagonalisieren. Danach treten die problematischen nichtdiagonalen Quadrate nicht mehr auf.
. Hier erkennt man auch das Problem bei der Behandlung von entarteten Zuständen in der Störungstheorie, da die Nenner verschwinden würden. Um dieses Problem zu lösen muss eine unitäre Transformation durchgeführt werden, um in den entarteten Eigenräumen H0 und H1 zu diagonalisieren. Danach treten die problematischen nichtdiagonalen Quadrate nicht mehr auf.Es liege jetzt ohne Störung Entartung vor (z. B.
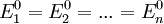 ). Dann erhält man die (nicht notwendig verschiedenen) Energiewerte
). Dann erhält man die (nicht notwendig verschiedenen) Energiewerte 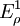 , für
, für 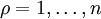 , und die zugehörigen Eigenvektoren
, und die zugehörigen Eigenvektoren 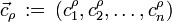 durch Diagonalisierung der hermitischen
durch Diagonalisierung der hermitischen 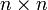 -Matrix
-Matrix 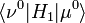 , für
, für 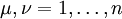 . Die auf diese Weise erhaltenen Zustandsvektoren
. Die auf diese Weise erhaltenen Zustandsvektoren  nennt man „die richtigen Linearkombinationen“ nullter Näherung (
nennt man „die richtigen Linearkombinationen“ nullter Näherung (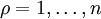 ).
).Geschichte
Die Störungstheorie wurde erstmals bei astronomischen Problemen verwendet und ist heute hauptsächlich in der Quantentheorie und der theoretischen Physik in Verwendung. Daneben wurde die Störungsstheorie in neuerer Zeit auch in den Wirtschaftswissenschaften zur Beschreibung mikroökonomischer Systeme verwandt, wobei die Entsprechung zu λ hier Perturbationskoeffizient heißt.
Anwendung
- Rabi-Formel in der Spektroskopie
Klassische Literatur
- Leonhard Eulers Werke zur Störungstheorie (Bände 26 und 27 der Series secunda)
- Martin Brendels Theorie der kleinen Planeten Teil I-IV (veröffentlicht 1898-1911)
Aktuelle Literatur
- Tosio Kato: Perturbation theory for linear operators, Springer, Berlin 1995, ISBN 3-540-58661-X
Siehe auch
- Fermis Goldene Regel (Zeitabhängige Störungstheorie)
- Störungsrechnung (Himmelsmechanik, Mathematik usw.)
Weblinks
Wikimedia Foundation.