- Noble Zahlen
-
Als noble Zahlen bezeichnet man solche irrationalen Zahlen, deren unendliche Kettenbruchdarstellung ab irgendeiner Stelle nur noch Einsen enthält.
Sie sind eng mit dem Goldenen Schnitt Φ verwandt und zeichnen sich dadurch aus, dass sie sich besonders schwer durch rationale Zahlen approximieren lassen.
Noble Zahlen sind algebraisch (vom Grad 2). Die Menge der noblen Zahlen ist folglich abzählbar.
Inhaltsverzeichnis
Φ als wichtigstes Element der noblen Zahlen
Die „nobelste“ Zahl
Der unendliche Kettenbruch für den Goldenen Schnitt ist:
Der Goldene Schnitt kann daher als die „nobelste“ Zahl bezeichnet werden – seine Kettenbruchdarstellung enthält von Anfang an ausschließlich Einsen.
Kettenbruchkonstruktion der noblen Zahlen
Die herausragende Stellung des Goldenen Schnittes innerhalb der noblen Zahlen wird anhand von Kettenbruchentwicklungen noch deutlicher.
Verallgemeinerte Kettenbrüche
Für endliche Kettenbruchentwicklungen rationaler Zahlen
d.h.
![q = [a_0;a_1,a_2,\cdots,a_{n-1},a_{n}]](/pictures/dewiki/49/15f676b9af6adbd2e2b903a2b13b4b4f.png) ,
,
gibt es zwei Formen, abhängig vom gewählten Abbruchkriterium. Einerseits kann man die Entwicklung beenden, sobald im Nenner eine ganze Zahl steht. Dadurch ergibt sich die kürzere Form, wobei
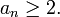 Führt man andererseits die Entwicklung fort, bis keine weitere Zerlegung in eine positive ganze Zahl und einen nicht verschwindenden Bruch möglich ist, so wird - einen Schritt später - zwangsläufig an + 1 = 1. Um Kettenbruchentwicklungen eindeutig zu definieren, wird für nicht ganzzahlige q (also für
Führt man andererseits die Entwicklung fort, bis keine weitere Zerlegung in eine positive ganze Zahl und einen nicht verschwindenden Bruch möglich ist, so wird - einen Schritt später - zwangsläufig an + 1 = 1. Um Kettenbruchentwicklungen eindeutig zu definieren, wird für nicht ganzzahlige q (also für 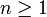 ) per Konvention
) per Konvention 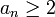 verlangt.
verlangt.Sofern der endliche Kettenbruch selbstverständlich eine rationale Zahl darstellt, spricht gegen die ungekürzte Form auch die Redundanz der letzten Eins:
beziehungsweise
In der gekürzten Form ist sie bereits im vorherigen (und als letztes aufgeführten) Glied enthalten.
Die explizite Angabe der am Ende stehenden Eins erlaubt jedoch, endliche Kettenbrüche auf einfache Weise über die rationalen Zahlen hinaus zu verallgemeinern, indem sie durch einen geeigneten Term ersetzt wird. Das zweite Semikolon erinnert daran, dass dieser Term nicht den Bedingungen genügen muss, denen a0 bis an unterliegen.
Es gilt:
![[a_0;a_1,\cdots,a_{n}]=[a_0;a_1,\cdots,a_{n};\infty]=[a_0;a_1,\cdots,\tilde a_{n};1] \mbox{ mit } \tilde a_{n}=a_{n}-1](/pictures/dewiki/97/a9a4bbbac28de7f53d8ac90fbe28cdae.png) .
.
Konstruktion
In zur Zerlegung umgekehrter Richtung lässt sich, beginnend von Eins, durch wiederholtes Reziprozieren und Addieren einer ganzen Zahl eine beliebige rationale Zahl konstruieren. So wie bezüglich dieser Kettenbruchkonstruktion 1 (oder alternativ
 ) als erzeugendes Element der rationalen Zahlen erachtet werden kann, ist Φ (wie auch
) als erzeugendes Element der rationalen Zahlen erachtet werden kann, ist Φ (wie auch 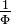 ) erzeugendes Element der noblen Zahlen. Analog zur endlichen Kettenbruchentwicklung rationaler Zahlen ist jede noble Zahl in der Form
) erzeugendes Element der noblen Zahlen. Analog zur endlichen Kettenbruchentwicklung rationaler Zahlen ist jede noble Zahl in der Formbeziehungsweise
![r = [a_0;a_1,a_2,\cdots,a_{n};\Phi]](/pictures/dewiki/101/e691468f0b2fdac5587cf8c9c59bc8cd.png) ,
,
darstellbar. Verlangt man dabei für
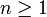 wieder
wieder 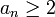 , so ist diese Darstellung als endlicher Kettenbruch über Φ ebenfalls eineindeutig.
, so ist diese Darstellung als endlicher Kettenbruch über Φ ebenfalls eineindeutig.Ähnlich der oben für rationale Werte angegebenen Identität gilt hier:
![[a_0;a_1,\cdots,a_{n},\bar 1]=[a_0;a_1,\cdots,a_{n};\Phi]=[a_0;a_1,\cdots,\tilde a_{n};\frac{1}{\Phi}] \mbox{ mit } \tilde a_{n}=a_{n}-1](/pictures/dewiki/102/fd27bc8f47171857dcfcc2ea87343a7b.png) .
.
Der erste dieser Kettenbrüche ist unendlich mit Periode 1, wie es der Definition nobler Zahlen entspricht.
Abzählbarkeit
Die Menge der noblen Zahlen ist eine Teilmenge der algebraischen Zahlen und daher abzählbar.
Ihre Abzählbarkeit ist auch anhand verallgemeinerter Kettenbruchentwicklungen leicht zu zeigen:
Die Abbildung
von
 auf die Menge der noblen Zahlen ist bijektiv.
auf die Menge der noblen Zahlen ist bijektiv.Beispiele
Sukzessive Kettenbruchkonstruktion einiger rationaler Zahlen sowie der korrespondierenden noblen Zahlen:
Fast noble Zahlen
Eine fast noble Zahl ist eine Zahl der Form
Siehe auch
Weblinks
- Eric W. Weisstein: Noble numbers und Near Noble Numbers auf MathWorld
Wikimedia Foundation.

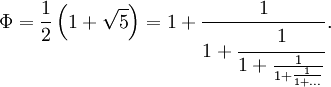
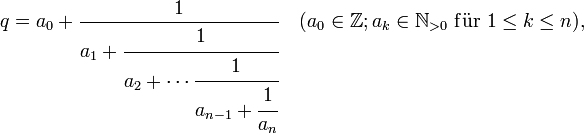
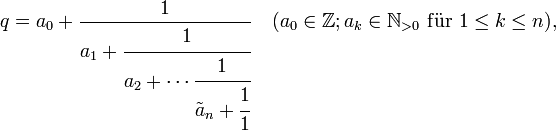
![q = [a_0;a_1,a_2,\cdots,\tilde a_{n};1]](/pictures/dewiki/55/7378ae1f95e932fb6ee5079bc4d6601c.png)
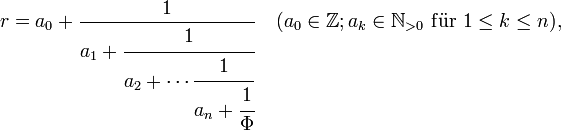
![[1] \rightarrow[\Phi]](/pictures/dewiki/54/60c01cfde877a8afa60b03ab777bc709.png)
![[a_0] \rightarrow[a_0;\Phi]\;\; (1\ne a_0\in\mathbb{Z})](/pictures/dewiki/53/5815cab62758ff665d7324700f19aedd.png)
![[a_0;a_1,\cdots,a_{n}] \rightarrow [a_0;a_1,\cdots,a_{n};\Phi]\quad(a_0\in \mathbb{Z}; a_k \in\mathbb{N}_{>0} \ \mathrm{f\ddot u r}\ 1\le k \le n; a_{n}\ne 1;n>0)](/pictures/dewiki/52/4a15835ef78dc057b9734619438922e7.png)

![[1,1,1,\ldots,1,n] =\frac1{1+\cfrac1{1+\cfrac1{1+\cfrac1{1+ \begin{matrix} {}&{} \\ \ddots & +\frac1n \end{matrix} }}}}](/pictures/dewiki/50/26a66105471a8fe046e6cdf03f8d6673.png)