Goldener Schnitt

Proportionen beim Goldenen Schnitt einer Strecke.

Beim Goldenen Schnitt (lateinisch: sectio aurea) oder auch bei der Goldenen Teilung – seltener beim Göttlichen Schnitt oder bei der Göttlichen Teilung (lateinisch: proportio divina) – entsteht ein bestimmtes Verhältnis zwischen zwei Zahlen oder zwei Größen.

Dieses Verhältnis ist die Goldene Zahl Φ (Phi) (oder das Goldene Verhältnis oder das Göttliche Verhältnis) und hat den Wert

$\Phi=\frac{1 + \sqrt{5}}{2} \approx 1{,}618$

Zum Beispiel stehen zwei Teile einer Strecke im Verhältnis Φ, wenn sich der größere zum kleineren Teil verhält wie die ganze Strecke zum größeren Teil.

Streckenverhältnisse wie beim Goldenen Schnitt werden seit der griechischen Antike als Inbegriff von Ästhetik und Harmonie angesehen. Sie werden als ideale Proportionen in Kunst und Architektur angewendet, kommen aber auch in der Natur vor. Das Goldene Verhältnis ist häufig bei der Bildkomposition in der Malerei zu finden und wird heute oft in der Photographie verwendet. Es zeichnet sich durch eine Reihe besonderer mathematischer Eigenschaften aus.

Umgangssprachlich wird Goldener Schnitt auch für die Goldene Zahl beziehungsweise für das Goldene Verhältnis gebraucht.

Definition und elementare Eigenschaften

Das Rechteck mit den Seiten a und b entspricht genau dann dem Goldenen Schnitt, wenn das auch für das Rechteck mit den Seiten a+b und a der Fall ist. Ein Goldenes Rechteck lässt sich daher stets in ein kleineres, ebenfalls Goldenes, und ein Quadrat zerlegen (animierte Darstellung).

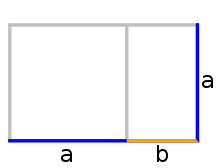
Zwei reelle Zahlen a > b > 0, zum Beispiel die Längen zweier Strecken, stehen genau dann im Verhältnis des Goldenen Schnitts, wenn die Gleichung

$\frac{a}{b}= \frac{a+b}{a}$

gilt. In Worten bedeutet dies, dass sich die größere zur kleineren verhält wie die Summe aus beiden zur größeren. Diese Eigenschaft ist ein Beispiel von Selbstähnlichkeit: Subtrahiert man die kürzere der beiden Strecken von der längeren, so erhält man eine noch kürzere Strecke a - b, zu der die mittlere Strecke b wiederum im Verhältnis des Goldenen Schnittes steht, also

$\frac{b}{a-b} = \frac{a}{b}$.

Die Goldene Zahl ist definiert als $\Phi:=\frac{a}{b}$. Sie hat den Wert

$\Phi = \frac{1 + \sqrt{5}}{2} \approx 1{,}618$     (siehe Herleitung des Zahlenwertes)

Die Goldene Zahl ist eine irrationale Zahl, das heißt sie lässt sich nicht als Bruch zweier ganzer Zahlen darstellen. Sie ist jedoch eine algebraische Zahl vom Grad 2, insbesondere kann sie mit Zirkel und Lineal konstruiert werden.

Geometrische Betrachtung

Konstruktionen mit Zirkel und Lineal

Als Konstruktionsverfahren betrachtet man in der Geometrie nur diejenigen Verfahren, die sich auf die Verwendung von Zirkel und Lineal (ohne Skala) beschränken. Für die Teilung einer Strecke im Verhältnis des Goldenen Schnittes gibt es eine Fülle derartiger Verfahren, von denen im Folgenden exemplarisch nur einige erwähnt werden. Man unterscheidet innere und äußere Teilung. Bei einer äußeren Teilung wird der in der Verlängerung der Ausgangsstrecke außen liegende Punkt gesucht. Die Ausgangsstrecke ist in diesem Fall die größere Teilstrecke. Aufgeführt sind auch zwei moderne, von Künstlern gefundene Konstruktionen.

Klassische innere Teilung

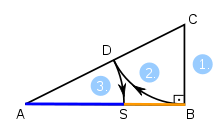
• Klassisches Verfahren mit innerer Teilung, das wegen seiner Einfachheit beliebt ist:

1. Errichte auf der Strecke AB im Punkt B eine Senkrechte der halben Länge von AB mit dem Endpunkt C.
2. Der Kreis um C mit dem Radius CB schneidet die Verbindung AC im Punkt D.
3. Der Kreis um A mit dem Radius AD teilt die Strecke AB im Verhältnis des Goldenen Schnittes.

Innere Teilung: Verfahren nach Euklid

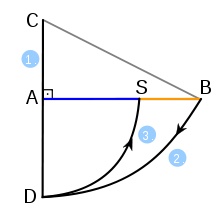
• Innere Teilung nach Euklid:

1. Errichte auf der Strecke AB im Punkt A eine Senkrechte der halben Länge von AB mit dem Endpunkt C.
2. Der Kreis um C mit dem Radius CB schneidet die Verlängerung von AC im Punkt D.
3. Der Kreis um A mit dem Radius AD teilt die Strecke AB im Verhältnis des Goldenen Schnittes.

Äußere Teilung

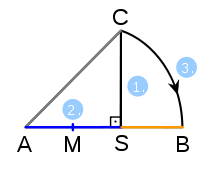
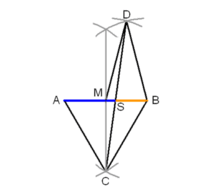
• Klassisches Verfahren mit äußerer Teilung:

1. Errichte auf der Strecke AS im Punkt S eine Senkrechte der Länge AS mit dem Endpunkt C.
2. Konstruiere die Mitte M der Strecke AS.
3. Der Kreis um M mit dem Radius MC schneidet die Verlängerung von AS im Punkt B. S teilt AB im Verhältnis des Goldenen Schnittes.

Konstruktion nach Odom

• Konstruktion nach dem amerikanischen Künstler George Odom, die dieser 1982 entdeckte:

1. Konstruiere ein gleichseitiges Dreieck.
2. Konstruiere den Umkreis, also den Kreis, der durch alle Ecken des Dreiecks verläuft.
3. Halbiere zwei Seiten des Dreiecks in den Punkten A und S.
4. Die Verlängerung von AS schneidet den Kreis im Punkt B. S teilt AB im Verhältnis des Goldenen Schnittes.

Beginnt man mit der Strecke AS, so konstruiert man über der halben Strecke das in S rechtwinklige Dreieck mit dem Umkreismittelpunkt (Höhe: AS/2, 2. Kathete: AS)

Konstruktion nach Hofstetter

• Konstruktion nach dem österreichischen Künstler Kurt Hofstetter, die dieser 2005 im Forum Geometricorum ^[1] publizierte:

1. Halbiere die Strecke AB in M durch Streckensymmetrale mit Radius AB und konstruiere dabei ein gleichseitiges Dreieck ABC mit der Seitenlänge AB und C unterhalb von AB.
2. Konstruiere ein gleichschenkeliges Dreieck MBD mit Schenkellänge AB über der Grundlinie MB
3. Die Strecke CD teilt die Strecke AB im Verhältnis des Goldenen Schnittes.

Anstatt immer neu zu konstruieren, wurde im 19. Jahrhundert von Künstlern und Handwerkern ein Goldener Zirkel – ein auf das Goldene Verhältnis eingestellter Reduktionszirkel – benutzt. Andere Instrumente hatten die Form eines Storchschnabels.

Pentagramm

Pentagramm

Faltet man einen Papierstreifen nach Art eines Überhandknotens, so entstehen Strecken im Verhältnis des Goldenen Schnittes.

Das Pentagramm, eines der ältesten magischen Symbole der Kulturgeschichte, steht in einer besonders engen Beziehung zum Goldenen Schnitt.

Zu jeder Strecke und Teilstrecke im Pentagramm findet sich ein Partner, der mit ihr im Verhältnis des Goldenen Schnitts steht. In der Abbildung sind alle drei möglichen Streckenpaare jeweils blau (längere Strecke) und orange (kürzere Strecke) markiert. Sie lassen sich über das oben beschriebene Verfahren der stetigen Teilung nacheinander erzeugen. Im Prinzip ist es in das verkleinerte Pentagramm fortsetzbar, das man in das innere Fünfeck zeichnen könnte, und damit auch in alle weiteren. Stünden die beiden Strecken in einem Verhältnis ganzer Zahlen, müsste dieses Verfahren der fortgesetzten Subtraktion irgendwann Null ergeben und damit abbrechen. Die Betrachtung des Pentagramms zeigt aber anschaulich, dass das nicht der Fall ist.

Für den Beweis, dass es sich um den Goldenen Schnitt handelt, beachte man, dass neben den vielen Strecken, die aus offensichtlichen Symmetriegründen gleich lang sind, auch CD=CC' gilt. Ursache ist, dass das Dreieck DCC’ zwei gleiche Winkel besitzt, wie man durch Parallelverschiebung der Strecke CC’ erkennen kann, und daher gleichschenklig ist. Nach dem Strahlensatz gilt:

$\frac{\ \overline\mathrm{AB}\ }{\ \overline\mathrm{BB'}\ } = \frac{\ \overline\mathrm{AC}\ }{\overline\mathrm{CC'}}$

Ersetzt man AC=AB+BC und beachtet die Gleichheit der auftretenden Teilstücke, so erhält man genau die obige Definitionsgleichung für den Goldenen Schnitt.

Goldenes Rechteck und Dreieck

Ein Rechteck, dessen Seitenverhältnis dem Goldenen Schnitt entspricht, bezeichnet man als Goldenes Rechteck. Ebenso nennt man ein gleichschenkliges Dreieck, bei dem zwei Seiten in diesem Verhältnis stehen Goldenes Dreieck.

• zum Vergleich von Rechtecksproportionen siehe Abschnitt Vergleich mit anderen Teilungsverhältnissen
• ein goldenes Dreieck ist Inhalt der Methode äußere Teilung in Abschnitt Konstruktionen mit Zirkel und Lineal

Goldener Winkel

Der Goldene Winkel $\Psi\approx 137{,}5^\circ$

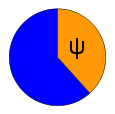
Den Goldenen Winkel Ψ erhält man, wenn man den Kreis mittels Winkel im Verhältnis des Goldenen Schnittes teilt. Bezeichnet man den kleineren dieser Winkel als Ψ₁ und den größeren als Ψ₂, so ergibt sich

$\Psi_2=\frac{360^\circ}{\Phi}\approx 222{,}5^\circ\,.$

Da sich Winkel kleiner als 180° für die Praxis als handlicher erweisen, wird gewöhnlich der kleinere Winkel Ψ₁ als Goldener Winkel Ψ bezeichnet, das heißt

$\Psi=360^\circ-\frac{360^\circ}{\Phi}\approx 137{,}5^\circ\,.$

Durch wiederholte Drehung um den Goldenen Winkel entstehen immer wieder neue Positionen, etwa für die Blattansätze in nebenstehendem Bild. Wie bei jeder irrationalen Zahl werden dabei nie exakte Überdeckungen entstehen. Durch die Drehung um den Goldenen Winkel wird erreicht, dass die Überdeckung der Blätter, welche die Photosynthese behindert, in der Summe minimiert wird.

Goldene Spirale

Goldene Spirale

Ein Goldenes Rechteck lässt sich in ein Quadrat und ein weiteres Goldenes Rechteck zerlegen. Durch wiederholte Teilung erhält man eine Figur, in die sich eine gewisse logarithmische Spirale einzeichnen lässt, die Goldene Spirale. Sie wird oft, wie in nebenstehender Abbildung, durch eine Folge von Viertelkreisen approximiert. Ihr Radius ändert sich bei jeder 90°-Drehung um den Faktor Φ.^{[* 1]}

r(φ) = ae^kφ mit der Steigung $k = \tfrac{\ln{\Phi}}{\alpha_\llcorner}$, wobei $\alpha_\llcorner$ hierbei der Zahlenwert für den rechten Winkel, also 90° oder anders ausgedrückt $\tfrac{\pi}{2}$ ist.

$|k| = 0{,}00535^\circ = 0{,}306\,\mathrm{rad}$

Die schneckenförmigen Kalkgehäuse einiger Tierarten haben eine ähnliche Steigung, wie beispielsweise das des Nautilus. Bei den meisten dieser Tierarten ist die Steigung jedoch eher geringer.

Goldener Schnitt im Ikosaeder

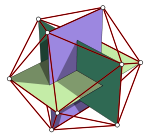Drei Goldene Rechtecke im Ikosaeder

Die zwölf Ecken des Ikosaeders bilden die Ecken von drei gleich großen, senkrecht aufeinanderstehenden Rechtecken mit gemeinsamem Mittelpunkt und mit den Seitenverhältnissen des Goldenen Schnittes. Die Anordnung der drei Rechtecke heißt auch Goldener-Schnitt-Stuhl.

Mathematische Eigenschaften

Herleitung des Zahlenwertes

Aus der oben angegebenen Definition

$\frac{a}{b} = \frac{a+b}{a} = 1 + \frac{b}{a}$

bzw.

$\frac{a}{b} - 1 - \frac{b}{a} = 0$

folgt mit

$\Phi = \frac{a}{b}$   und   ${1\over\Phi} = \frac{b}{a}$

$\Phi - 1 - {1\over\Phi} = 0$

Multiplizieren mit Φ ergibt die quadratische Gleichung

Φ² − Φ − 1 = 0

Diese Gleichung hat genau zwei algebraisch konjugierte Lösungen

$\Phi = \frac{1+\sqrt{5}}{2} \approx 1{,}618\,033$

und

$\bar\Phi = \frac{1-\sqrt{5}}{2} = 1 - \Phi = - {1\over\Phi} \approx -0{,}618\,033$

Da $\bar\Phi$ negativ ist, ist Φ die gesuchte Goldene Zahl.

Die Goldene Zahlenfolge

Goldene Zahlenfolge für a₀=1

z	$a_z=\Phi^z\cdot a_0$
4	≈ 6,854	Φ4 = 3 * Φ + 2
3	≈ 4,236	Φ3 = 2 * Φ + 1
2	≈ 2,618	Φ2 = Φ + 1
1	≈ 1,618	Φ
0	= 1,000	Φ0 = 1
−1	≈ 0,618	Φ − 1 = Φ − 1
−2	≈ 0,382	Φ − 2 = − Φ + 2
−3	≈ 0,236	Φ − 3 = 2 * Φ − 3
−4	≈ 0,146	Φ − 4 = − 3 * Φ + 5

Zu einer gegebenen Zahl a₀ lässt sich eine Folge $a_z:=\Phi^z\cdot a_0$ für $z\in\Z$ konstruieren. Diese Folge hat die Eigenschaft, dass je drei aufeinanderfolgende Glieder (a_{z − 1},a_z,a_{z + 1}) einen Goldenen Schnitt bilden, das heißt es gilt

$\frac{a_z}{a_{z-1}}=\frac{a_{z+1}}{a_z}\qquad\textrm{sowie}\qquad a_{z+1}=a_z+a_{z-1}\qquad\mathrm{f\ddot ur\,alle}\,z\in\Z\,.$

Diese Folge spielt in der Proportionslehre in Kunst und Architektur eine wichtige Rolle, weil sich zu einer gegebenen Länge a₀ weitere dazu harmonisch wirkende Längen erzeugen lassen. Dadurch lassen sich auch Objekte sehr unterschiedlicher Abmessungen, wie etwa Fenster- und Raumbreite, mittels des Goldenen Schnitts in Bezug setzen und ganze Serien untereinander harmonischer Maße erstellen.

Zusammenhang mit den Fibonacci-Zahlen

Verhältnisse aufeinanderfolgender
Fibonacci-Zahlen

fn	fn + 1	$\frac{f_{n+1}}{f_n}$	Abweichung zu Φ in %
1	1	= 1,0000	−38
1	2	= 2,0000	+23
2	3	= 1,5000	−7,3
3	5	≈ 1,6667	+3,0
5	8	= 1,6000	−1,1
8	13	= 1,6250	+0,43
13	21	≈ 1,6154	−0,16
21	34	≈ 1,6190	+0,063
34	55	≈ 1,6176	−0,024
55	89	≈ 1,6182	+0,0091
89	144	≈ 1,6180	−0,0036
144	233	≈ 1,6181	+0,0013

In einem engen Zusammenhang zum Goldenen Schnitt steht die unendliche Zahlenfolge der Fibonacci-Zahlen (siehe unten die Abschnitte Mittelalter und Renaissance):

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …

Die jeweils nächste Zahl in dieser Folge erhält man als Summe der beiden vorangehenden. Das Verhältnis zweier aufeinanderfolgender Zahlen der Fibonacci-Folge strebt gegen den Goldenen Schnitt (siehe Tabelle). Das rekursive Bildungsgesetz f_{n + 1} = f_n + f_{n − 1} bedeutet nämlich

$\frac{f_{n+1}}{f_n} = \frac{f_n+f_{n-1}}{f_n} = 1 + \frac{f_{n-1}}{f_n}.$

Sofern dieses Verhältnis gegen einen Grenzwert Φ konvergiert, muss für diesen gelten

$\Phi = 1 + \frac{1}{\Phi}.$

Diese Beziehung definiert aber gerade den Goldenen Schnitt, wie der Vergleich mit der ersten Gleichung des vorangehenden Abschnitts zeigt. Diese Argumentation gilt auch für verallgemeinerte Fibonacci-Folgen mit zwei beliebigen Anfangsgliedern.

Die Glieder der Fibonacci-Folge f_n lassen sich für alle $n \in \N$ über die Formel von Binet berechnen:

$f_n = \frac{1}{\sqrt{5}} (\Phi^n - \bar\Phi^n).$

Diese Formel liefert die richtigen Anfangswerte f₀ = 0 und f₁ = 1 und erfüllt die rekursive Gleichung f_{n + 1} = f_n + f_{n − 1} für alle n.

Approximationseigenschaften der Goldenen Zahl

Wie weiter oben schon angegeben, ist die Goldene Zahl Φ eine irrationale Zahl, das heißt sie lässt sich nicht als Bruch zweier ganzer Zahlen darstellen. Sie wird manchmal die „irrationalste“ aller Zahlen genannt, weil sie sich (in einem speziellen zahlentheoretischen Sinn) besonders schlecht durch rationale Zahlen approximieren lässt (Diophantische Approximation). Dies soll im Folgenden durch einen Vergleich mit der ebenfalls irrationalen Kreiszahl π illustriert werden. Letztere ist wesentlich besser approximierbar als Φ, zum Beispiel lässt π sich durch den Bruch $\tfrac{22}{7}$ mit einer Abweichung von nur zirka 0,00126 approximieren. Einen derartig geringen Fehler würde man im Allgemeinen erst bei einem sehr viel größeren Nenner erwarten.^[2]

Die Goldene Zahl lässt sich direkt aus der Forderung nach möglichst schlechter Approximierbarkeit durch rationale Zahlen konstruieren. Um das zu verstehen, betrachte man das folgende Verfahren zur Approximation beliebiger Zahlen durch einen Bruch am Beispiel der Zahl π. Wir zerlegen diese Zahl zunächst in ihren ganzzahligen Anteil und einen Rest, der kleiner als 1 ist: π = 3 + Rest. Der Kehrwert dieses Restes ist eine Zahl, die größer als 1 ist. Sie lässt sich daher wiederum zerlegen in einen ganzzahligen Anteil und einen Rest kleiner 1: $\pi = 3 + \tfrac{1}{7 + \text{Rest}}$. Verfährt man mit diesem Rest und allen folgenden ebenso, dann erhält man die so genannte unendliche Kettenbruchentwicklung der Zahl π

$\pi = 3 + \frac{1}{7 + \frac{1}{15 + \frac{1}{1 + \cdots}}}.$

Wenn man diese Kettenbruchentwicklung nach endlich vielen Schritten abbricht, dann erhält man für π die bekannten Näherungen 3, $\tfrac{22}{7}$, $\tfrac{333}{106}$, $\tfrac{355}{113}$, …, die rasch gegen π streben. Für jeden einzelnen dieser Brüche gilt, dass es keinen Bruch mit einem kleineren Nenner gibt, der π besser approximiert. Dies gilt ganz allgemein:

Wenn man die Kettenbruchentwicklung einer irrationalen Zahl x an irgendeiner Stelle abbricht, so erhält man eine rationale Zahl p / q, die x optimal approximiert unter allen rationalen Zahlen mit Nenner $\le q$.^[3]

Im obigen Kettenbruch erscheint vor jedem Pluszeichen eine ganze Zahl. Je größer diese Zahl ist, umso kleiner ist der Bruch, in dessen Nenner sie steht, und umso kleiner ist daher auch der Fehler, der entsteht, wenn der unendliche Kettenbruch vor diesem Bruch abgebrochen wird. Die größte Zahl im obigen Abschnitt des Kettenbruchs ist die 15. Das ist der Grund, warum $\tfrac{22}{7}$ eine derart gute Approximation für π darstellt.

In Umkehrung dieser Argumentation folgt nun, dass die Approximation besonders schlecht ist, wenn die Zahl vor dem Pluszeichen besonders klein ist. Die kleinste zulässige Zahl dort ist aber die 1. Der Kettenbruch, der ausschließlich Einsen enthält, lässt sich daher besonders schlecht durch rationale Zahlen approximieren und ist in diesem Sinn die „irrationalste aller Zahlen“.

Für die Goldene Zahl gilt nun aber $\Phi = 1 + \tfrac{1}{\Phi}$ (siehe oben), woraus sich durch wiederholte Anwendung ergibt

$\Phi = 1 + \frac{1}{\Phi} = 1 + \frac{1}{1 + \frac{1}{\Phi}} = \cdots = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{\cdots}{\cdots + \frac{1}{\Phi}}}}}.$

Da die Kettenbruchentwicklung der Goldenen Zahl Φ also nur Einsen enthält, gehört sie zu den Zahlen, die besonders schlecht rational approximierbar sind. Bricht man ihre Kettenbruchentwicklung an irgendeiner Stelle ab, so erhält man stets einen Bruch aus zwei aufeinanderfolgenden Fibonacci-Zahlen.

Eine weitere kuriose Bezeichnung ist die folgende: in der Theorie der dynamischen Systeme bezeichnet man Zahlen, deren unendliche Kettenbruchdarstellung ab irgendeiner Stelle nur noch Einsen enthält, als „noble Zahlen“. Da die Goldene Zahl nur Einsen in ihrem Kettenbruch hat, kann man sie scherzhaft als „nobelste Zahl“ bezeichnen.

Weitere mathematische Eigenschaften

• Aus Φ² = 1 + Φ lässt sich folgende unendliche Kettenwurzel herleiten:

$\Phi = \sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+\ldots}}}}$

• Das Quadrat Φ² = Φ + 1 und jede höhere ganzzahlige Potenz von Φ lassen sich als Summe aus einem ganzzahligen Vielfachen von Φ und einem ganzzahligen Vielfachen von 1 darstellen. Auf dieser Eigenschaft beruht die fundamentale Bedeutung des goldenen Schnitts für quasiperiodische Gitter (siehe Quasikristall).
• Genauer gilt $\Phi^n = \Phi^{n-1}+\Phi^{n-2} = f_{n-1} + f_n \cdot \Phi = f_{n+1} + f_n \cdot \tfrac{1}{\Phi}$ (wobei f_n die n-te Fibonacci-Zahl ist).
• In der Trigonometrie gilt unter anderem

$\Phi = 2\cos(\tfrac{\pi}{5})$

oder auch

$\sin(\tfrac{\pi}{10}) = \frac{\Phi-1}{2}$

$\sin(\tfrac{3 \pi}{10}) = \frac{\Phi}{2}$

Dabei lässt sich $\tfrac{\pi}{10}$ als die Hälfte des Winkels in der Spitze des Pentagramms interpretieren und $\tfrac{3\pi}{10}$ als die Hälfte des stumpfen Außenwinkels. Gelegentlich wird die Rolle des Goldenen Schnitts für das Fünfeck als vergleichbar bedeutend bezeichnet wie die der Kreiszahl π für den Kreis.

• Der goldene Schnitt lässt sich auch mit Hilfe der Eulerschen Zahl und der hyperbolischen Areasinus-Funktion ausdrücken:

$\Phi^{\pm1} = e^{\operatorname{arsinh}\left(\pm\tfrac{1}{2}\right)}$

• Das Einsetzen von $\tfrac{1}{\Phi}$ in die geometrische Reihe liefert den folgenden Zusammenhang:

$\Phi = \sum_{k=1}^\infty\frac{1}{\Phi^k}$

Geschichte

Antike

Die erste erhalten gebliebene genaue Beschreibung des Goldenen Schnittes stammt von Euklid (um 300 v. Chr.), der darauf über seine Untersuchungen an den platonischen Körpern und dem Fünfeck beziehungsweise dem Pentagramm stieß. Seine Bezeichnung für dieses Teilungsverhältnis wurde später als „proportio habens medium et duo extrema“ übersetzt, was heute als „Teilung im inneren und äußeren Verhältnis“ bezeichnet wird.^[4]

Mittelalter

Liber abbaci, MS Biblioteca Nazionale di Firenze, Codice Magliabechiano cs cI 2616, fol. 124r: Fibonacci-Zahlen am Rand der „Kaninchenaufgabe“

In seinem Rechenbuch Liber abbaci (nicht erhaltene Erstfassung 1202, erhaltene 2. Fassung nicht vor 1220), einem umfangreichen arithmetischen und algebraischen Lehrwerk über das Rechnen mit den indo-arabischen Ziffern, kommt der italienische Mathematiker Leonardo da Pisa, genannt „Fibonacci“, kurz auch auf die später nach ihm benanten Fibonacci-Folge zu sprechen, und zwar im Zusammenhang mit der sogenannten Kaninchen-Aufgabe, in der zu errechnen ist, wie viele Kaninchenpaare bei einer Fortpflanzungsrate von einem Paar Jungkaninchen pro Elternpaar und Monat nach Ablauf eines Jahres insgesamt vorhanden sind, wenn ein erstes Paar bereits im ersten Monat und dessen Nachwuchs jeweils ab seinem zweiten Lebensmonat Junge wirft.^[5] Leonardo führt die Zahlen für jeden Monat vor (2, 3, 5, 8 ... bis 377) und weist darauf hin, dass sich jedes Glied der Reihe (ab dem dritten) durch Summierung der beiden vorhergehenden Reihenglieder errechnen lässt. Eine weitere Beschäftigung mit dieser Folge findet sich bei ihm nicht. Dass ihm auch der Goldene Schnitt bekannt und in der Tradition Euklids ein Begriff war, zeigt sich gegen Ende seines Werks bei einer algebraischen Aufgabe, in der es darum geht (in moderner Formulierung wiedergegeben)^[6] a und b zu finden mit 10 = a + b und $\tfrac{a}{b} + \tfrac{b}{a} = \sqrt{5}$. Hierzu weist Leonardo darauf hin, dass im Fall von a > b die Proportion 10:a = a:b gilt, 10 also von a und b im Verhältnis des Goldenen Schnitts geteilt wird ("et scis, secundum hanc diuisionem, 10 diuisa esse media et extrema porportione; quia est sicut 10 ad maiorem partem, ita maior pars ad minorem").^[7]

Renaissance

Einen Zusammenhang zwischen Fibonacci-Folge und Goldenem Schnitt stellte Leonardo jedoch noch nicht her: Die Entdeckung, dass sich bei Teilung eines Gliedes der Fibonacci-Folge durch das vorhergehende Reihenglied als Näherungswert Φ ergibt, wurde lange Zeit Johannes Kepler zugeschrieben, konnte jedoch in jüngerer Zeit auch schon in einer handschriftlichen Anmerkung nachgewiesen werden, mit der ein mutmaßlich aus Italien stammender Leser in der ersten Hälfte des 16. Jahrhunderts Euklids Theorem II.11 in der Euklid-Ausgabe Paciolis von 1509 kommentierte:^[8]

Sit linea ab 233 pedum, divisa ut docet 11 huius in duo inaequalia in puncto h et sit bh portio eius maior 144 et ha portio eius minor 89. ducatur ab in ha et perveniunt 20737 et bh in se et perveniunt 20736. et sic cognosces quod in mutationibus non est laborandum quid impossibile est numerum ita dividi ut ista 11 proponit. similiter accidit si linea 13 pedum dividatur in lineam 8 pedum, et lineam 5. ["Eine Gerade ab von 233 Fuß sei so, so wie es Theorem 11 hier vorführt, an einem Punkt h in zwei ungleiche Teile geteilt, und dabei sei bh sein größerer Teil mit 144 und ha sein kleinerer Teil mit 89. ab sei multipliziert mit ha, und es ergeben sich 20737, und bh multipliziert mit sich selbst, so ergeben sich 20736. Und daran magst du erkennen, dass man sich nicht mit Ersetzungen abzumühen braucht um zu zeigen, dass es unmöglich ist, die Zahl so zu teilen wie es hier Theorem 11 vorführt. Das gleiche ergibt sich, wenn eine Gerade von 13 Fuß in eine Gerade von 8 und eine von 5 Fuß geteilt wird."]

Der vitruvianische Mensch, Leonardo da Vinci, 1492, Proportionsstudie nach Vitruv

Auch der Herausgeber dieser Euklid-Ausgabe, der Franziskanermönch Luca Pacioli di Borgo San Sepolcro (1445–1514), der an der Universität von Perugia Mathematik lehrte, hatte sich intensiv mit dem Goldenen Schnitt befasst. Er nannte diese Streckenteilung Göttliche Teilung, was sich auf Platons Identifizierung der Schöpfung mit den fünf platonischen Körpern bezog, zu deren Konstruktion der Goldene Schnitt ein wichtiges Hilfsmittel darstellt. Sein gleichnamiges Werk „De Divina Proportione“ von 1509 besteht aus drei unabhängigen Büchern. Bei dem ersten handelt es sich um eine rein mathematische Abhandlung, die jedoch keinerlei Bezug zur Kunst und Architektur herstellt. Das zweite ist ein kurzer Traktat über die Schriften des Römers Vitruv aus dem 1. Jahrhundert v. Chr. zur Architektur, in denen Vitruv die Proportionen des menschlichen Körpers als Vorlage für Architektur darstellt. Dieses Buch enthält eine Studie von Leonardo da Vinci (1452–1519) über den vitruvianischen Menschen. Das Verhältnis von Quadratseite zu Kreisradius in diesem berühmten Bild entspricht mit einer Abweichung von 1,7 % dem Goldenen Schnitt, der jedoch im zugehörigen Buch gar nicht erwähnt wird. Darüber hinaus würde man diese Abweichung bei einem konstruktiven Verfahren nicht erwarten.

Im Oktober 1597 stellte Johannes Kepler in einem Brief an seinen früheren Tübinger Professor Michael Maestlin die Frage, warum es nur eine einzige mögliche Lösung gebe für die Aufgabe, ein rechtwinkliges Dreieck zu konstruieren, bei dem das Verhältnis der kürzeren zur längeren Seite dem der längeren zur Hypotenuse entspricht. Auf das Original dieses Briefes notierte Maestlin eine Berechnung, die die Hypotenuse einmal mit 10 und einmal mit 10.000.000, und für den letzteren Fall dann die kürzeste Seite mit 7.861.514 und die längere Seite mit 6.180.340 beziffert. Das entspricht einer bis auf die sechste Nachkommastelle genauen (und bis zur fünften korrekten) Angabe des Goldenen Schnitts und ist nach älteren sexagesimalen Berechnungen der Antike die erste bekannte dezimale Angabe dieser Art.^[9]

19. und 20. Jahrhundert

In Abhandlungen verschiedener Autoren im 19. Jahrhundert, insbesondere von dem Philosophen Adolf Zeising^[10], wurden diese beiden Schriften zu der These kombiniert, Pacioli hätte in der „De Divina Proportione” in Zusammenarbeit mit Leonardo da Vinci einen Zusammenhang zwischen Kunst und Goldenem Schnitt hergestellt und damit seine Wiederentdeckung für die Malerei der Renaissance begründet. Zeising war von der Existenz eines Naturgesetzes der Ästhetik überzeugt, dessen Basis der Goldene Schnitt sein müsse. Er suchte und fand den Goldenen Schnitt überall. Seine Schriften verbreiteten sich rasch und begründeten eine wahre Euphorie bezüglich des Goldenen Schnitts. Andererseits zeigt eine Untersuchung der Literatur, dass vor Zeising niemand in den Werken der Antike oder Renaissance den Goldenen Schnitt zu erkennen glaubte. Entsprechende Funde sind daher heute unter Kunsthistorikern eher umstritten.

Die Bezeichnung Goldener Schnitt wurde erstmals 1835 von Martin Ohm (1792–1872; Bruder von Georg Simon Ohm) in einem Lehrbuch der Mathematik verwendet.^[11][12] Auch die Bezeichnung sectio aurea entstand erst in dieser Zeit.

Gustav Theodor Fechner, ein Begründer der experimentellen Psychologie, stellte 1876 bei Untersuchungen mit Versuchspersonen anhand von Rechtecken in der Tat eine Präferenz für den Goldenen Schnitt fest.^[13] Die Ergebnisse bei der Streckenteilung und bei Ellipsen fielen jedoch anders aus. Neuzeitliche Untersuchungen zeigen, dass das Ergebnis solcher Experimente stark vom Kontext der Darbietung abhängt. Fechner fand ferner bei Vermessungen von Bildern in verschiedenen Museen Europas, dass die Seitenverhältnisse im Hochformat im Mittel etwa 4:5 und im Querformat etwa 4:3 betragen und sich damit deutlich vom Goldenen Schnitt unterscheiden.

Der rumänische Diplomat Matila Ghyka verband in seinen Schriften Esthétique des Proportions (1927) und Le nombre d'or (1931) den religiösen Aspekt von Pacioli mit dem ästhetischen von Zeising. Er interpretierte den Goldenen Schnitt als fundamentales Geheimnis des Universums und führte dazu vor allem Beispiele in der Natur an.

Ende des 20. Jahrhunderts suchte die Kunsthistorikerin Marguerite Neveux mit röntgenanalytischen Verfahren unter der Farbe von Originalgemälden, die angeblich den Goldenen Schnitt enthalten, vergeblich nach entsprechenden Markierungen oder Konstruktionsspuren.^[14][15]

Die Bedeutung des Goldenen Schnitts

Vergleich mit anderen Teilungsverhältnissen

Die folgende Abbildung vergleicht verschiedene Rechtecke mit prominenten Seitenverhältnissen in der Umgebung von Φ. Angegeben ist jeweils das Verhältnis von Höhe zu Breite und der entsprechende Zahlenfaktor:

Papier- und Bildformate

Im Buchdruck wurde früher gelegentlich die Nutzfläche einer Seite, der so genannte Satzspiegel, so positioniert, dass das Verhältnis von Bundsteg zu Kopfsteg zu Außensteg zu Fußsteg sich wie 2:3:5:8 verhielt. Diese Wahl von Fibonacci-Zahlen approximiert den Goldenen Schnitt.

Typische Einsatzgebiete der obigen prominenten Seitenverhältnisse (von links nach rechts) sind:

• 4 : 3 – Traditionelles Fernsehformat und Ballenformat für Packpapier. Auch bei älteren Computermonitoren verwendet (z. B.: 1024 × 768 Pixel). Dieses Format geht zurück auf Thomas Alva Edison, der 1889 das Format des klassischen Filmbildes (35-mm-Film) auf 24 × 18 mm festlegte.
• √2 : 1 – Das Seitenverhältnis beim DIN-A4-Blatt und verwandten DIN- / EN- / ISO-Maßen. Bei einer Halbierung durch einen Schnitt, der die längeren Seiten des Rechtecks halbiert, entstehen wiederum Rechtecke mit demselben Seitenverhältnis.
• 3 : 2 – Seitenverhältnis beim Kleinbildfilm (36 mm × 24 mm).
• Φ : 1 – Seitenverhältnis im Goldenen Schnitt. Entspricht dem historischen Buchformat Oktav. Im Bild approximiert mit 144 Pixel × 89 Pixel (theoretischer Fehler nur 5 · 10⁻⁵). Die beiden benachbarten Rechtecke 3:2 und 5:3 haben Seitenverhältnisse von aufeinander folgenden Fibonacci-Zahlen und approximieren daher ebenfalls den Goldenen Schnitt vergleichsweise gut.
• 5 : 3 – Findet neben dem noch breiteren 1 : 1,85 als Kinofilmformat Verwendung.
• 16 : 9 – Breitbildfernsehen.
• 16 : 10 – Manche Computerbildschirme. Diese passen fast zum Goldenen Schnitt (1 : 1,6)

Proportionslehre

Architektur

Frühe Hinweise auf die vermutlich unbewusste Verwendung des Goldenen Schnittes stammen aus der Architektur. Die Schriften des griechischen Geschichtsschreibers Herodot zur Cheops-Pyramide werden gelegentlich dahingehend ausgelegt, dass die Höhe der Seitenfläche zur Hälfte der Basiskante im Verhältnis des Goldenen Schnittes stünde.^{[* 2]} Die entsprechende Textstelle ist jedoch nur interpretierbar. Andererseits wird auch die These vertreten, dass das Verhältnis 2:π für Pyramidenhöhe zu Basiskante die tatsächlichen Maße noch besser widerspiegele. Der Unterschied beider Thesen beträgt 3,0 %.

Viele Werke der griechischen Antike werden als Beispiele für die Verwendung des Goldenen Schnittes angesehen wie beispielsweise die Vorderfront des 447–432 v. Chr. unter Perikles erbauten Parthenon-Tempels auf der Athener Akropolis.^{[* 3]} Da zu diesen Werken keine Pläne überliefert sind, ist nicht bekannt, ob diese Proportionen bewusst oder intuitiv gewählt wurden. Auch in späteren Epochen finden sich zahlreiche Beispiele für die goldene Proportion, wie etwa der Dom von Florenz^{[* 4]}, die Notre Dame in Paris oder die Torhalle in Lorsch (770 n. Chr.)^{[* 5]} . Es gibt jedoch keinen empirischen Nachweis für eine signifikant größere Häufigkeit des Goldenen Schnittes in diesen Epochen im Vergleich zu anderen Teilungsverhältnissen. Ebenso fehlen historische Belege für eine absichtliche Verwendung des Goldenen Schnittes.

Ein Beispiel für die bewusste Umsetzung des Goldenen Schnitts ist das Alte Rathaus in Leipzig, ein Renaissancebau aus den Jahren 1556/57. Der aus der Mittelachse gerückte Rathausturm galt als architektonische Avantgardeleistung der damaligen Zeit und stand mit dem dadurch verursachten Wirbel und Aufruhr für das städtische Selbstbewusstsein der Stadt. Auch dem Stadtgrundriss des nordhessischen Bad Arolsen liegt der Goldene Schnitt zugrunde. Er erstreckt sich vom Schloss über die gesamte, geplante Barockstadt. Hier wurde der Goldene Schnitt allerdings dazu verwendet, die göttliche Ordnung auf Erden und damit die Erhabenheit des damaligen absolutistischen Fürsten aufzuzeigen.

Der Architekt und Maler Le Corbusier (1887–1965) entwickelte ab 1940 ein einheitliches Maßsystem basierend auf den menschlichen Maßen und dem Goldenen Schnitt. Er veröffentlichte es 1949 in seiner Schrift Der Modulor, die zu den bedeutendsten Schriften der Architekturgeschichte beziehungsweise -theorie gezählt wird. Bereits 1934 wurde ihm für die Anwendung mathematischer Ordnungsprinzipien von der Universität Zürich der Titel doctor honoris causa der mathematischen Wissenschaften verliehen.^{[* 6]}

Bildkomposition

Überlagerung eines Goldenen Dreiecks mit der Mona Lisa

Inwieweit die Verwendung des Goldenen Schnittes in der Kunst zu besonders ästhetischen Ergebnissen führt, ist letztlich eine Frage der jeweils herrschenden Kunstauffassung. Für die generelle These, dass diese Proportion besonders ansprechend und harmonisch empfunden wird, gibt es keine gesicherten Belege. Viele Künstler setzten den Goldenen Schnitt bewusst ein, bei vielen Werken wurden Kunsthistoriker erst im Nachhinein fündig. Diese Befunde sind jedoch angesichts der Fülle von Kandidaten für den Goldenen Schnitt, wie man sie beispielsweise in einem reich strukturierten Gemälde finden kann, oft umstritten.

So werden zahlreichen Skulpturen griechischer Bildhauer, wie der Apollo von Belvedere, der Leochares (um 325 v. Chr.) zugeschrieben wird, oder Werke von Phidias (5. Jahrhundert v. Chr.) als Beispiele für die Verwendung des Goldenen Schnittes angesehen. Auf letzteren bezieht sich auch die heute oft übliche Bezeichnung Φ für den Goldenen Schnitt, die von dem amerikanischen Mathematiker Mark Barr eingeführt wurde. Die ebenfalls gelegentlich verwendete Bezeichnung τ bezieht sich dagegen auf das griechische Wort tome für „Schnitt“.

Der Goldene Schnitt wird auch in vielen Gemälden der Renaissance vermutet, wie bei Raffael, Leonardo da Vinci und Albrecht Dürer, zum Beispiel bei da Vincis Das Abendmahl^[16] von 1495, bei Dürers Selbstbildnis von 1500 und seinem Kupferstich Melencolia I von 1514.^{[* 7]}

Künstler der Neuzeit, die den Goldenen Schnitt bewusst einsetzten, sind beispielsweise Mondrian, Paul Signac und Georges Seurat, Hergé oder auch die Künstler der Section d’Or.

Auch in der Fotografie wird der Goldene Schnitt zur Bildgestaltung eingesetzt. Als Faustformel verwendet man hier die Drittel-Regel.^[17][18]

Akustik und Musik

Intervalle

In der Musik werden Töne als konsonant empfunden, wenn das Verhältnis ihrer Schwingungsfrequenzen ein Bruch aus kleinen ganzen Zahlen ist.

Tonleitern mit irrationalen Schwingungsverhältnissen, wie beispielsweise dem des Goldenen Schnittes, spielen daher allenfalls in der experimentellen Musik oder in speziellen Kulturkreisen eine Rolle.

Dass eine Annäherung dieses Verhältnisses zum Goldenen Schnitt hin nicht unbedingt zu einem wohlklingenden Intervall führt, lässt sich daran erkennen, dass unter den Tonintervallen, deren Schwingungsverhältnis aufeinanderfolgenden Fibonacci-Zahlen entspricht, höchstens die Quinte mit einem Schwingungsverhältnis von 3:2 herausragt. Die große Terz mit einem Schwingungsverhältnis von 5:4 wird schon als harmonischer empfunden als die große Sexte mit 5:3 und die kleine Sexte mit 8:5. Da ein Tonintervall im Goldenen Schnitt nur etwa 19 Cent größer ist als eine kleine Sexte, ist es für ein wenig geschultes Ohr nur schwer von dieser zu unterscheiden ( Audiobeispiel^?/i).

Komposition

Der Goldene Schnitt wird gelegentlich auch in Strukturkonzepten von Musikstücken vermutet. So hat der ungarische Musikwissenschaftler Ernö Lendvai versucht, den Goldenen Schnitt als wesentliches Gestaltungsprinzip der Werke Béla Bartóks nachzuweisen. Seiner Ansicht nach hat Bartók den Aufbau seiner Kompositionen so gestaltet, dass die Anzahl der Takte in einzelnen Formabschnitten Verhältnisse bilden, die den Goldenen Schnitt approximieren. Allerdings sind seine Berechnungen umstritten.^{[* 8]}

In der Musik nach 1945 finden sich Beispiele für die bewusste Proportionierung nach den Zahlen der Fibonacci-Reihe, etwa im Klavierstück IX von Karlheinz Stockhausen oder in den Werken Gérard Griseys.

Instrumentenbau

Goldener Schnitt von Martina Schettina (2009)

Der Goldene Schnitt wird gelegentlich im Musikinstrumentenbau verwendet. Insbesondere beim Geigenbau soll er für besonders klangschöne Instrumente bürgen. So wird auch behauptet, dass der berühmte Geigenbauer Stradivari den Goldenen Schnitt verwendete, um die klanglich optimale Position der F-Löcher für seine Violinen zu berechnen. Diese Behauptungen basieren jedoch lediglich auf nachträglichen numerischen Analysen von Stradivaris Instrumenten. Ein Nachweis, dass Stradivari bewusst den goldenen Schnitt zur Bestimmung ihrer Proportionen angewandt hat, existiert jedoch nicht.^[19][20]

Zeitgenössische bildende Kunst

In der zeitgenössischen bildenden Kunst wird der Goldene Schnitt nicht nur als Gestaltungsmerkmal verwendet, sondern in manchen Arbeiten selbst Thema oder zentraler Bildinhalt. Der Künstler Jo Niemeyer verwendet den Goldenen Schnitt als grundlegendes Gestaltungsprinzip in seinen Werken, die der konkreten Kunst zugeordnet werden.^[21] Die Künstlerin Martina Schettina thematisiert den goldenen Schnitt in ihren Arbeiten zum Fünfeck, bei welchem die Diagonalen einander im goldenen Schnitt teilen.^[22] Auch visualisiert sie Konstruktionsmethode und Formeln zum Goldenen Schnitt.^[23]

Vorkommen in der Natur

Biologie

Anordnung von Blättern im Abstand des Goldenen Winkels von oben betrachtet. Das Sonnenlicht wird optimal genutzt.

Das spektakulärste Beispiel für Verhältnisse des Goldenen Schnitts in der Natur findet sich bei der Anordnung von Blättern (Phyllotaxis) und in Blütenständen mancher Pflanzen.^{[* 9]} Bei diesen Pflanzen teilt der Winkel zwischen zwei aufeinander folgenden Blättern den Vollkreis von 360° im Verhältnis des Goldenen Schnittes, wenn man die beiden Blattwurzeln durch eine Parallelverschiebung eines der Blätter entlang der Pflanzenachse zur Deckung bringt. Es handelt sich um den Goldenen Winkel von etwa 137,5°.

Die daraus entstehenden Strukturen werden auch als selbstähnlich bezeichnet, insofern ein Muster auf einer tieferen Strukturebene sich in höheren Ebenen wiederfindet.

Beispiele sind die Sonnenblume^{[* 10]}, Kohlarten, Kiefernnadeln an jungen Ästen, Zapfen^{[* 11]}, Agaven, viele Palmen- und Yuccaarten und die Blütenblätter der Rose, um nur einige zu nennen.

Ursache ist das Bestreben dieser Pflanzen, ihre Blätter auf Abstand zu halten. Es wird vermutet, dass sie dazu an jeder Blattwurzel einen besonderen Wachstumshemmer (Inhibitor) erzeugt, der im Pflanzenstamm – vor allem nach oben, in geringerem Umfang aber auch in seitlicher Richtung – diffundiert. Dabei bilden sich in verschiedene Richtungen bestimmte Konzentrationsgefälle aus. Das nächste Blatt entwickelt sich an einer Stelle des Umfangs, wo die Konzentration minimal ist. Dabei stellt sich ein bestimmter Winkel zum Vorgänger ein. Würde dieser Winkel den Vollkreis im Verhältnis einer rationalen Zahl $\tfrac{m}{n}$ teilen, dann würde dieses Blatt genau in die gleiche Richtung wachsen wie dasjenige n Blätter zuvor. Der Beitrag dieses Blattes zur Konzentration des Inhibitors ist aber an dieser Stelle gerade maximal. Daher stellt sich ein Winkel mit einem Verhältnis ein, das alle rationalen Zahlen meidet. Die Zahl ist nun aber gerade die Goldene Zahl (siehe oben). Da bisher kein solcher Inhibitor isoliert werden konnte, werden auch andere Hypothesen diskutiert, wie beispielsweise die Steuerung dieser Vorgänge in analoger Weise durch Konzentrationsverteilungen von Nährstoffen.

Der Nutzen für die Pflanze könnte darin bestehen, dass auf diese Weise von oben einfallendes Sonnenlicht (bzw. Wasser und Luft) optimal genutzt wird^{[* 12]}, eine Vermutung, die bereits Leonardo da Vinci äußerte, oder auch im effizienteren Transport der durch Photosynthese entstandenen Kohlenhydrate im Phloemteil der Leitbündel nach unten. Die Wurzeln von Pflanzen weisen den Goldenen Winkel weniger deutlich auf. Bei anderen Pflanzen wiederum treten Blattspiralen mit anderen Stellungswinkeln zutage. So wird bei manchen Kakteenarten ein Winkel von 99,5° beobachtet, der mit der Variante der Fibonacci-Folge 1, 3, 4, 7, 11, … korrespondiert. In Computersimulationen des Pflanzenwachstums lassen sich diese verschieden Verhaltensweisen durch geeignete Wahl der Diffusionskoeffizienten des Inhibitors provozieren.

Fichtenzapfen mit 5, 8 und 13 Fibonacci-Spiralen

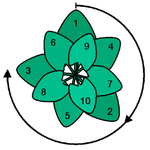
Bei vielen nach dem Goldenen Schnitt organisierten Pflanzen bilden sich in diesem Zusammenhang so genannte Fibonacci-Spiralen aus. Spiralen dieser Art sind besonders gut zu erkennen, wenn der Blattabstand im Vergleich zum Umfang des Pflanzenstammes besonders klein ist. Sie werden nicht von aufeinander folgenden Blättern gebildet, sondern von solchen im Abstand n, wobei n eine Fibonacci-Zahl ist. Solche Blätter befinden sich in enger Nachbarschaft, denn das n-fache des Goldenen Winkels Ψ ist ungefähr ein Vielfaches von 360° wegen

$n\Psi=n\frac{360^\circ}{\Phi}\approx n\frac{m}{n}360^\circ=m\,360^\circ\,,$

wobei m die nächstkleinere Fibonacci-Zahl zu n ist. Da jedes der Blätter zwischen diesen beiden zu einer anderen Spirale gehört, sind n Spiralen zu sehen. Ist $\tfrac{n}{m}$ größer als Φ so ist das Verhältnis der beiden nächsten Fibonacci-Zahlen kleiner und umgekehrt. Daher sind in beide Richtungen Spiralen zu aufeinander folgenden Fibonaccizahlen zu sehen. Der Drehsinn der beiden Spiralentypen ist dem Zufall überlassen, sodass beide Möglichkeiten gleich häufig auftreten.

Sonnenblume mit 34 und 55 Fibonacci-Spiralen

Berechneter Blütenstand mit 1000 Samen im Goldenen Winkel – Es stellen sich 13, 21, 34 und 55 Fibonacci-Spiralen ein.

Besonders beeindruckend sind Fibonacci-Spiralen in Blütenständen, wie beispielsweise bei Sonnenblumen.^{[* 13]} Pflanzenarchitektonisch entsprechen den einzelnen Samen Blätter, wobei jedes einzelne einem eigenen Kreis um den Mittelpunkt des Blütenstandes zugeordnet werden kann, so als hätte man einen Pflanzenstamm mit seinen Blättern wie ein Teleskop zusammengeschoben. Wachstumstechnisch aufeinander folgende Samen liegen daher räumlich weit auseinander, während direkte Nachbarn wieder einen Abstand entsprechend einer Fibonacci-Zahl haben. Im äußeren Bereich von Sonnenblumen zählt man 34 und 55 Spiralen, bei größeren Exemplaren 55 und 89 oder sogar 89 und 144. Die Abweichung vom mathematischen Goldenen Winkel, die in diesem Fall nicht überschritten wird, beträgt weniger als 0,01 %.

Der Goldene Schnitt ist außerdem in radiärsymmetrischen fünfzähligen Blüten erkennbar wie beispielsweise bei der Glockenblume, der Akelei und der (wilden) Hecken-Rose. Der Abstand der Spitzen von Blütenblättern nächster Nachbarn zu dem der übernächsten steht wie beim regelmäßigen Fünfeck üblich in seinem Verhältnis. Das betrifft ebenso Seesterne und andere Tiere mit fünfzähliger Symmetrie.^{[* 14]}

Goldener Schnitt im Efeublatt

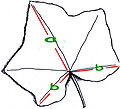
Darüber hinaus wird der Goldene Schnitt auch im Verhältnis der Längen aufeinander folgender Stängelabschnitte mancher Pflanzen vermutet wie beispielsweise bei der Pappel. Auch im Efeublatt stehen die Blattachsen a und b (siehe Abbildung) ungefähr im Verhältnis des Goldenen Schnittes. Diese Beispiele sind jedoch umstritten.

Noch im 19. Jahrhundert war die Ansicht weit verbreitet, der Goldene Schnitt sei ein göttliches Naturgesetz und in vielfacher Weise auch in den Proportionen des menschlichen Körpers realisiert. So nahm Adolf Zeising in seinem Buch über die Proportionen des menschlichen Körpers^[10] an, dass der Nabel die Körpergröße im Verhältnis des Goldenen Schnitts teile, und der untere Abschnitt werde durch das Knie wiederum so geteilt. Ferner scheinen die Verhältnisse benachbarter Teile der Gliedmaßen wie beispielsweise bei Ober- und Unterarm sowie bei den Fingerknochen ungefähr in diesem Verhältnis zu stehen. Eine genaue Überprüfung ergibt jedoch Streuungen der Verhältnisse im 20-%-Bereich. Oft enthält auch die Definition, wie beispielsweise die Länge eines Körperteils exakt zu bestimmen sei, eine gewisse Portion Willkür. Ferner fehlt dieser These bis heute eine wissenschaftliche Grundlage. Es dominiert daher weitgehend die Ansicht, dass diese Beobachtungen lediglich die Folge gezielter Selektion von benachbarten Paaren aus einer Menge von beliebigen Größen sind.^{[* 15]}

Bahnresonanzen

Seit langem ist bekannt, dass die Umlaufzeiten mancher Planeten und Monde in Verhältnis kleiner ganzer Zahlen stehen wie beispielsweise Jupiter und Saturn mit 2:5 oder die Jupitermonde Io, Ganymed und Europa mit 1:2:4. Derartige Bahnresonanzen stabilisieren die Bahnen der Himmelskörper langfristig gegen kleinere Störungen. Erst 1964 wurde entdeckt, dass auch hinreichend irrationale Verhältnisse, wie sie beispielsweise im Fall 1:Φ vorliegen würden, stabilisierend wirken können. Derartige Bahnen werden KAM-Bahnen (siehe Kolmogorow-Arnold-Moser-Theorem) genannt, wobei die drei Buchstaben für die Namen der Entdecker Andrei Kolmogorow, V. I. Arnold und Jürgen Moser stehen.^[24][25]

Kristallstrukturen

Der Goldene Schnitt tritt auch bei den Quasikristallen der Festkörperphysik in Erscheinung, die 1984 von Dan Shechtman und seinen Kollegen entdeckt wurden.^[26] Dabei handelt es sich um Strukturen mit fünfzähliger Symmetrie, aus denen sich aber, wie bereits Kepler erkannte, keine streng periodischen Kristallgitter aufbauen lassen, wie dies bei Kristallen üblich ist. Entsprechend groß war die Überraschung, als man bei Röntgenstrukturanalysen Beugungsbilder mit fünfzähliger Symmetrie fand. Diese Quasikristalle bestehen strukturell aus zwei verschieden rhomboedrischen Grundbausteinen, mit denen man den Raum zwar lückenlos, jedoch ohne globale Periodizität füllen kann (Penrose-Parkettierung). Beide Rhomboeder setzten sich aus den gleichen rautenförmigen Seitenflächen zusammen, die jedoch unterschiedlich orientiert sind. Die Form dieser Rauten lässt sich nun dadurch definieren, dass ihre Diagonalen im Verhältnis des Goldenen Schnittes stehen.

Informatik

In der Informatik speichert man Daten in Hashtabellen, um darauf schnell zuzugreifen. Die Position h(k), an der ein Datensatz k in der Tabelle gespeichert wird, berechnet man durch eine Hashfunktion h. Für einen effizienten Zugriff müssen die Datensätze möglichst gleichmäßig verteilt in die Tabelle geschrieben werden. Eine Variante für die Hashfunktion ist die multiplikative Methode, bei der die Hashwerte für eine Tabelle der Größe m nach der folgenden Formel berechnet werden:

$h(k) = \lfloor m (k A - \lfloor k A \rfloor)\rfloor$.

Dabei stellen $\lfloor \ldots \rfloor$ Gaußklammern dar, die den Klammerinhalt auf die nächste ganze Zahl abrunden. Der angesehene Informatiker Donald Ervin Knuth schlägt für die frei wählbare Konstante A = 1 / Φ vor, um eine gute Verteilung der Datensätze zu erhalten.^[27]

Eine weitere Verbindung zwischen der Informationstheorie und dem Goldenen Schnitt wurde durch Helmar Frank mit der Definition der Auffälligkeit hergestellt. Er konnte zeigen, dass der mathematische Wert des Maximums der Auffälligkeit sehr nah an das Verhältnis des Goldenen Schnitts herankommt.

Siehe auch

• Harmonische Teilung, eine weitere Teilung der Ästhetik
• Mathematische Konstanten
• Liste besonderer Zahlen

Literatur

Historische Literatur

• Luca Pacioli; Constantin Winterberg (Hg. u. Übers.): Divina Proportione. Venedig 1509. Carl Graeser, Wien 1889 (im Internet-Archiv: [1], bei alo: [2])
• Martin Ohm: Lehrbuch der gesammten höhern Mathematik. Band 2. Friedrich Volckmar, Leipzig 1839 (bei Google Books: [3], [4])
• Adolf Zeising: Neue Lehre von den Proportionen des menschlichen Körpers. Rudolph Weigel, Leipzig 1854 (bei Google Books: [5])
• Adolf Zeising: Das Normalverhältniss der chemischen und morphologischen Proportionen. Rudolph Weigel, Leipzig 1856 (bei Google Books: [6])
• Gustav Theodor Fechner: Zur experimentalen Ästhetik. Hirzel, Leipzig 1871.

Neuere Literatur

• Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg, Berlin, Oxford 1996. ISBN 3-86025-404-9.
• Priya Hemenway: Divine Proportion. Phi in Art, Nature and Science. Sterling, New York 2005, ISBN 1-4027-3522-7. (Priya Hemenway: Der Geheime Code: Die rätselhafte Formel, die Kunst, Natur und Wissenschaft bestimmt. Taschen Verlag, Köln 2008, ISBN 978-3-8365-0708-0.)
• Roger Herz-Fischler: A mathematical History of the Golden Ratio. Dover Publications, New York 1998, ISBN 0-486-40007-7.
• Jürgen Fredel: Maßästhetik. Studien zu Proportionsfragen und zum Goldenen Schnitt. Lit, Hamburg 1998, ISBN 3-8258-3408-5.
• Albert van der Schoot: Die Geschichte des goldenen Schnitts. Frommann-Holzboog, Stuttgart 2005, ISBN 3-7728-2218-5.
• Hans Walser: Der Goldene Schnitt. Teubner, Stuttgart 1993. ISBN 3-8154-2511-5.

Weblinks

 Commons: Goldener Schnitt – Sammlung von Bildern, Videos und Audiodateien

• Marcus Frings: Der Goldene Schnitt und The Golden Section in Architectural Theory (kritische Analysen)
• Ruben Stelzner: Der Goldene Schnitt und das Mysterium der Schönheit, 2002
• Der Goldene Schnitt in der Biologie (englisch)
• Fibonacci-Reihen und Goldener Schnitt bei Beobachtung und Simulation biologischer Systeme (englisch)
• Bilder zum Goldenen Schnitt in der Biologie
• Bernhard Peter: Goldener Schnitt – Mathematik und Bedeutung in der Kunst (insbes. 34 verschiedene Konstruktionverfahren)
• Video mit Prof. Albrecht Beutelspacher (Video-Archiv)
• Folge A001622 in OEIS (Dezimalentwicklung von Φ)
• Folge A028259 in OEIS (Engel-Entwicklung von Φ)
• Folge A118242 in OEIS (Pierce-Entwicklung von 1/Φ)

Einzelnachweise

1. ↑ Forum Geometricorum Volume 5 (2005) 135–136.
2. ↑ Die hier auftretende Abweichung ist ungefähr 16-mal kleiner als die durch den Dirichletscher Approximationssatz garantierte (nämlich $\tfrac{1}{49}$). Bei der Näherung von Φ durch $\tfrac{13}{8}$ ist die Abweichung dagegen nur 2,2-mal kleiner als $\tfrac{1}{64}$.
3. ↑ a) Bruce Ikenaga: Rational Approximation by Continued Fractions (abgerufen 3. Dezember 2009), b) Serge Lang: Introduction to Diophantine Approximations, Springer-Verlag 1995, S. 9, c) Ivan Niven, Herbert S. Zuckermann, Hugh L. Montgomery: An Introduction to the Theory of Numbers. Wiley, 1960, 5. Auflage 1991, ISBN 0-471-54600-3, S. 338 (Theorem 7.13). Man beachte aber: dieser Satz schließt nicht aus, dass es außer diesen Brüchen $\tfrac{p}{q}$ nicht noch weitere beste Approximationen geben kann. Zum Beispiel approximiert $\tfrac{13}{4}$ die Zahl π besser als 3 und $\tfrac{311}{99}$ approximiert π besser als $\tfrac{22}{7}$.
4. ↑ The Golden ratio. In: MacTutor History of Mathematics archive (englisch)
5. ↑ Leonardo da Pisa, Liber abbaci (cap. I, 7, dort unter anderen Aufgaben: Quot paria coniculorum in uno anno ex uno pario germinentur), hrsg. von Baldassare Boncompagni, Scritti di Leonardo Pisano matematico del secolo decimoterzo, Band I, Roma: Tipografia delle scienze matematiche e fisiche, 1857, S. 283f., Wiedergabe der Handschrift Florenz, Cod. magliabechiano cs cI, 2626, fol. 123v-124r, bei Heinz Lüneburg, Leonardi Pisani Liber Abbaci oder Lesevergnügen eines Mathematikers, 2. überarb. und erw. Ausg., Mannheim u. a.: BI Wissenschaftsverlag, 1993, ISBN 3-411-15462-4, nach S. 252; Wiedergabe des lateinischen Textes der Kaninchenaufgabe u. a. bei Bernd Thaller, Leonardo und der Goldene Schnitt (8. Dezember 2009, PDF), mit engl. Übersetzung bei Roberto Bignoni, The Golden Number – 3 –.
6. ↑ Formalisierte Wiedergabe nach Heinz Lüneburg, Leonardi Pisani Liber Abbaci oder Lesevergnügen eines Mathematikers, 2. überarb. und erw. Ausg., Mannheim u.a.: BI Wissenschaftsverlag, 1993, ISBN 3-411-15462-4, S. 298
7. ↑ Leonardo da Pisa, Liber abbaci, cap. 15, ed. Boncompagni S. 438, zu finden auch schon in der Wiedergabe von cap. 15 bei Guillaume Libri, Histoire des sciences mathématiques in Italie, Band II, Paris: Jules Renouard et C.ie, 1838, S. 430 (Auszug in der Google Buchsuche)
8. ↑ Leonard Curchin / Roger Herz-Fischler, De quand date le premier rapprochement entre la suite de Fibonacci et la division en extrême et moyenne raison?, in: Centaurus 28,2 (1985), S. 129–138, S. 130
9. ↑ Roger Herz-Fischler, A mathematical History of the Golden Ratio, Dover Publications, Minneola (New York) 1998, S. 158 (Section 31.J.iii)
10. ↑ ^{a b} Lit.: Zeising, 1854
11. ↑ Lit.: Ohm, 1835
12. ↑ The Golden ratio. In: MacTutor History of Mathematics archive (englisch)
13. ↑ Lit.: Fechner, 1876
14. ↑ Lit.: Neveux, 1995
15. ↑ Marguerite Neveux : « Le nombre d'or est une affabulation ». Webseite von La Recherche (populärwissenschaftliche Zeitschrift) (abgerufen 1. November 2011)
16. ↑ Bernhard Peter: Der Goldene Schnitt in Leonardos Abendmahl auf www.dr-bernhard-peter.de (abgerufen 1. November 2011)
17. ↑ Michael Frye: Digitale Landschaftsfotografie: Fotografieren wie Ansel Adams und Co. Hüthig Jehle Rehm 2010, ISBN 978-3-8266-5896-9, S. 72 (Auszug in der Google Buchsuche)
18. ↑ Garry Reynolds: Zen oder die Kunst der Präsentation: mit einfachen Ideen gestalten und präsentieren. Pearson Education 2008, ISBN 978-3-8273-2708-6, S. 151-152 (Auszug in der Google Buchsuche)
19. ↑ How a Violin is Made. In Popular Mechanics, September 1943, S. 106-108 (Auszug in der Google Buchsuche)
20. ↑ Stewart Pollens: Stradivari. Cambridge University Press 2010, ISBN 978-0-521-87304-8, S. 239 (Auszug in der Google Buchsuche)
21. ↑ Bernhard Peter: Der Goldene Schnitt in der konkreten Kunst: Beispiele von Jo Niemeyer auf www.dr-bernhard-peter.de (abgerufen 1. November 2011)
22. ↑ Bilder im virtuellen Mathe-Museum der TU Freiberg
23. ↑ Mathe-Museum TU Freiberg
24. ↑ Siehe Dvorak/Freistetter/Kurths: Chaos and stability in planetary systems (Springer Lecture Notes in Physics, 2006), S. 118–121 und den Wikipedia-Artikel über noble Zahlen.
25. ↑ R. Badii, Remo Badii, A. Politi: Complexity: Hierarchical Structures and Scaling in Physics. Cambridge University Press 1999, ISBN 0-521-66385-7 , S. 46 (Auszug in der Google Buchsuche)
26. ↑ Siehe z.B. das Kapitel Self-Similarity, Fractals, Deterministic Chaos and a New State of Matter in Manfred R. Schroeder: Number theory in science and communication., 5. Auflage, Springer, Berlin u.a., 2009.
27. ↑ Thomas H. Cormen, Charles Leiserson, Ronald Linn Rivest, Clifford Stein: Introduction to Algorithms. 2. Aufl. MIT Press, 2001, ISBN 0-262-53196-8, S. 231–232

---

• Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg, Berlin, Oxford 1996. ISBN 3-86025-404-9

1. ↑ S. 157–161
2. ↑ S. 136–137
3. ↑ S. 138
4. ↑ S. 138–141
5. ↑ S. 138
6. ↑ S. 142–147
7. ↑ S. 148–155
8. ↑ S. 165–167
9. ↑ S. 124
10. ↑ S. 123
11. ↑ S. 128
12. ↑ S. 125
13. ↑ S. 123
14. ↑ S. 128
15. ↑ S. 130–133

Dieser Artikel wurde am 10. August 2004 in dieser Version in die Liste der exzellenten Artikel aufgenommen.