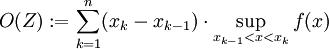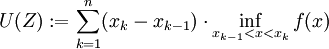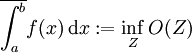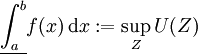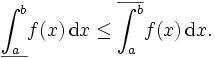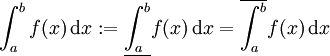Obersumme

Das Riemann-Integral ist eine nach dem deutschen Mathematiker Bernhard Riemann benannte Methode zur Präzisierung der anschaulichen Vorstellung des Flächeninhaltes zwischen der x-Achse und dem Graphen einer Funktion. Der riemannsche Integralbegriff gehört neben dem allgemeineren lebesgueschen zu den beiden klassischen der Analysis.

Das zu Grunde liegende Konzept des Riemann-Integrals besteht darin, den gesuchten Flächeninhalt mit Hilfe des leicht zu berechnenden Flächeninhalts von Rechtecken anzunähern. Man geht dabei so vor, dass man in jedem Schritt zwei Familien von Rechtecken so wählt, dass der Graph der Funktion „zwischen“ ihnen liegt. Indem man sukzessive die Anzahl der Rechtecke erhöht, erhält man mit der Zeit eine immer genauere Annäherung des Funktionsgraphen durch die zu den Rechtecken gehörenden Treppenfunktionen. Entsprechend lässt sich der Flächeninhalt zwischen dem Graphen und der x-Achse durch die Flächeninhalte der Rechtecke approximieren.

Ober- und Untersummen

Dieser Zugang wird meist Jean Gaston Darboux zugeschrieben.

Untersumme (grün) und Obersumme (grün plus lavendel) für eine Zerlegung in vier Teilintervalle

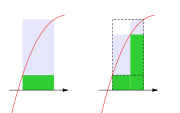
Das Integrationsintervall wird hierbei in kleinere Stücke zerlegt, der gesuchte Flächeninhalt zerfällt dabei in senkrechte Streifen. Für jeden dieser Streifen wird nun einerseits das größte Rechteck betrachtet, das von der x-Achse ausgehend den Graphen nicht schneidet (im Bild grün), und andererseits das kleinste Rechteck, das von der x-Achse ausgehend den Graphen ganz umfasst (im Bild jeweils das grüne Rechteck zusammen mit der grauen Ergänzung darüber). Die Summe der Flächeninhalte der großen Rechtecke wird als Obersumme, die der kleinen als Untersumme bezeichnet. Kann man durch geeignete, ausreichend feine Unterteilung des Integrationsintervalles den Unterschied zwischen Ober- und Untersumme beliebig klein machen, so gibt es nur eine Zahl, die kleiner oder gleich jeder Obersumme und größer oder gleich jeder Untersumme ist, und diese Zahl ist der gesuchte Flächeninhalt, das Riemann-Integral.

Für die mathematische Präzisierung seien im folgenden [a,b] ein Intervall und $f\colon[a,b]\to\R$ eine beschränkte Funktion.

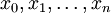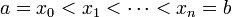Eine Zerlegung Z von [a,b] in n Teile sei eine endliche Folge $x_0,x_1,\ldots,x_n$ mit $a=x_0<x_1<\cdots<x_n=b$. Dann seien die zu dieser Zerlegung gehörende Ober- bzw. Untersumme definiert als

$O(Z):=\sum_{k=1}^n(x_k-x_{k-1})\cdot\sup_{x_{k-1}<x<x_k}f(x)$

$U(Z):=\sum_{k=1}^n(x_k-x_{k-1})\cdot\inf_{x_{k-1}<x<x_k}f(x)$

Die Funktion wird dabei durch die Treppenfunktion ersetzt, die auf jedem Teilintervall konstant gleich dem Supremum bzw. Infimum der Funktion auf diesem Intervall ist.

Bei einer feineren Unterteilung wird die Obersumme kleiner und die Untersumme größer

Bei einer Verfeinerung der Zerlegung wird die Obersumme kleiner, die Untersumme größer (oder sie bleiben gleich). Einer „unendlich feinen“ Zerlegung entsprechen also Infimum der Obersummen sowie Supremum der Untersummen; diese werden als oberes bzw. unteres darbouxsches Integral von f bezeichnet:

$\overline{\int_a^b}f(x)\,\mathrm dx:=\inf_ZO(Z)$

$\underline{\int_a^b}f(x)\,\mathrm dx:=\sup_ZU(Z)$

Dabei werden jeweils alle möglichen Zerlegungen Z des Intervalls in eine beliebige endliche Anzahl von Teilintervallen betrachtet.

Es gilt stets

$\underline{\int_a^b}f(x)\,\mathrm dx\leq\overline{\int_a^b}f(x)\,\mathrm dx.$

Gilt Gleichheit, so heißt f Riemann-integrierbar (oder Darboux-integrierbar), und der gemeinsame Wert

$\int_a^bf(x)\,\mathrm dx:=\underline{\int_a^b}f(x)\,\mathrm dx=\overline{\int_a^b}f(x)\,\mathrm dx$

heißt das Riemann-Integral (oder Darboux-Integral) von f über dem Intervall [a,b].

Ein Beispiel einer nicht Riemann-intergrierbaren Funktion ist die Dirichlet-Funktion, die auf allen rationalen Punkten den Wert 1 annimmt und auf allen irrationalen Punkten den Wert 0.

Uneigentliche Integrale

Als uneigentliche Integrale bezeichnet man:

• Integrale mit den „Intervallgrenzen“ 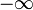$-\infty$ oder $\infty$; dabei ist $\int_{-\infty}^{\infty} f(x) \mathrm{d}x:= \lim_{a,b \rightarrow \infty} \int_{-a}^b f(x) \,\mathrm{d}x.$
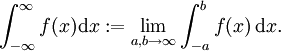
• Integrale mit unbeschränkten Funktionen in einer der Intervallgrenzen; dabei ist 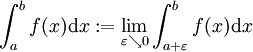$\int_a^b f(x) \mathrm{d}x := \lim_{\varepsilon \searrow 0} \int_{a+\varepsilon}^b f(x) \mathrm{d}x$ bzw. $\int_a^b f(x) \mathrm{d}x := \lim_{\varepsilon \searrow 0} \int_a^{b-\varepsilon} f(x) \,\mathrm{d}x.$

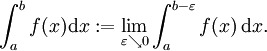
Im Sinne von Isaac Newton, welcher dieses Integral in seinen Philosophiae Naturalis Principia Mathematica zum ersten Male deutlich aussprach, versteht auch Riemann die Existenz des bestimmten Integrales als Grenzwert einer Summe von Rechtecken für den Fall, dass die Breite der Elementarflächen gegen null geht.

Quellen

• Bernhard Riemann: Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe. Habilitationsschrift (1854) mit Begründung des nach ihm benannten Integralbegriffs.
• Harro Heuser: Lehrbuch der Analysis, Teil 1, 9. Aufl., Stuttgart: Teubner, 1991. ISBN 3-519-22231-0 (Insbesondere Abschnitt 82).

Weblinks

• Visualisierung des Riemann-Integrals
• http://archives.math.utk.edu/visual.calculus/4/riemann_sums.4/index.html
• http://www.mathe-online.at/nml/materialien/innsbruck/riemann/