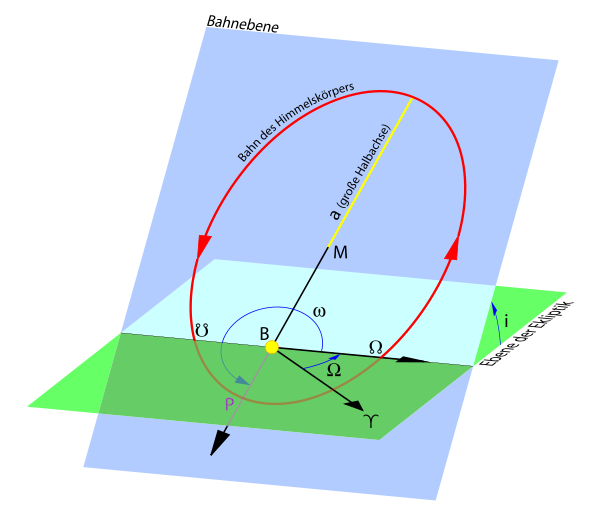
Orbitalebene

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Keplerbahnen sind die Lösungen des Keplerproblems, wie sich ein kleiner Himmelskörper um einen größeren bewegt. Die Lösungen sind die Kegelschnitte Ellipse, Parabel und Hyperbel, die sich in ihrer Gesamtenergie unterscheiden. Der häufigste Fall ist die Keplerellipse, die nach Johannes Kepler den gebundenen Zustand beschreibt, beispielsweise Sonne-Erde, Erde-Mond.

Ideale Keplerbahn

Im Idealfall, dass keine weiteren Körper existieren (Zweikörperproblem), erfolgt die gegenseitige Bewegung nach den drei keplerschen Gesetzen.

Ihre allgemeine Form ist dann:

$r (\varphi) = {p \over { 1 + e \cdot \cos \varphi}}, ~ \varphi \in I$

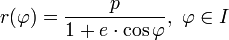
mit der Exzentrizität e und dem Parameter p

Das Intervall I ist abhängig von der Bahn, etwa 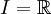$I = \mathbb{R}$ für die Keplerellipse

Sie lässt sich dann exakt durch sechs Bahnelemente beschreiben.

Parabelbahnen und Hyperbelbahnen sind ungebundene Zustände, die bei manchen Kometen vorliegen. Bei diesen Bahnen gibt es nur eine einzige Annäherung, der Komet verschwindet anschließend ohne Wiederkehr aus dem Sonnensystem.

Störende Kräfte

Durch unregelmäßige oder weitere Himmelskörper ist das Schwerefeld jedoch nicht kugelsymmetrisch, wodurch Bahnstörungen entstehen. Auch kleine Bremseffekte durch Gase oder Meteoroiden, durch Strahlungsdruck und gemäß der Relativitätstheorie tragen zu ihnen bei. Dadurch ändern sich die Zahlenwerte der sechs Bahnelemente langsam.

Man kann diese zeitabhängigen oder periodischen Effekte durch die Methode „Variation der Elemente“ berechnen, wobei jede momentane („oskulierende“) Keplerellipse stetig in die nächste übergeht. Die Bahnstörungen können langzeitlich (immer in gleicher Richtung) oder periodisch sein. In der Nähe von irregulär geformten Himmelskörpern oder beim Flug durch Materiewolken treten auch unregelmäßige Effekte auf.

Die Bahnachsen (a) der acht Planeten unseres Sonnensystems bleiben praktisch konstant, weil ihre Massen groß und die Bahnen kreisähnlich sind. Kleinplaneten (Asteroiden) und Kometen können aber gravierende Änderungen erfahren, wenn sie einem Planeten nahekommen. Bei niedrigen künstlichen Erdsatelliten betragen die Bahnstörungen einige Zehntel Grad pro Stunde bzw. einige Kilometer und lassen auf die genaue Form des Geoids schließen.

Streng genommen gelten exakte Keplerbahnen nur für kugelförmige Körper, doch ist diese Bedingung bei größeren Entfernungen in der Astronomie hinreichend erfüllt. Auch für Mondbahnen um stark abgeplattete Planeten (z. B. Jupitermonde) kann man genähert mit Keplers Formeln rechnen, wenn das dritte Keplergesetz um einen kleinen Faktor ergänzt wird. De facto läuft dies (zusätzlich zur Bahnachse a) auf ein siebentes Bahnelement für die Umlaufzeit hinaus.

Siehe auch

• Gravitationsgesetz
• Bahnbestimmung
• Satellitenbahnelement
• Störungsrechnung