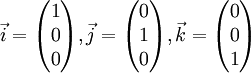Orthogonalbasis

Eine Orthonormalbasis eines Prähilbertraums ist in der linearen Algebra und der Funktionalanalysis eine Basis dieses Vektorraums, deren Elemente normiert (also Einheitsvektoren) und paarweise orthogonal (daher auch Orthonormalbasis) zueinander sind.

Der Begriff ist sowohl im Fall endlicher Dimension als auch für unendlich-dimensionale Räume, insbesondere Hilberträume, von großer Bedeutung.

Endlich-dimensionale Räume

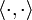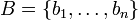Es sei V ein endlichdimensionaler euklidischer Vektorraum mit Skalarprodukt $\langle \cdot, \cdot \rangle$, welches die Norm $\|\cdot\|$ induziert. Unter einer Orthonormalbasis für V versteht man eine Basis $B = \{b_1,\ldots,b_n\}$ von V mit den folgenden Eigenschaften:

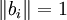• $\|b_i\| = 1$ für alle $i\in\{1,\ldots,n\}$.
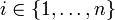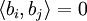• $\langle b_i, b_j \rangle = 0$ für alle 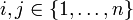$i,j \in\{1,\ldots,n\}$ mit $i \neq j$.

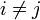Beispielsweise ist die Menge

$\vec i = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix},\vec j = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix},\vec k = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$

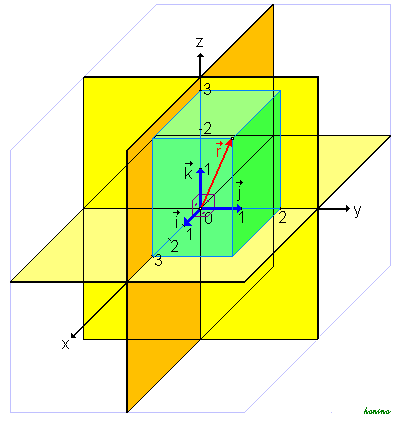
eine Orthonormalbasis für den dreidimensionalen euklidischen Vektorraum $\mathbb{R}^3$ (ausgestattet mit dem Standardskalarprodukt): Sie sind eine Basis des $\mathbb{R}^3$, jeder dieser Vektoren hat die Länge 1, und je zwei dieser Vektoren stehen senkrecht aufeinander, denn ihr Skalarprodukt ist 0.

Die Orthonormalbasis 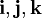${\mathbf{i},\mathbf{j},\mathbf{k}}$ im $\mathbb{R}^3$ und ein mit ihr dargestellter Vektor $\mathbf{r} = 3\mathbf{i} + 2\mathbf{j} + 3\mathbf{k}$

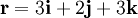
Allgemeiner Fall

(Eine anwendungsorientierte Herleitung zu diesem Thema bietet der Abschnitt zur Verallgemeinerung im Artikel Fouriertransformation)

Im allgemeinen Fall eines Prähilbertraums V unendlicher Dimension, insbesondere eines Hilbertraums, nennt man ein Orthonormalsystem S in V, dessen lineare Hülle dicht in V liegt, vollständig bzw. Orthonormalbasis. Ein vollständiges Orthonormalsystem S hat damit die Eigenschaft, dass für jedes 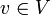$v \in V$ die Fourierentwicklung möglich ist, d. h., es gilt

$v=\sum_{u \in S} \langle v, u \rangle u$.

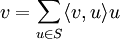Damit ist eine Orthonormalbasis ein wichtiger Spezialfall einer Schauderbasis.

Es ist zu beachten, dass im Sinne dieses Abschnitts, im Gegensatz zur endlichen Dimension, eine Orthonormalbasis keine Basis im üblichen Sinn der linearen Algebra (Hamelbasis) ist, d. h., ein Element aus v lässt sich im Allgemeinen nicht als Linearkombination aus endlich vielen Basisvektoren (Elementen aus S) darstellen, sondern nur mit abzählbar unendlich vielen, also als Reihe. Mit anderen Worten: Die lineare Hülle ist nicht gleich V, liegt aber dicht in V. Jeder Vektorraum besitzt eine Hamelbasis, die aber in vielen Fällen nicht explizit bekannt ist und somit von keinem praktischen Nutzen ist.

Allgemein gelten für Innenprodukträume (Prähilbertäume) und vollständige Innenprodukträume (Hilberträume) folgende Sätze:

• In einem Innenproduktraum V ist ein Orthonormalsystem genau dann eine Orthonormalbasis, wenn die parsevalsche Gleichung

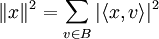$\|x\|^2=\sum_{v\in B}|\langle x,v\rangle|^2$ für alle 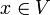$x \in V$ erfüllt ist.

• Jeder (vom Nullraum verschiedene) separable Innenproduktraum besitzt eine Orthonormalbasis, die von höchstens abzählbarer Mächtigkeit ist.
• In einem Hilbertraum V ist ein Orthonormalsystem S genau dann eine Orthonormalbasis, wenn es maximal ist, d. h., wenn für alle 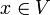$x \in V$ folgende Implikation gilt:

$\left( \langle x, s \rangle = 0 \ \forall s \in S \right) \Rightarrow x=0$,

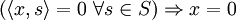mit anderen Worten: Der Nullvektor ist der einzige Vektor, der auf allen Vektoren aus S senkrecht steht.

• Jeder (vom Nullraum verschiedene) Innenproduktraum besitzt maximale Orthonormalsysteme und, wenn er ein Hilbertraum ist, somit auch Orthonormalbasen.
• Ein (vom Nullraum verschiedener) Hilbertraum besitzt genau dann eine abzählbare Orthonormalbasis, wenn er separabel ist.

Insbesondere besitzt also jeder separable und jeder vollständige Innenproduktraum eine Orthonormalbasis.

Siehe auch

• Gram-Schmidtsches Orthogonalisierungsverfahren