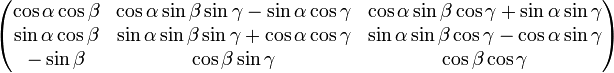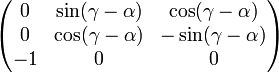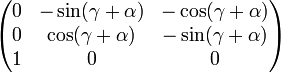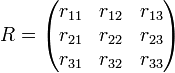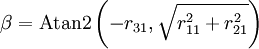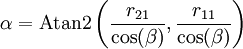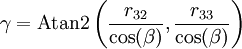Nickwinkel

Orientierung der Achsen bei einem Flugzeug

Orientierung der Achsen bei einem Satelliten

Roll-Pitch-Yaw-Winkel bzw. Roll-Nick-Gier-Winkel sind eine Möglichkeit zur Beschreibung der Orientierung im dreidimensionalen Raum. Die Winkel beschreiben Drehungen um drei rechtwinklig zueinander stehende Achsen.

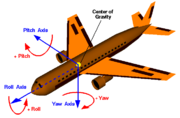
Die Bezeichnung der Achsen stammt aus der Flugsteuerung (siehe Zeichnung rechts). Bei einem Flugzeug zeigt die x-Achse entlang der Flugrichtung (engl. Heading). Senkrecht dazu verläuft die y-Achse in Richtung der rechten Tragfläche. Die z-Achse steht senkrecht auf der x-y-Ebene und weist nach unten (Rechtssystem). Ähnlich sehen die Zuordnungen bei Schiffen und Fahrzeugen aus.

Die Drehungen tragen die Namen:

• Rollen (engl. roll, für den Winkel auch Querneigungswinkel, engl. bank angle), Drehung um die x-Achse (Längsachse)
• Nicken (engl. Pitch), Drehung um die y-Achse (Querachse)
• Gieren (engl. yaw, für die Richtung auch heading oder Azimut), Drehung um die z-Achse (Hochachse/Gierachse)

Auch bei dreiachsenstabilisierten Satelliten, die die Erde mit einer festen Ausrichtung umkreisen, hat sich der Sprachgebrauch für die Kippwinkel eingebürgert (siehe rechtes Bild). Die x-Achse weist in Flugrichtung um die Erde. Die Antennen, die auf die Erde ausgerichtet sind, zeigen entlang der z-Achse. Senkrecht auf der z-x-Ebene drehen sich die Sonnenkollektoren um die y-Achse. Eine Drehung um die z-Achse hat nur geringen Einfluss auf die Orientierung der Antennen zur Erde, weshalb diese Lageregelung mit einem größeren Fehler behaftet sein kann als bei den anderen Achsen. Typische Werte sind für Yaw ±0.15°, für Roll/Pitch ±0.05°.

In der Robotik werden Roll-Pitch-Yaw-Winkel zur Beschreibung von Orientierungen (des Werkzeugs oder anderer Objekte), bezogen auf eine raumfeste Basis, verwendet.

„XYZ-Konvention“

Die Rotationen beziehen sich immer auf die raumfeste Orthogonalbasis. Dabei beschreibt X die Rotation um die x-Achse um den Winkel γ, Y die Rotation um die y-Achse um den Winkel β und Z die Rotation um die z-Achse um den Winkel α.

Die Drehmatrix für diese Definition sieht folgendermaßen aus:

$\begin{pmatrix} \cos \alpha \cos \beta & \cos \alpha \sin \beta \sin \gamma - \sin \alpha \cos \gamma & \cos \alpha \sin \beta \cos \gamma + \sin \alpha \sin \gamma \\ \sin \alpha \cos \beta & \sin \alpha \sin \beta \sin \gamma + \cos \alpha \cos \gamma & \sin \alpha \sin \beta \cos \gamma - \cos \alpha \sin \gamma \\ - \sin \beta & \cos \beta \sin \gamma & \cos \beta \cos \gamma \end{pmatrix}$

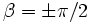Ist $\beta=\pm\pi/2$, tritt eine Singularität auf. Die Drehmatrix ergibt für β = π / 2 mithilfe der Additionstheoreme

$\begin{pmatrix} 0 & \sin(\gamma - \alpha) & \cos(\gamma - \alpha) \\ 0 & \cos(\gamma - \alpha) & -\sin(\gamma - \alpha) \\ -1 & 0 & 0 \end{pmatrix}$

Für β = − π / 2 ergibt die Drehmatrix

$\begin{pmatrix} 0 & -\sin(\gamma + \alpha) & -\cos(\gamma + \alpha) \\ 0 & \cos(\gamma + \alpha) & -\sin(\gamma + \alpha) \\ 1 & 0 & 0 \end{pmatrix}$

In diesen Fällen existieren für α und γ unendlich viele Lösungen.

Berechnung aus Rotationsmatrix

Ist eine Rotationsmatrix gegeben:

$R = \begin{pmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \\ \end{pmatrix}$

Dann können die Winkel folgendermaßen berechnet werden (Craig, S. 47f):

$\beta = \mathrm{Atan2}\left(-r_{31}, \sqrt{ r_{11}^2 + r_{21}^2 } \right)$

$\alpha = \mathrm{Atan2}\left(\frac{r_{21}}{\cos(\beta)}, \frac{r_{11}}{\cos(\beta)}\right)$

$\gamma = \mathrm{Atan2}\left(\frac{r_{32}}{\cos(\beta)}, \frac{r_{33}}{\cos(\beta)}\right)$

Im Falle der oben erwähnten Singularitäten sind folgende Formeln zweckmäßig:

Ist β = π / 2, so setzt man

α = 0

γ = Atan2(r₁₂,r₂₂)

Ist β = − π / 2, so setzt man

α = 0

γ = − Atan2(r₁₂,r₂₂)

Dabei ist Atan2(p,q) die gleichnamige Funktion, die in vielen mathematischen Programmbibliotheken existiert, und die gegenüber der arctan-Funktion oft bevorzugt wird, da sie die sonst nötige Fallunterscheidungen für die vier Quadranten überflüssig macht.

Andere Möglichkeiten, die Orientierung zu beschreiben, sind Rotationsmatrix, Quaternionen oder die Eulerschen Winkel.

Literatur

• John J. Craig: Introduction to Robotics. 2. Auflage. Addison-Wesley Publishing Company, Reading, Mass. [u.a.] 1989, ISBN 0-201-09528-9.