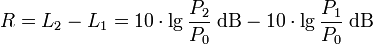Pegel (Physik)

Mit dem Begriff Pegel wird in Nachrichtentechnik, Elektrotechnik und Akustik eine logarithmische Größe bezeichnet, die durch das logarithmierte Verhältnis einer Feld- oder einer Energiegröße zu einem Bezugswert definiert ist. Als Formelzeichen ist L (für level) üblich. Bei Verwendung des dekadischen Logarithmus werden Pegel in der Hilfsmaßeinheit Bel (nach Alexander Graham Bell) bzw. ihrem zehnten Teil, dem Dezibel (Einheitenzeichen dB), bei Verwendung des natürlichen Logarithmus in Neper (Einheitenzeichen Np) angegeben.

Definition, Abgrenzung zum Maß

Als Pegel wird das logarithmierte Verhältnis zweier Leistungsgrößen oder zweier Feldgrößen immer dann bezeichnet, wenn die Größe im Nenner ein fester Bezugswert ist und die gleiche Dimension wie die Zählergröße hat. Zur näheren Bezeichnung des Pegels wird die Zählergröße herangezogen. Beispiel:

$\ L = \lg {P \over P_0}\; \mathrm{B}$.

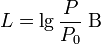ist der Pegel der Leistung bzw. der Leistungspegel bezogen auf den Bezugswert P₀, angegeben in der Hilfsmaßeinheit Bel.

Wegen der handlicheren Zahlenwerte werden im praktischen Gebrauch Pegel nahezu ausnahmslos in Dezibel angegeben. Für das angeführte Beispiel ergibt sich so:

$\ L = 10 \cdot \lg {P \over P_0}\; \mathrm{dB}$.

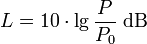Wird von zwei Pegeln mit gleichem Bezugswert die Differenz gebildet, so hängt diese nicht von der Bezugsgröße ab (siehe Rechenregeln für Logarithmen). Für das Beispiel der Differenz von zwei Leistungspegeln ergibt sich:

$\ R = L_2 - L_1 = 10 \cdot \lg {P_2 \over P_0}\; \mathrm{dB} - 10 \cdot \lg {P_1 \over P_0}\; \mathrm{dB}$

$\ R = 10 \cdot \lg {P_2 \over P_1}\; \mathrm{dB}$.

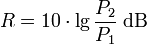Obwohl ebenfalls in Dezibel angegeben, ist die Größe R kein Pegel, sondern ein Maß, da die Größe im Nenner des logarithmierten Verhältnisses kein fester Bezugswert ist^[1][2]. Gelegentlich wird für R auch noch die veraltete und irreführende Bezeichnung "relativer Pegel" verwendet.

Pegel von Feldgrößen und von Leistungsgrößen

Feldgrößen wie die elektrische Spannung oder der elektrische Strom dienen der Beschreibung von physikalischen Feldern. Das Quadrat des Effektivwertes einer solchen Feldgröße ist in linearen Systemen proportional zu dessen energetischem Zustand, der über eine Energiegröße bzw. eine Leistungsgröße erfasst wird. Ohne die genauen Gesetzmäßigkeiten kennen zu müssen, folgt daraus, dass das Verhältnis zweier Energiegrößen gleich dem quadratischen Verhältnis der zugehörigen Effektivwerte der Feldgrößen ist. Für die direkte Berechnung von Pegeln aus Verhältnissen von Effektivwerten von Feldgrößen ergibt sich so ein zusätzlicher Faktor 2, zum Beispiel bei der Berechnung des Spannungspegels L_u aus dem Effektivwert der elektrischen Spannung $\tilde{u}$:

$L_u = 10 \cdot \lg {{\tilde{u}_1}^2 \over {\tilde{u}_0}^2} \; \mathrm{dB} = 20 \cdot \lg {\tilde{u}_1 \over \tilde{u}_0} \; \mathrm{dB}$.

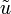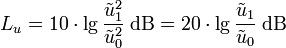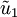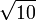Für einen Spannungspegel von 10 Dezibel muss daher die Spannung $\tilde{u}_1$ das $\sqrt{10}$-fache (ca. 3,162-fache) des Bezugswertes 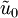$\tilde{u}_0$ sein.

Vorteile der Verwendung von Pegeln

In der Physik bewegen sich Signalamplituden häufig über mehrere Größenordnungen: Beispielsweise Megavolt zu Nanovolt als Verhältnisse von Feldgrößen und Megawatt zu Picowatt als Verhältnisse von Energiegrößen, die in diesem Fall gleichbedeutend mit Leistungsgrößen sind. Durch den Logarithmus sind diese Größen für den praktischen Gebrauch in gut lesbaren meistens zwei- bis dreistelligen Zahlen darstellbar.

Kennlinien von Verstärkern, Filtern oder anderen elektronischen Elementen und Spektren in der Akustik lassen sich einfacher und übersichtlicher darstellen, da das Diagramm wegen der logarithmischen Darstellung eine hohe Dynamik erfasst.

Ein weiterer Vorteil ist die einfache Rechenweise mit logarithmischen Einheiten: Der Ausgangspegel hintereinandergeschalteter Verstärker- oder Dämpfungselemente (z. B. Kabel oder Steckverbindungen) kann durch einfache Addition des Eingangspegels mit den einzelnen logarithmischen Verstärkungs- bzw. Dämpfungswerten erhalten werden.

Anwendung

Pegelangaben sind speziell in der Akustik weit verbreitet. Anwendungen finden sich aber auch in der Hochfrequenztechnik als Teil der Nachrichtentechnik, der Tontechnik (siehe Audiopegel) und der Automatisierungstechnik. Zur speziellen Anwendung bei Spannungen in der Elektrotechnik siehe Spannungspegel.

Bei Pegelangaben hörbarer Schalle werden überwiegend Filter zur Frequenzbewertung benutzt. Diese Filter sollen ein Messergebnis herbeiführen, das mit dem tatsächlichen Lautstärkeeindruck besser zusammenpasst als die unbewertete Angabe. Nach allen Standards der ISO ist eine Frequenzbewertung durch einen Index an der Pegelgröße anzugeben. Abweichend davon werden häufig die folgenden Schreibweisen benutzt, um die Verwendung der unterschiedlichen Bewertungsfilter anzuzeigen.

dB_A, dB(A), „dBA“

dB_B, dB(B), „dBB“

dB_C, dB(C), „dBC“

Rechnen mit Pegeln

Da für Pegelrechnungen die Rechenregeln für Logarithmen gelten, gehen z. B. Multiplikationen der physikalischen Größen in Additionen über.

Für Leistungsgrößen bzw. Energiegrößen wie die Intensität und die Leistung gilt: Da log₁₀10 = 1 und log₁₀2 ≈ 0,3 ist, kann man sich als Faustregel merken: +10 dB bedeutet Verzehnfachung, +3 dB bedeutet Verdopplung, -10 dB bedeutet ein Zehntel, -3 dB die Hälfte. Andere Werte kann man hieraus abschätzen, z. B. +16 dB = (+10+3+3) dB, also: Ursprungswert*10*2*2; +16 dB ist somit das 40-fache.

Für Feldgrößen wie beispielsweise die linearen Schallfeldgrößen, die Spannung und die Stromstärke, gilt die Faustregel: +20 dB entspricht einer Verzehnfachung, -20 dB einem Zehntel; +6 dB bedeutet eine Verdopplung, -6 dB eine Halbierung. Andere Werte kann man hieraus abschätzen; z. B. ergibt sich für eine Dämpfung -26 dB bezogen auf 1 Volt: -20 dB entspricht einem Zehntel; daraus ergibt sich: 0,1 Volt = 100 mV; weitere -6 dB (entsprechend einer Halbierung) bezogen auf diese 100 mV ergeben somit 50 mV.

Siehe auch

• Bezugswert (Akustik)

Literatur

Maue, Jürgen H.; Hoffmann, Heinz; von Lüpke, Arndt: 0 Dezibel plus 0 Dezibel gleich 3 Dezibel, Erich Schmidt Verlag, Berlin, 2003, ISBN 3-503-07470-8

Quellen

1. ↑ DIN 5493-2:1994-9 Logarithmische Größen und Einheiten: Logarithmierte Größenverhältnisse - Maße, Pegel in Neper und Dezibel
2. ↑ DIN IEC 60027-3:2004 Formelzeichen für die Elektrotechnik –- Teil 3: Logarithmische und verwandte Größen und ihre Einheiten

Weblinks

• dB-Berechnungen mit dem jeweiligen Rechner
• dB or not dB (pdf document)