Pentamino

Pentomino (auch Pentamino) ist ein Spiel, bei dem eine Fläche mit Platten so gefüllt werden muss, dass alle 12 Platten verwendet werden, und jedes Quadrat der Fläche belegt ist. Pentamino ist als Solospiel, also für eine Person, angelegt; man kann es aber auch als Spiel für zwei oder mehr Spieler modifizieren. Unter dem Namen Pentominos erschien es als Zweipersonenvariante im Hallmarkverlag.^[1]

Das Wort Pentomino wurde vom Mathematiker Solomon W. Golomb erfunden und wurde erstmals im Jahr 1954 in einem Artikel der Fachzeitschrift American Mathematical Monthly verwendet^[2]. Polyominos als übergeordnete Gruppe wurden erstmals 1957 in Scientific American ausführlich diskutiert.

Gelöste Pentominos

Die Spielsteine

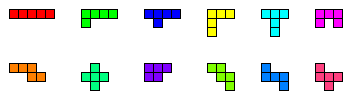
Die 12 Spielsteine sind alle bis auf Symmetrie möglichen Kombinationen, die sich ergeben, wenn man 5 Quadrate so aneinander legt, dass sich die einzelnen Quadrate immer mit der vollen Kante berühren:

Zum besseren Verständnis hat man die Spielsteine mit Buchstaben bezeichnet, die der ungefähren Form des Steins entsprechen. Zeilenweise sind das im Bild: I, L, Y, V, T, U und N, X, P, W, Z, F. Die Spielsteine L, Y, N, P, Z und F liegen in zwei spiegelbildlichen Formen vor, die sich nur zur Deckung bringen lassen, wenn man einen Spielstein wendet. Von den anderen Spielsteinen gibt es nur eine Form, so dass sich insgesamt 18 Formen ergeben.

Als Spiel für eine Person

In diesem Fall ist es ein Geduldspiel. Die Aufgabe besteht darin, aus den 12 Teilen bestimmte Figuren zu legen. Es folgt eine Auswahl an Möglichkeiten:

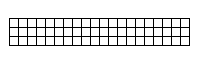
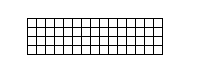
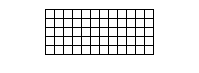
• Rechtecke mit 3x20, 4x15, 5x12 oder 6x10 Feldern:

2 Lösungen	368 Lösungen	1010 Lösungen	2339 Lösungen

• Quadratische Felder mit Aussparungen

• Die größeren 8x8-Varianten (12 Platten):

4340 Lösungen	376 Lösungen	130 Lösungen	42 Lösungen	74 Lösungen

• Die kleineren 7x7-Varianten (9 Platten):

• Felder, die die vergrößerte Form einer einzelnen Platte haben. Dabei besteht dann die Einschränkung, dass man nicht alle 12 sondern nur 9 der 12 möglichen Platten einsetzen kann:

  XXXXXXXXXXXXXXX        XXXXXXXXXXXX        XXXXXXXXX
  XXXXXXXXXXXXXXX        XXXXXXXXXXXX        XXXXXXXXX
  XXXXXXXXXXXXXXX        XXXXXXXXXXXX        XXXXXXXXX
                            XXX              XXX   XXX
                            XXX              XXX   XXX
                            XXX              XXX   XXX

• andere Formen:

    X               X
   XXX             XXX
  XXXXX           XXXXX
 XXXXXXX         XXXXXXX
XXXXXXXXX         XXXXX
                   XXX
                    X

Es gibt noch weitere Geduldspiele wie das Geburtstagspuzzle bei dem auf einem 8x8 Spielfeld 12 Pentamino-Steine so untergebracht werden müssen, dass die 4 freibleibenden Quadrate ein bestimmtes Datum anzeigen.

Als Spiel für zwei Personen

Ein mögliches Regelwerk für ein Strategiespiel mit 2 Personen wäre das folgende:

• Alle Teile werden aufgeteilt, indem abwechselnd jeder Spieler ein Teil an sich nimmt.
• Sind alle Teile vergeben, beginnt das Spiel. Die Spieler legen abwechselnd eines ihrer Pentaminos auf ein vorher gewähltes Spielfeld
• Der Spieler, der zuerst keinen Spielstein mehr auf dem Spielfeld unterbringen kann, hat verloren

Käufliche Mehrpersonenspiele, die mit Pentomino- (bzw. Polyomino-) Steinen arbeiten gibt es mehrere.

Eine (unvollständige) Liste wäre :

• Pentominoes (1973 bei Hallmark erschienen basierend auf den Ideen von Golomb). Die 12 Pentomino-Steine werden abwechselnd auf einem Schachbrett aufgelegt, bis kein Zug mehr möglich ist - der Spieler mit dem letzten Zug gewinnt. Hierzu existiert eine Gewinnstrategie für den Spieler, der beginnt ^[3]
• Blokus (ebene Steine, wohl das bekannteste)
• Duopento (ebene Steine, Regel ähnlich obiger)
• Rumis (3D-Steine)
• Turm-Baumeisterspiel (3D-Steine)
• Ubongo (ebene Steine)

3D Pentaminos

Anstelle von Quadraten kann man die Spielsteine auch aus Würfeln bilden (sie werden dann auch Pentakuben genannt). Aus diesen Spielsteinen können dann, genau wie aus dem Somawürfel, viele verschiedene dreidimensionale Objekte gelegt werden, zum Beispiel Boxen mit den folgenden Abmessungen:

• 5×4×3: 3940 Lösungen
• 6×5×2: 264 Lösungen
• 10×3×2: 12 Lösungen

Außerdem kann man einige der Spielsteine selbst vergrößert bauen. Jeder Würfel im nachzubildenden Stein wird durch einen 2x2x3-Block nachgebaut.

Folgende Spielsteine lassen sich nachbauen: F mit 1, P mit 1082, U mit 10, Z mit 24, T mit 3, V mit 21, N mit 51, Y mit 7 und L mit 99 Lösungen.

Pentamino als Computerspiel

Neben der Form des Spiels zum Anfassen, wurde (und wird) Pentamino oft als Tüftelei am Computer umgesetzt.

Varianten

An Stelle von Platten mit 5 Quadraten gibt es das Spiel auch mit Platten, die aus 6 Quadraten zusammengesetzt sind. Diese Variante heißt Hexamino und hat 35 verschiedene Platten. Heptamino hat 108, und Oktamino 369 verschiedene Platten.

Die aus 4 Quadraten zusammengesetzten 5 verschiedenen Platten des Tetramino haben ihren Eingang in das Computerspiel Tetris gefunden.

Anstelle von Quadraten können auch andere geometrische Figuren gewählt werden: gleichseitige Dreiecke, Sechsecke, Rechtecke, gar Gruppen aus zwei oder mehr verschiedenen Figuren. Man muss die Figuren auch nicht mit der vollen Kante aneinander stoßen lassen, sondern kann sie zum Beispiel um die Hälfte verschieben. Die Variationsmöglichkeiten sind enorm.

Das L-Spiel für zwei Personen ist ebenfalls eine Variante, hier wird allerdings nur mit einer Spielfigur (je Spieler) gespielt.

„Parallel polarisierte“ Pentominos

Eine interessante Variante bilden die so genannten „polarisierten“ Pentominos. Denkt man sich die Ebene von senkrechten bzw. waagerechten (parallelen) „Polarisationsfeldern“ durchzogen, so kann man von den meisten Pentominos jeweils zwei Ausführungen unterscheiden, also praktisch eine „waagerechte“ sowie eine „senkrechte“ Variante. Nur die Pentominos W, X und V sind sozusagen „in sich selbst“ polarisiert und kommen daher nur einfach vor. Selbstverständlich ist bei der Konstruktion von Puzzles nun darauf zu achten, dass die Teile alle ausschließlich in einer „Polarisationsrichtung“ gebraucht werden dürfen. Unter den genannten Voraussetzungen ergeben sich die folgenden 21 Teile:

"Parallel polarisierte Pentominos"

Lösungsbeispiele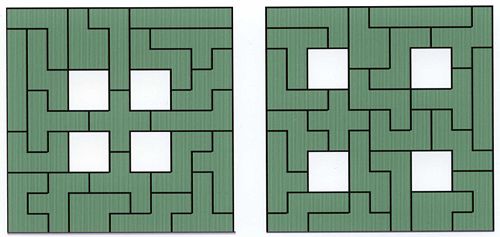

Einzelnachweise

1. ↑ Pentominos in der Spieledatenbank Luding
2. ↑ Die Pentomino-Werkstatt bei Spektrum der Wissenschaft
3. ↑ Hilarie K. Orman: Pentominoes: A First Player Win. In: Richard J. Nowakowski (Hrsg.): Games of no chance: combinatorial games at MSRI, 1994. Cambridge University Press, Cambridge 1996, ISBN 0-521-57411-0

Literatur

• Koth, M. & Grosser, N. (2004). Das Pentomino-Buch. Köln: Aulis Verlag Deubner.
• Blue Balliet, Das Pentomino-Orakel
• Solomon W. Golomb, Polyominoes, 1994, Princeton University Press, ISBN 0-691-02444-8
• Pieter van Delft und Jack Botermanns 'Denkspiele der Welt, 1980, deutsche Ausgabe: München 1977/1980, Hugendubel, ISBN 3-88034-087-0
• Jack Botermanns - Jerry Slocum, Geduldsspiele der Welt, 1986, deutsche Ausgabe: München 1987, Hugendubel, ISBN 3-88034-336-5
• Günter Albrecht-Bühler, Die Pentomino-Werkstatt, Fischer Verlag, Frankfurt 1992 ISBN 3-596-10487-4

Weblinks

• Pentaminos bei mathematische-basteleien.de
• Gerard's Universal Polyomino Solver (englisch)
• Pentominoes (niederländisch, englisch, französisch)