Perfekte Hashfunktion

Eine Perfekte Hash-Funktion ist eine Hash-Funktion 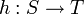$h: S \rightarrow T$, welche unterschiedliche Elemente 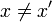$x \neq x'$ aus einer endlichen und festen Schlüsselmenge S auf unterschiedliche Elemente 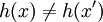$h(x) \neq h(x')$ aus einer Bildmenge T abbildet (keine Kollisionen, Injektivität). Aus der Injektivität folgt ein wichtiger Vorteil: Auf ein Element einer Hashtabelle kann in konstanter Zeit zugegriffen werden.

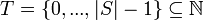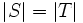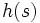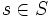Die perfekte Hash-Funktion heißt minimale perfekte Hashfunktion, wenn $T = \{ 0, ..., |S| - 1 \} \subseteq \mathbb{N}\,$, d. h. $|S| = |T|\,$. Das bedeutet, dass die Bildmenge der Funktion h gleichmächtig der Urbildmenge ist. In der Praxis senkt dies den Speicherbedarf des Arrays, welches die Elemente für jedes $h(s)\,$ mit $s \in S\,$ speichert.

Im Gegensatz zu nicht-perfektem Hashing bietet das perfekte Hashing einen Zugriff auf die Elemente in konstanter Zeit 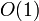$O(1)\,$. Dies wird erreicht, indem die Werte s der Schlüssel in einem von 0 bis |T| - 1 indizierten Array an der Position h(s) gespeichert werden. Im Gegensatz zu normalem Hashing enthält jeder Eimer (Bucket) aufgrund der Injektivität von h also nur genau ein Element. Statt in 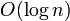$O(\log n)\,$ kann man auf die Elemente dann in konstanter Zeit, also radikal beschleunigt, zugreifen. Dafür bezahlt man mit Rechenzeit um die Hashfunktion h zu konstruieren sowie Speicherplatz für die Speicherung von h.

In der Praxis sucht man Hashfunktionen h mit folgenden Eigenschaften:

• Konstruktion von h in O(n) Zeit, d. h. mit wachsender Schlüsselanzahl |S| steigt die Zeit um h zu konstruieren linear.
• Evaluation von h in O(1), d.h. nach Konstruktion von h kann man einen Schlüssel 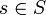$s \in S$ in konstanter Zeit auf einen Index 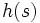$h(s)\,$ abbilden.
• Die Hashfunktion h benötigt möglichst wenig Speicher.
• Die Hashfunktion h soll minimal perfekt sein.

Derzeit gängige perfekte Hashfunktionen arbeiten in 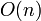$O(n)\,$ Zeit zur Konstruktion von h und benötigen etwa 0,3 mal so viel Speicher wie die Schlüsselmenge S.

(Minimale) perfekte Hashfunktionen sind in der Praxis dann angebracht, wenn:

• Es eine feste Schlüsselmenge S von paarweise verschiedenen Schlüsseln gibt, der jeweils Werte zugeordnet sind (bei sich ständig ändernden Schlüsselmengen wäre eine ständige Neukonstruktion von h zu zeitintensiv)
• Genug Zeit vorhanden ist, um die Hashfunktion h zu konstruieren
• Auf die Werte ein Zugriff in konstanter Zeit benötigt wird
• In konstanter Zeit angefragt werden soll, ob ein Schlüssel in dem Hash vorhanden ist
• Zusätzlicher Speicher für h vorhanden ist

Ein Verfahren zur Konstruktion perfekter Hashfunktionen ist Hash and Displace.