- Photon Antibunching
-
Unter Photon Antibunching versteht man das Nicht-Auftreten von zeitlichen Koinzidenzen einzelner Photonen aus derselben Quelle (siehe Einzelphotonenquelle). Antibunching ist ein rein quantenmechanischer Effekt und tritt bei klassischen Lichtquellen (wie thermischen Lichtquellen und Lasern) nicht auf (speziell bei thermischen Strahlern spricht man dann vom Photon Bunching).
Durch Messung von Antibunching kann der nichtklassische Charakter einer Lichtquelle nachgewiesen werden.
Der Effekt wurde 1977 von Leonard Mandel und seinen Mitarbeitern H. Jeff Kimble, M. Dagenais demonstriert.
Inhaltsverzeichnis
Anschauliche Erklärung
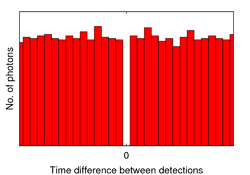
Ein einzelnes Atom mit nur zwei Zuständen stellt eine perfekte Einzelphotonenquelle dar. Die Emission eines Photons erfolgt, wenn das Atom vom angeregten in den Grundzustand übergeht. Bevor ein weiteres Photon emittiert werden kann, muss das Atom zunächst wieder in den angeregten Zustand gelangen (z.B. durch Beleuchten mit resonantem Laserlicht). Zwischen der Emission zweier Photonen desselben Atoms gibt es also immer eine endliche Zeitdifferenz, es können daher nie zwei Photonen gleichzeitig emittiert werden (Antibunching; Bunch ist die englischsprachige Bezeichnung für Teilchenpaket).
Klassische Lichtquellen bestehen hingegen aus makroskopischen Emittern die eine Vielzahl an Atomen enthalten. Diese emittieren unabhängig voneinander Photonen, sodass dort kein Antibunching beobachtet werden kann sondern ganz im Gegenteil die Photonen vermehrt zur gleichen Zeit bei einem Detektor auftreffen (Photon Bunching).
Quantitative Beschreibung
Für einen Fock-Zustand
 mit n Photonen gilt für die Korrelationsfunktion zweiter Ordnung:
mit n Photonen gilt für die Korrelationsfunktion zweiter Ordnung:Perfektes Antibunching (γ(2)(0) = 0) tritt also nur für den Fock-Zustand
 auf.
auf.Auswertung der Korrelationsfunktion
Man misst hierbei die Korrelationsfunktion zweiter Ordnung:
 ,
,
d.i. die Angabe des Erwartungswertes nach einer Zeitspanne τ nach dem Eintreffen eines Photons ein weiteres zu detektieren. Im bisher betrachteten Fall des Einzel-Photonen-Emitters kann man die Intensität über die Erzeugungs- und Vernichtungsoperatoren, die mit den Übergangsoperatoren des Zwei-Niveau-Systems zusammenhängen, ausdrücken, denn es gilt:
 und
und ,
,
sodass wir
erhalten. Für den Fall des Fockn=1-Zustandes erhalten wir speziell:
 ,
,
wobei wir die Eigenschaften der Erzeugungs- und Vernichtungsoperatoren verwendet haben. Einsetzen ergibt:
 .
.
Allgemein gilt für nicht-klassische Zustände: Zum Zeitpunkt der Messung eines ersten Photons (τ = 0) werden weniger Photonen als davor oder danach detektiert. So können diese Zustände identifiziert werden:
 mit
mit  ;[1]
;[1]
dies schließt natürlich den Sonderfall γ(0) = 0 mit ein.
Siehe auch
Einzelnachweise
- ↑ R.Vyas, S. Singh: Antibunching and photoemission waiting times. In: J. Opt. Soc. Am. B. 17, Nr. 4, 2000, S. 634-637. doi:10.1364/JOSAB.17.000634.
Literatur
- Harry Paul: Photonen: Eine Einführung in die Quantenoptik. Vieweg+Teubner Verlag, 1999, ISBN 9783519132226.
- Pierre Meystre, Murray Sargent III: Elements of Quantum Optics. Springer, 2007, ISBN 9783540742098.
Wikimedia Foundation.