Platonischer Monat

Als Zyklus der Präzession oder Platonisches Jahr bezeichnet man die Präzessionsperiode von etwa 25.700 bis 25.800 Jahren. Er wird auch als Das Große Jahr oder Weltjahr erwähnt.

Die Präzessionsdrift der Tierkreiszeichen gegenüber den Sternbildern

Polwanderung: Weg des Himmelsnordpols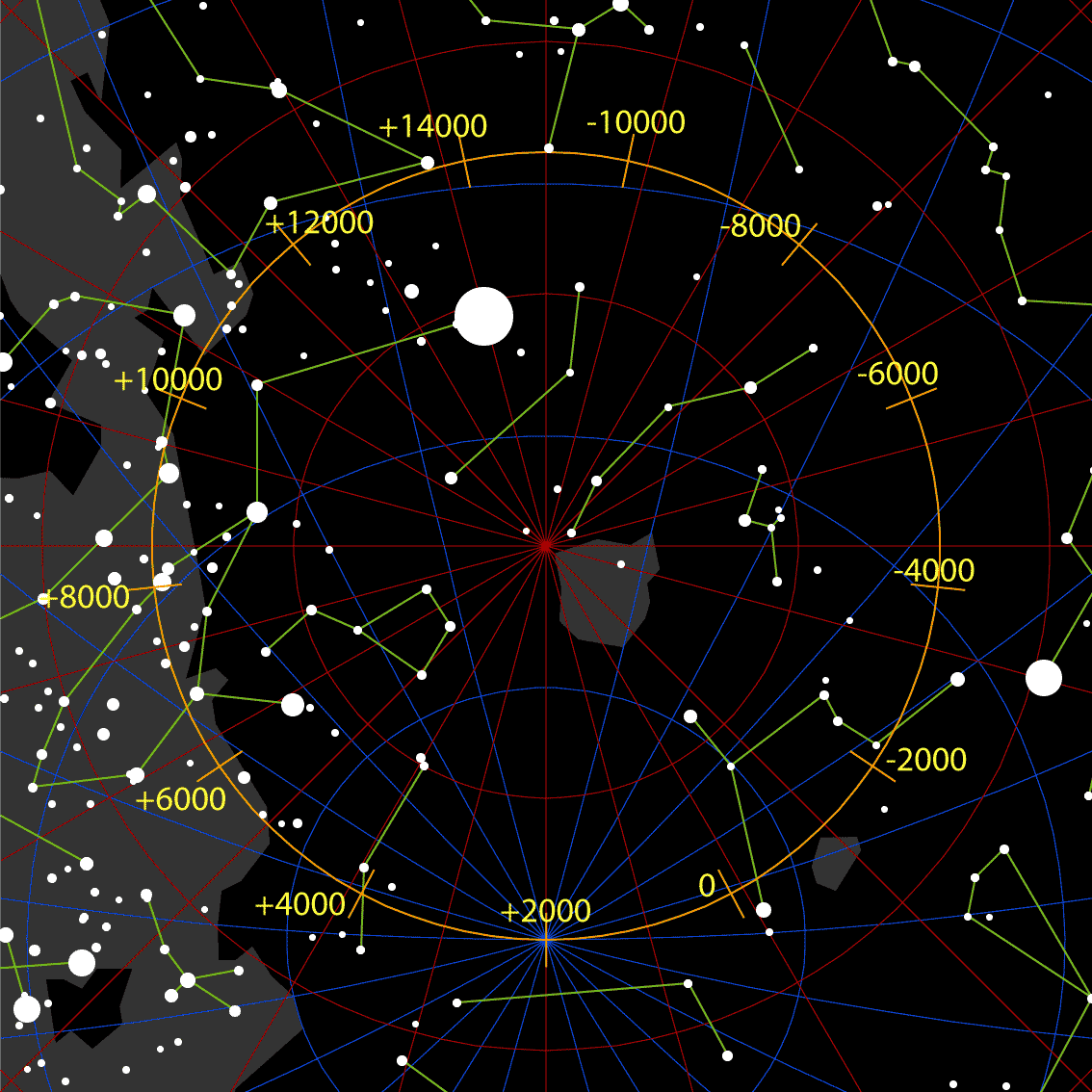

Polwanderung: Weg des Himmelssüdpols

Der Zyklus der Präzession ist die Zeit, nach der man genau ein tropisches Jahr mehr zählt als siderische Jahre. Die Länge dieser beiden Jahre unterliegt – für so lange Zeiträume – trotz prinzipiell exakter Definition solchen Ungenauigkeiten, dass eine exaktere Angabe als auf ein Jahrhundert genau nicht sinnvoll erscheint. (Die zahlreichen Gründe für diesen Sachverhalt sind ausführlich dargelegt in den beiden Artikeln Tropisches Jahr, Siderisches Jahr). Darüber hinaus sind die Geschwindigkeit der Präzession selbst und sogar der Öffnungswinkel des Präzessionskegels (die Schiefe der Ekliptik) über so lange Zeiträume deutlichen Änderungen unterworfen.

Die Drift des Frühlingspunktes korreliert mit der Wanderung des Himmelspols (der Projektion der Erdachse auf die Himmelssphäre): Auf einer Sternkarte präzediert der Frühlingspunkt auf einer Linie normal zur Linie vom Himmelspol zum Ekliptikpol, der sich im Zentrum des Präzessionskreises befindet (Siehe Abbildung).

Die Präzession ist der Grund für das Auseinanderdriften der Sternbilder, die den zwölf Zeichen des Tierkreises den Namen gaben, und der Tierkreiszeichen: Der Frühlingspunkt wird auch als Widderpunkt bezeichnet, nach dem Sternbild Aries (Widder). Er befindet sich zur Zeit aber im westlichen Teil des Sternbildes Pisces (Fische), ist also etwa 25° vom Widder entfernt. So lässt sich das Alter dieser Bezeichnung ungefähr abschätzen. Je nachdem, ob der Punkt ursprünglich den Anfang oder die Mitte des Sternbildes Widder markierte, dürfte er seinen Namen vor grob zwischen 1700 und 3000 Jahren bekommen haben. Leider ist die Quellenlage astronomischer Literatur in der vorarabischen Zeit ziemlich schlecht. Die Präzession an sich dürfte schon den babylonischen Astronomen um 300 v. Chr. bekannt gewesen sein, vielleicht – auf assyrischen Tabellen aufbauend – auch deutlich früher. Da der Grund für die Drift des Frühlingpunktes nicht erkannt wurde (aber auch durch allfällige inkonsistente Übersetzungen), besteht die Möglichkeit, dass die jeweiligen Sternbilder – unter Beibehaltung ihres Names – auf andere Konstellationen übertragen wurden, um sie dem Frühlingspunkt nachzuführen.

Trotz dieser Vorbehalte ist der Zyklus der Präzession eine Methode der Geschichte der Astronomie und Astronomischen Chronologie zur Analyse alter himmelskundlicher Aufzeichnungen. Mittels der Frühlingspunktdrift lässt sich etwa eine erstaunlich frühe Wurzel der chinesischen Kalenderrechnung ^[1] – bis etwa ins 15. Jahrhundert v. Chr. – vermuten oder sich die Tradition der noch immer im Umlauf befindlichen Bauernkalender ^[2] ins ausgehende Mittelalter datieren.

Zwölf Platonische Monate

Das Platonische Jahr wird in zwölf Platonische Monate (Weltmonate, Große Monate auch Weltzeitalter) zu je etwa 2150 Jahren unterteilt. Die Weltmonate tragen die Namen nach den zwölf Tierkreiszeichen. Das Sternbild, in dem sich der Frühlingspunkt zur Zeit befindet, gibt dem Platonsmonat seinen Namen.

Legt man die modernen Grenzen der Sternbilder zu Grunde, so verläuft die Ekliptik allerdings durch dreizehn Sternbilder - nämlich die zwölf Tierkreis-Sternbilder und den Schlangenträger (Ophiuchus). Außerdem nehmen die Sternbilder unterschiedlich große Abschnitte auf der Ekliptik ein. Daher werden die Abschnitte wegen der unterschiedlichen Ausdehnung der Tierkreiszeichen auf 30°-Abschnitte gemittelt, um auf gleichlange Weltmonate zu kommen. Der Abschnitt des Schlangenträger wird dabei dem Skorpion zugeschlagen, um auf zwölf Abschnitte zu kommen. Demnach begann das Fischezeitalter vor knapp 2000 Jahren und endet mit Beginn des Wassermannzeitalters etwa um das Jahr 2200. Allerdings sind die Grenzziehungen relativ willkürlich von unterschiedlichen Herleitungen der Sternbild-Einteilungen abgeleitet: Als Daten, wann nun wirklich das Wassermannzeitalter beginnt, werden Jahreszahlen zwischen 1700 und 2600 genannt.

Die jeweiligen Tierkreiszeichen eines Zeitalters bestimmen nach astrologischer Lehre - neben kurzperiodischeren Schwankungen - einen langfristigen Aspekt, der den Regeln über Wechselwirkungen mit den anderen Aspekten unterliegt.

Tabelle der Termine

Durch die Präzession wandern die Tagundnachtgleichen und die Sonnenwenden einmal durch den gesamten Tierkreis. Legt man gleichabständige Sternbilder, also gleichlange Platonische Monate, sowie eine Periode von 25.800 Jahren zu Grunde, dann ergibt sich folgende Tabelle (Monate gerundet auf halbe Jahrhunderte, Hauptstellungen auf Jahrzehnte):

		30° Sektoren	Eintritt in das Sternbild (unterschiedliche Sektoren)
Sternbild	Sektor	Weltmonat	Frühlingspunkt	Sommerpunkt	Herbstpunkt	Winterpunkt	Dauer
Jungfrau	44,1°	+ 12950 - 12850	+ 12170 - 13630	- 7180	- 730	+ 5720	3160 Jahre
Löwe	35,7°	- 10700	- 10470	- 4020	+ 2430	+ 8880	2570 Jahre
Krebs	20,1°	- 8550	- 7900	- 1450	+ 5000	+ 11450	1440 Jahre
Zwillinge	27,9°	- 6400	- 6460	- 10	+ 6440	+ 12890 -12910	2000 Jahre
Stier	36,7°	- 4250	- 4460	+ 1990	+ 8440	- 10910	2620 Jahre
Widder	24,7°	- 2100	- 1840	+ 4610	+ 11060	- 8290	1770 Jahre
Fische	37,2°	+ 50	- 70	+ 6380	+ 12830 - 12970	- 6520	2670 Jahre
Wassermann	24,0°	+ 2200	+ 2600	+ 9050	- 10300	- 3850	1710 Jahre
Steinbock	28,0°	+ 4350	+ 4310	+ 10760	- 8590	- 2140	2010 Jahre
Schütze	33,3°	+ 6500	+ 6320	+ 12770 - 13030	- 6580	- 130	2380 Jahre
Schlangenträger	18,6°	+ 8650	+ 8700	- 10650	- 4200	+ 2250	1340 Jahre
Skorpion	6,7°		+ 10040	- 9310	- 2860	+ 3590	480 Jahre
Waage	23,0°	+ 10800	+ 10520	- 8830	- 2380	+ 4070	1650 Jahre

- = v. Chr.
+ = n.Chr.

Quellen

1. ↑ Joseph Needham: Wissenschaft und Zivilisation in China. Übers. von Rainer Herbster, Von Colin A. Ronan bearbeitete Ausg., Suhrkamp, Frankfurt am Main, 1984 ISBN 3-518-57692-5
2. ↑ Gottfried Briemle: Der Unterschied zwischen Sternzeichen und Sternbildern. In: Oberösterreichischer Volkskalender 2002. , Verlag Oberösterr. Bauernbund, Linz, S. 71-78