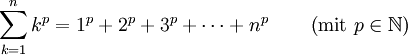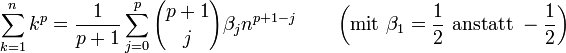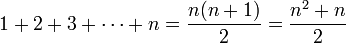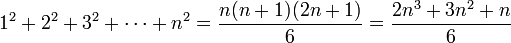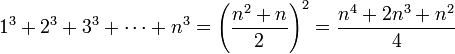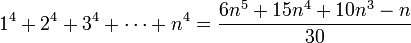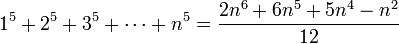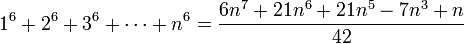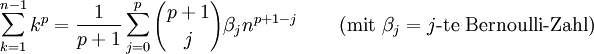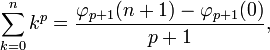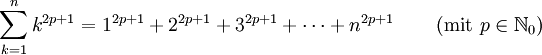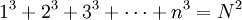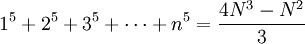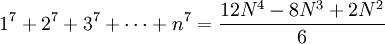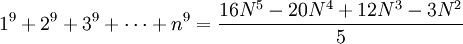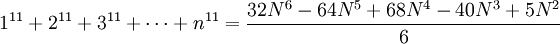Potenzsumme

Die Faulhabersche Formel, benannt nach Johannes Faulhaber, beschreibt, wie sich die Summe der ersten n p-ten Potenzen

$\sum_{k=1}^n k^p = 1^p + 2^p + 3^p + \cdots + n^p \qquad \left(\mbox{mit } p \in \mathbb{N} \right)$

mit einem Polynom in n vom Grad p+1 berechnen lässt. Zur Berechnung der Koeffizienten dieses Polynoms werden die Bernoulli-Zahlen benötigt. Im Folgenden bezeichne β_j die j-te Bernoulli-Zahl, mit der Ausnahme 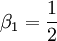$\beta_1=\frac{1}{2}$, dann sieht die Faulhabersche Formel wie folgt aus:

$\sum_{k=1}^n k^p = \frac{1}{p+1} \sum_{j=0}^p {p+1 \choose j} \beta_j n^{p+1-j}\qquad \left(\mbox{mit } \beta_1 = {1 \over 2} \mbox{ anstatt }-{1 \over 2}\right)$

Explizite Berechnung einiger Fälle

$1 + 2 + 3 + \cdots + n = {n(n+1) \over 2} = {n^2 + n \over 2}$

$1^2 + 2^2 + 3^2 + \cdots + n^2 = {n(n+1)(2n+1) \over 6} = {2n^3 + 3n^2 + n \over 6}$

$1^3 + 2^3 + 3^3 + \cdots + n^3 = \left({n^2 + n \over 2}\right)^2 = {n^4 + 2n^3 + n^2 \over 4}$

$1^4 + 2^4 + 3^4 + \cdots + n^4 = {6n^5 + 15n^4 + 10n^3 - n \over 30}$

$1^5 + 2^5 + 3^5 + \cdots + n^5 = {2n^6 + 6n^5 + 5n^4 - n^2 \over 12}$

$1^6 + 2^6 + 3^6 + \cdots + n^6 = {6n^7 + 21n^6 + 21n^5 -7n^3 + n \over 42}$

Eine alternative Darstellung

Wenn man statt den ersten n nur die ersten n-1 Potenzen betrachtet, so kann man die Faulhabersche Formel auch ohne die Ausnahme für β₁ beschreiben und β₁ steht dann für die erste Bernoulli-Zahl:

$\sum_{k=1}^{n-1} k^p = \frac{1}{p+1} \sum_{j=0}^p {p+1 \choose j} \beta_j n^{p+1-j}\qquad \left(\mbox{mit } \beta_j = j\mbox{-te Bernoulli-Zahl}\right)$

Zusammenhang mit Bernoulli-Polynomen

Die Summe der ersten n p-ten Potenzen lässt sich auch mit Hilfe von Bernoulli-Polynomen ausdrücken:

$\sum_{k=0}^{n} k^p = \frac{\varphi_{p+1}(n+1)-\varphi_{p+1}(0)}{p+1},$

Hierbei bezeichnet φ_j das j-te Bernoulli-Polynom.

Faulhaber-Polynome

Die Summen ungerader Potenzen

$\sum_{k=1}^n k^{2p+1} = 1^{2p+1} + 2^{2p+1} + 3^{2p+1} + \cdots + n^{2p+1} \qquad \left(\mbox{mit } p \in \mathbb{N}_0 \right)$

lassen sich auch als Polynom in 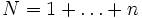$N=1+\ldots+n$ darstellen, solche Polynome in N statt in n werden auch als Faulhaber-Polynome bezeichnet.

Einige Beispiele:

$1^3 + 2^3 + 3^3 + \cdots + n^3 = N^2\,$

$1^5 + 2^5 + 3^5 + \cdots + n^5 = \frac{4N^3 - N^2}{3}$

$1^7 + 2^7 + 3^7 + \cdots + n^7 = \frac{12N^4 -8N^3 + 2N^2}{6}$

$1^9 + 2^9 + 3^9 + \cdots + n^9 = \frac{16N^5 - 20N^4 +12N^3 - 3N^2}{5}$

$1^{11} + 2^{11} + 3^{11} + \cdots + n^{11} = \frac{32N^6 - 64N^5 + 68N^4 - 40N^3 + 5N^2}{ 6}$

Historisches

Johannes Faulhaber selbst kannte die Formel nicht in der hier beschriebenen Form, sondern berechnete lediglich die ungeraden Fälle 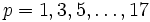$p=1,3,5,\ldots,17$ als Polynom in 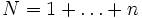$N=1+\ldots+n$ und vermutete, dass für alle ungeraden Zahlen p ein entsprechendes Polynom existiere, ohne jedoch einen Beweis dafür zu haben. Das Konzept der Bernoulli-Zahlen war ihm ebenfalls nicht bekannt. Im Jahre 1834 veröffentlichte Carl Gustav Jacob Jacobi den ersten bekannten Beweis. Weitere Beweise wurden unter anderem von L.Tits (1923) und A.W.F. Edwards (1986) publiziert. Donald Ervin Knuth untersuchte Verallgemeinerungen und trug zur Popularisierung der Faulhaberschen Formel bei.

Literatur

• John H. Conway, Richard Guy: The Book of Numbers. Copernicus, New York 1998, ISBN 0-387-97993-X, S. 107.
• Eric Weisstein: CRC Concise Encyclopedia of Mathematics. Chapman & Hall/CRC, Boca Raton 2003, ISBN 1-58488-347-2, S. 2331.
• Darinnen die miraculosische Inventiones zu den höchsten Cossen weiters „continuirt“ und „profitiert“ werden. In: Johann Faulhaber: Academia Algebrae. Augpurg, bey Johann Ulrich Schöigs, 1631.

Siehe auch

• Euler-Maclaurin-Formel

Weblinks

• Eric W. Weisstein: Faulhaber's formula auf MathWorld (englisch)
• „Johann Faulhaber and Sums of Powers“ von Donald Knuth (englisch)
• Jacobi's Beweis bei MathDoc (lateinisch)
• Faulhaber-Biographie mit Informationen zur Faulhaberschen Formel bei MacTutor