Primal-Dual-Active-Set Algorithmus

Der Primal-Dual-Active-Set-Algorithmus ist ein Verfahren zur Lösung eines quadratischen Optimierungsproblems über einer konvexen Teilmenge S eines Hilbertraumes V über der Menge Ω.

Das Problem

Ein quadratisches Optimierungsproblem ist ein Problem der folgenden Form: Gegeben eine konvexe Menge die durch eine obere Schranke 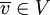$\overline{v} \in V$ beschränkt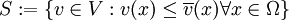

$S := \{ v \in V: v(x) \leq \overline{v}(x) \forall x \in \Omega \}$

ist. Finde 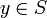$y \in S$ so dass gilt

$y = \text{argmin}_{v \in S} \frac{1}{2}a(v,v) - l(v)$.

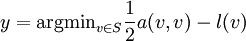Hierbei ist 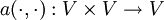$a(\cdot,\cdot):V \times V \rightarrow V$ eine symmetrische stetige Bilinearform und 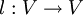$l:V \rightarrow V$ ein stetiger linearer Operator.

Der Algorithmus

Der Primal-Dual-Active-Set-Algorithmus verwendet den Lagrange-Multiplikator λ, um zu einer Lösung zu gelangen, die sowohl erlaubt als auch optimal ist. Der Algorithmus läuft wie folgt ab:

1. Berechnung der aktiven Menge 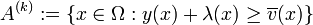$A^{(k)} := \{x \in \Omega: y(x) + \lambda(x) \geq \overline{v}(x)\}$ und der inaktiven Menge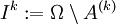 $I^{k} := \Omega \setminus A^{(k)}$
2. Lösung des folgenden Problems

a(y^(k),v) = l(v)inA^(k)

und

$y^{k}(x) = \overline{v}(x) \forall x \in A^{(k)}$

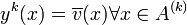
3. Wenn die Lösung nicht die Lagrangebedingungen erfüllt, wird k = k + 1 gesetzt und bei (1) neu begonnen

Anwendungen

Der Primal-Dual-Active-Set-Algorithmus findet insbesondere bei der Lösung von restringierten Problemen über partiellen Differentialgleichungen Anwendung, da die schwache Formulierung einer partiellen Differentialgleichung gerade ein quadratisches Optimierungsproblem ist.

Konvergenzeigenschaften

Durch die Betrachtung des Primal-Dual-Active-Set-Algorithmus als halbglattes Newtonverfahren läßt sich lokal superlineare Konvergenz zeigen.^[1] Für einseitig beschränkte konvexe Teilmengen läßt sich die globale Konvergenz des Primal-Dual-Active-Set-Algorithmus über endlich dimensionalen Hilberträumen zeigen.^[2]

Einzelnachweise

1. ↑ "The primal-dual active set strategy as a semismooth Newton method". M. Hintermuller, K. Ito, K. Kunisch. SIAM J. Optim, 2003.
2. ↑ "A dual-active-set algorithm for positive semi-definite quadratic programming". NL Boland - Mathematical Programming. Springer, 1996.