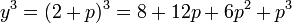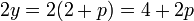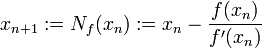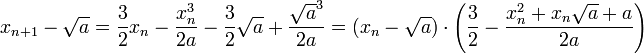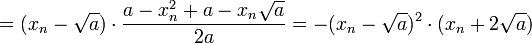- Newtonverfahren
-
Das Newtonsche Näherungsverfahren, auch Newton-Raphsonsche Methode, (benannt nach Sir Isaac Newton 1669 und Joseph Raphson 1690) ist in der Mathematik das Standardverfahren zur numerischen Lösung von nichtlinearen Gleichungen und Gleichungssystemen. Im Falle einer Gleichung mit einer Variablen lassen sich zu einer gegebenen stetig differenzierbaren Funktion
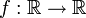 Näherungswerte zu Lösungen der Gleichung f(x) = 0, d. h. Näherungen der Nullstellen dieser Funktion finden. Die grundlegende Idee dieses Verfahrens ist, die Funktion in einem Ausgangspunkt zu linearisieren, d. h. ihre Tangente zu bestimmen, und die Nullstelle der Tangente als verbesserte Näherung der Nullstelle der Funktion zu verwenden. Die erhaltene Näherung dient als Ausgangspunkt für einen weiteren Verbesserungsschritt. Diese Iteration erfolgt bis die Änderung in der Näherungslösung eine festgesetzte Schranke unterschritten hat. Das Iterations-Verfahren konvergiert im günstigsten Fall asymptotisch mit quadratischer Konvergenzordnung, die Zahl der korrekten Dezimalstellen verdoppelt sich dann in jedem Schritt.
Näherungswerte zu Lösungen der Gleichung f(x) = 0, d. h. Näherungen der Nullstellen dieser Funktion finden. Die grundlegende Idee dieses Verfahrens ist, die Funktion in einem Ausgangspunkt zu linearisieren, d. h. ihre Tangente zu bestimmen, und die Nullstelle der Tangente als verbesserte Näherung der Nullstelle der Funktion zu verwenden. Die erhaltene Näherung dient als Ausgangspunkt für einen weiteren Verbesserungsschritt. Diese Iteration erfolgt bis die Änderung in der Näherungslösung eine festgesetzte Schranke unterschritten hat. Das Iterations-Verfahren konvergiert im günstigsten Fall asymptotisch mit quadratischer Konvergenzordnung, die Zahl der korrekten Dezimalstellen verdoppelt sich dann in jedem Schritt.Inhaltsverzeichnis
Newton-Verfahren für reelle Funktionen einer Veränderlichen
Historisches über das Newtonverfahren
Isaac Newton verfasste im Zeitraum 1664 bis 1671 die Arbeit „Methodus fluxionum et serierum infinitarum“ (latein für: Von der Methode der Fluxionen und unendlichen Folgen). Darin erklärt er einen neuen Algorithmus zum Lösen einer polynomialen Gleichung am Beispiel y3 − 2y − 5 = 0. Dazu kann man leicht den Punkt y = 2 als erste Näherung raten. Newton machte den Ansatz y = 2 + p mit einem als „klein“ angenommenen p und setzte diesen in die Gleichung ein:
Nach den binomischen Formeln gilt
-
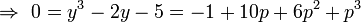 .
.
Da p „klein“ sein soll, können die Terme höherer Ordnung gegen den linearen und konstanten vernachlässigt werden, womit 10p − 1 = 0 bzw. p = 0,1 übrig bleibt. Wir können nun dieses Vorgehen wiederholen und p = 0,1 + q ansetzen, in die zweite Gleichung einsetzen, höhere Terme weglassen und
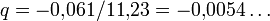 erhalten.
erhalten.Joseph Raphson beschrieb 1690 in der Arbeit „Analysis Aequationum universalis“ diesen Rechenprozess formal und illustrierte den Formalismus an der allgemeinen Gleichung 3. Grades, wobei er die nachfolgende Iterationsvorschrift fand.[1]
Die abstrakte Form des Verfahrens mit Benutzung der Ableitung
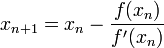 stammt von Thomas Simpson.
stammt von Thomas Simpson.Konstruktion am Graphen
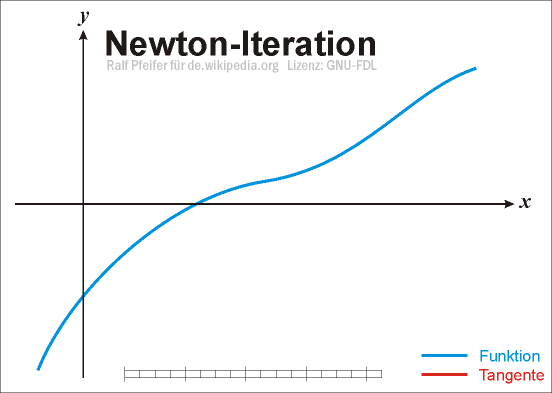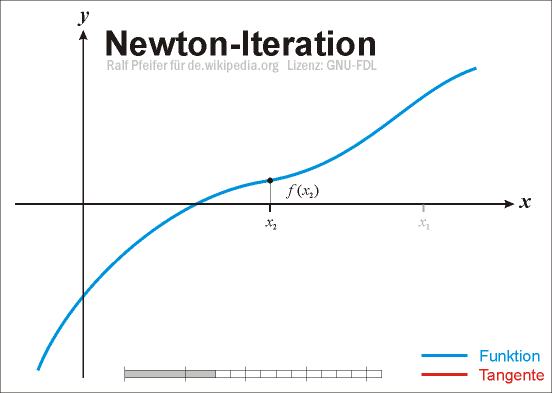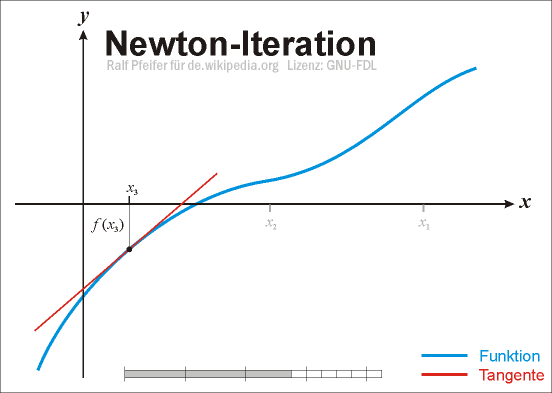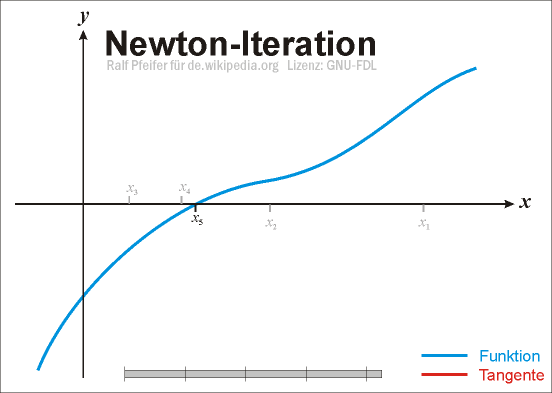
Anschaulich gelangt man wie folgt zu diesem Verfahren: Sei
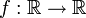 eine stetig differenzierbare reelle Funktion, von der wir eine Stelle xn im Definitionsbereich mit „kleinem“ Funktionswert kennen. Wir wollen einen Punkt xn + 1 nahe xn finden, der eine verbesserte Näherung der Nullstelle darstellt. Dazu linearisieren wir die Funktion f an der Stelle xn, d. h. wir ersetzen sie durch ihre Tangente im Punkt
eine stetig differenzierbare reelle Funktion, von der wir eine Stelle xn im Definitionsbereich mit „kleinem“ Funktionswert kennen. Wir wollen einen Punkt xn + 1 nahe xn finden, der eine verbesserte Näherung der Nullstelle darstellt. Dazu linearisieren wir die Funktion f an der Stelle xn, d. h. wir ersetzen sie durch ihre Tangente im Punkt 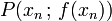 mit Anstieg
mit Anstieg 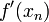 .
.Die Tangente ist durch die Funktion
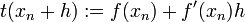 gegeben. Setzen wir h = x − xn ein, so erhalten wir
gegeben. Setzen wir h = x − xn ein, so erhalten wir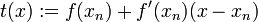 .
.
Wir wählen als xn + 1 die einzige Nullstelle dieser linearen Funktion,
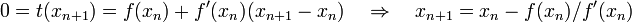 .
.
Wenden wir diese Konstruktion mehrfach an, so erhalten wir aus einer ersten Stelle x0 eine unendliche Folge von Stellen
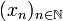 , die durch die Rekursionsvorschrift
, die durch die Rekursionsvorschriftdefiniert ist. Diese Vorschrift wird auch als Newton-Iteration bezeichnet, die Funktion Nf als Newton-Operator. Die Newton-Iteration ist ein spezieller Fall einer Fixpunktiteration, falls die Folge gegen
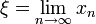 konvergiert, so gilt ξ = Nf(ξ) = ξ − f(ξ) / f'(ξ) und daher f(ξ) = 0.
konvergiert, so gilt ξ = Nf(ξ) = ξ − f(ξ) / f'(ξ) und daher f(ξ) = 0.Die Kunst der Anwendung des Newton-Verfahrens besteht darin, geeignete Startwerte x0 zu finden. Je mehr über die Funktion f bekannt ist, desto kleiner lässt sich die notwendige Menge von Startwerten gestalten.
Viele nichtlineare Gleichungen haben mehrere Lösungen, so hat ein Polynom n-ten Grades bis zu n Nullstellen. Will man alle Nullstellen in einem bestimmten Bereich
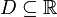 ermitteln, so muss zu jeder Nullstelle ein passender Startwert in D gefunden werden, für den die Newton-Iteration konvergiert. Dazu könnte man z. B. per Bisektion genügend kleine isolierende Intervalle zu jeder Nullstelle bestimmen.
ermitteln, so muss zu jeder Nullstelle ein passender Startwert in D gefunden werden, für den die Newton-Iteration konvergiert. Dazu könnte man z. B. per Bisektion genügend kleine isolierende Intervalle zu jeder Nullstelle bestimmen.Erstes Beispiel
Die Quadratwurzel einer Zahl a > 0 sind die Nullstellen der Funktion f(x) = 1 − a / x2. Diese Funktion hat die Ableitung
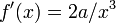 , die Newton-Iteration erfolgt also nach der Vorschrift
, die Newton-Iteration erfolgt also nach der VorschriftDer Vorteil dieser Vorschrift gegenüber dem Wurzelziehen nach Heron (siehe unten) ist, dass es divisionsfrei ist, sobald einmal der Kehrwert von a bestimmt wurde. Als Startwert wurde in der Tabelle x0: = (1 + a) / 2 gewählt. Die Iterierten wurden an der ersten ungenauen Stelle abgeschnitten. Es ist zu erkennen, dass nach wenigen Schritten die Anzahl gültiger Stellen schnell wächst.
n xn bei a = 2 xn bei a = 3 xn bei a = 5 0 1,5 2 3 1 1,40 1,6 1,8 2 1,4141 1,72 2,1 3 1,41421355 1,73203 2,22 4 1,41421356237309502 1,7320508074 2,23601 5 1,414213562373095048801688724209697 1,73205080756887729351 2,236067975 6 1,414213562373095048801688724209698 1,7320508075688772935274463415058723669426 2,236067977499789692 7 1,414213562373095048801688724209698 1,7320508075688772935274463415058723669428 2,23606797749978969640917366873127622 8 1,414213562373095048801688724209698 1,7320508075688772935274463415058723669428 2,23606797749978969640917366873127623 Betrachten wir die Differenz
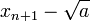 zum Grenzwert im (n + 1)-ten Schritt, so kann mittels der binomischen Formeln die Differenz im n-ten Schritt zweimal abgespalten werden:
zum Grenzwert im (n + 1)-ten Schritt, so kann mittels der binomischen Formeln die Differenz im n-ten Schritt zweimal abgespalten werden:Nach der Ungleichung vom arithmetischen und geometrischen Mittel gilt
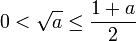 , so dass der zweite Faktor sinnvoll durch 3 / 2(1 + a) beschränkt werden kann. Ist die Differenz im n-ten Schritt eine kleine Zahl, so ist die Differenz im (n + 1)-ten Schritt proportional zum Quadrat davon, also wesentlich kleiner. So entsteht durch Quadrieren eines Fehlers 10 − m eine Fehlerabschätzung proportional zu 10 − 2m. Deshalb spricht man davon, dass sich die Anzahl der gültigen Stellen in jedem Schritt der Newton-Iteration in etwa verdoppelt.
, so dass der zweite Faktor sinnvoll durch 3 / 2(1 + a) beschränkt werden kann. Ist die Differenz im n-ten Schritt eine kleine Zahl, so ist die Differenz im (n + 1)-ten Schritt proportional zum Quadrat davon, also wesentlich kleiner. So entsteht durch Quadrieren eines Fehlers 10 − m eine Fehlerabschätzung proportional zu 10 − 2m. Deshalb spricht man davon, dass sich die Anzahl der gültigen Stellen in jedem Schritt der Newton-Iteration in etwa verdoppelt.Konvergenzbetrachtungen
Das Newton-Verfahren ist ein so genanntes lokal konvergentes Verfahren. Konvergenz der in der Newton-Iteration erzeugten Folge zu einer Nullstelle ist also nur garantiert, wenn der Startwert, d. h. das 0-te Glied der Folge, schon „ausreichend nahe“ an der Nullstelle liegt. Ist der Startwert zu weit weg, kann alles passieren:
- Die Folge divergiert, der Abstand zur Nullstelle wächst über alle Grenzen.
- Die Folge divergiert, bleibt aber beschränkt. Sie kann z. B. periodisch werden, d. h. endlich viele Punkte wechseln sich in immer derselben Reihenfolge ab. Man sagt auch, dass die Folge oszilliert.
- Die Folge konvergiert trotz der Distanz zur Nullstelle, kann jedoch, falls die Funktion mehrere Nullstellen hat, gegen eine andere als die gewünschte Nullstelle (falls man weiß, welche man will) konvergieren.
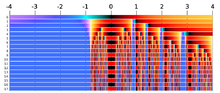 Dynamik des Newton-Verfahrens für die Funktion x3 − 2x + 2 mit Startwerten zwischen −4 und 4: Jede farbcodierte Zeile zeigt das Resultat eines Schritts des Verfahrens, angewandt auf die jeweils darüberliegende Zeile. Die Startwerte befinden sich in der obersten Zeile. Viele Startwerte konvergieren gegen die (einzige reellwertige) Nullstelle des Polynoms bei ca. -1.769, deren Farbe mittelblau ist. Es gibt jedoch auch viele Startwerte, für welche das Verfahren nicht konvergiert und zwischen Null (schwarz) und Eins (rot) hin- und herpendelt. Diese nicht zur Nullstelle führenden Startwerte bilden eine Menge von vollem Maß, bilden also keine Nullmenge, denn sie enthält komplette Intervalle.
Dynamik des Newton-Verfahrens für die Funktion x3 − 2x + 2 mit Startwerten zwischen −4 und 4: Jede farbcodierte Zeile zeigt das Resultat eines Schritts des Verfahrens, angewandt auf die jeweils darüberliegende Zeile. Die Startwerte befinden sich in der obersten Zeile. Viele Startwerte konvergieren gegen die (einzige reellwertige) Nullstelle des Polynoms bei ca. -1.769, deren Farbe mittelblau ist. Es gibt jedoch auch viele Startwerte, für welche das Verfahren nicht konvergiert und zwischen Null (schwarz) und Eins (rot) hin- und herpendelt. Diese nicht zur Nullstelle führenden Startwerte bilden eine Menge von vollem Maß, bilden also keine Nullmenge, denn sie enthält komplette Intervalle.Ist der Startwert
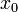 so gewählt, dass das Newton-Verfahren konvergiert, so ist die Konvergenz allerdings quadratisch, also mit der Konvergenzordnung 2 (falls die Ableitung an der Nullstelle nicht verschwindet). Die Menge der Startpunkte, für die das Newton-Verfahren gegen eine bestimmte Nullstelle konvergiert, bildet den Einzugsbereich dieser Nullstelle. Färbt man für eine Polynomfunktion, mit reellen oder komplexen Koeffizienten, die Einzugsbereiche verschiedener Nullstellen in der komplexen Ebene verschieden ein, so ergibt sich ein Newton-Fraktal. In diesem ist zu erkennen, dass die Einzugsbereiche Bassins, d. h. Kreisscheiben um die Nullstellen enthalten, aus welchen heraus die Newton-Iteration stabil gegen die Nullstelle im Zentrum konvergiert. Aber es ist auch zu erkennen, dass die Ränder der Einzugsbereiche „ausgefranst“ sind, sie haben sogar eine fraktale Struktur. Geringe Abweichungen im Startpunkt können also zu verschiedenen Nullstellen führen. Falls es jedoch im Intervall
so gewählt, dass das Newton-Verfahren konvergiert, so ist die Konvergenz allerdings quadratisch, also mit der Konvergenzordnung 2 (falls die Ableitung an der Nullstelle nicht verschwindet). Die Menge der Startpunkte, für die das Newton-Verfahren gegen eine bestimmte Nullstelle konvergiert, bildet den Einzugsbereich dieser Nullstelle. Färbt man für eine Polynomfunktion, mit reellen oder komplexen Koeffizienten, die Einzugsbereiche verschiedener Nullstellen in der komplexen Ebene verschieden ein, so ergibt sich ein Newton-Fraktal. In diesem ist zu erkennen, dass die Einzugsbereiche Bassins, d. h. Kreisscheiben um die Nullstellen enthalten, aus welchen heraus die Newton-Iteration stabil gegen die Nullstelle im Zentrum konvergiert. Aber es ist auch zu erkennen, dass die Ränder der Einzugsbereiche „ausgefranst“ sind, sie haben sogar eine fraktale Struktur. Geringe Abweichungen im Startpunkt können also zu verschiedenen Nullstellen führen. Falls es jedoch im Intervall ![I=]a;b[\,](/pictures/dewiki/98/b0c165bbc3227322c2f565a5cf94d857.png) genau eine Nullstelle gibt, in
genau eine Nullstelle gibt, in 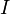 durchweg
durchweg 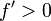 sowie
sowie 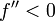 gilt und der Startwert
gilt und der Startwert ![x_0\in I=]a;b[](/pictures/dewiki/54/686a0a6cdd1ecf8ca8e782177ddbeca3.png) links von der Nullstelle
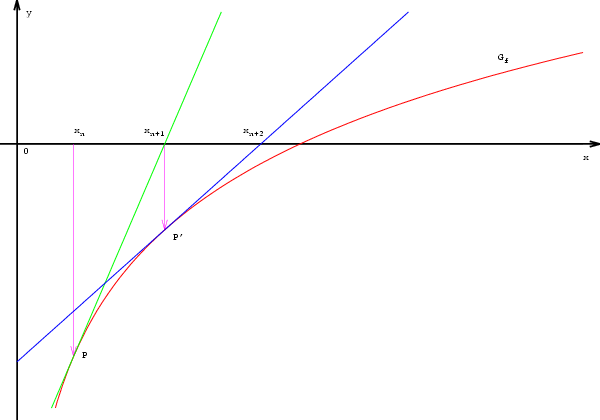
links von der Nullstelle 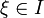 gewählt wird, dann konvergiert die Folge im Newton-Verfahren stets, und zwar streng monoton wachsend (siehe Abbildung unten bzw. die Tabelle oben ab n = 1).
gewählt wird, dann konvergiert die Folge im Newton-Verfahren stets, und zwar streng monoton wachsend (siehe Abbildung unten bzw. die Tabelle oben ab n = 1).Beispiele für Nicht-Konvergenz
- Oszillierendes Verhalten ergibt sich u.a. für das Polynom f(x): = x3 − 2x + 2 [2] mit
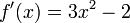 . Der Punkt x = 0 mit f(0) = 2 und
. Der Punkt x = 0 mit f(0) = 2 und 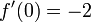 wird durch den Newton-Operator auf den Punkt N(0) = 0 − 2 / ( − 2) = 1 abgebildet, der Punkt x = 1 wiederum, mit f(1) = 1 und
wird durch den Newton-Operator auf den Punkt N(0) = 0 − 2 / ( − 2) = 1 abgebildet, der Punkt x = 1 wiederum, mit f(1) = 1 und 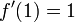 , wird auf N(1) = 1 − 1 / 1 = 0 abgebildet, so dass die Newton-Iteration mit einem dieser Punkte als Startwert eine periodische Folge ergibt, diese beiden Punkte wechseln sich zyklisch ab. Des Weiteren ist dieser Zyklus stabil, er bildet einen Attraktor der Newton-Iteration. Das bedeutet, um beide Punkte gibt es Umgebungen, so dass Startpunkte aus diesen Umgebungen gegen den Zyklus konvergieren und somit je einen der Punkte 0 und 1 als Grenzwert der Teilfolge mit geradem Index und der mit ungeradem Index haben.
, wird auf N(1) = 1 − 1 / 1 = 0 abgebildet, so dass die Newton-Iteration mit einem dieser Punkte als Startwert eine periodische Folge ergibt, diese beiden Punkte wechseln sich zyklisch ab. Des Weiteren ist dieser Zyklus stabil, er bildet einen Attraktor der Newton-Iteration. Das bedeutet, um beide Punkte gibt es Umgebungen, so dass Startpunkte aus diesen Umgebungen gegen den Zyklus konvergieren und somit je einen der Punkte 0 und 1 als Grenzwert der Teilfolge mit geradem Index und der mit ungeradem Index haben. - Divergenz bzw. beliebig weites Entfernen vom Startpunkt ergibt sich für f(x) = sin(x) mit
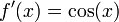 und N(x) = x − tan(x). Es gibt eine Stelle
und N(x) = x − tan(x). Es gibt eine Stelle 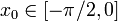 mit tan(x0) = − 2π. Man überzeugt sich, dass dann xn = x0 + 2πn gilt. Dieses Verhalten ist nicht stabil, denn bei leichter Variation des Anfangswertes, wie sie zum Beispiel durch die numerische Berechnung entsteht, entfernt sich die Newton-Iteration immer weiter von der idealen divergierenden Folge. Selbst bei schließlicher Konvergenz wird die gefundene Nullstelle sehr weit vom Startwert entfernt sein.
mit tan(x0) = − 2π. Man überzeugt sich, dass dann xn = x0 + 2πn gilt. Dieses Verhalten ist nicht stabil, denn bei leichter Variation des Anfangswertes, wie sie zum Beispiel durch die numerische Berechnung entsteht, entfernt sich die Newton-Iteration immer weiter von der idealen divergierenden Folge. Selbst bei schließlicher Konvergenz wird die gefundene Nullstelle sehr weit vom Startwert entfernt sein.
Lokale quadratische Konvergenz
Sei f eine zweimal stetig differenzierbare reelle Funktion und a eine Nullstelle von f, in welcher die Ableitung keine Nullstelle hat. Das bedeutet, dass der Graph der Funktion transversal, d. h. nicht-berührend, die x-Achse schneidet. Sei x ein Punkt nahe bei a. Dann kann die Taylor-Formel zweiten Grades (mit Restglied)
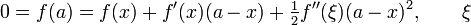 liegt zwischen x und a,
liegt zwischen x und a,
nach der Differenz (x-a) umgestellt werden,
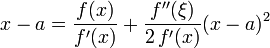 .
.
Es wird nun so umgestellt, dass der Newton-Operator auf der rechten Seite erscheint,
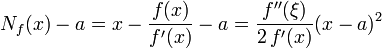 .
.
Seien I ein Intervall um a ohne Nullstelle der Ableitung f'(x) und
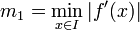 sowie
sowie 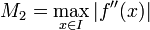 Schranken der Ableitungen von f. Dann folgt für alle
Schranken der Ableitungen von f. Dann folgt für alle 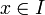 die Abschätzung
die Abschätzung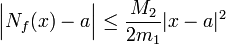 .
.
Mit
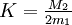 sei der konstante Faktor bezeichnet. In jedem Schritt n der Newtoniteration wird die Größe
sei der konstante Faktor bezeichnet. In jedem Schritt n der Newtoniteration wird die Größe 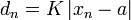 kleiner sein als das Quadrat derselben Größe im vorhergehenden Schritt,
kleiner sein als das Quadrat derselben Größe im vorhergehenden Schritt, 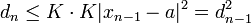 . Nach vollständiger Induktion ergibt sich
. Nach vollständiger Induktion ergibt sich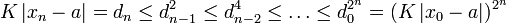 .
.
Kann also für den Startpunkt der Iteration die Abschätzung
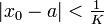 garantiert werden, z. B. indem die Intervallänge von I kleiner als 1/K ist, so konvergiert die Folge (xn) der Newton-Iteration gegen die Nullstelle a, denn die Folge
garantiert werden, z. B. indem die Intervallänge von I kleiner als 1/K ist, so konvergiert die Folge (xn) der Newton-Iteration gegen die Nullstelle a, denn die Folge 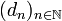 und damit
und damit 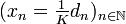 ist nach der angegebenen Abschätzung eine Nullfolge. Die Verkürzung des Intervalls kann durch einige Iterationen eines langsameren Verfahrens zur Nullstelleneinschränkung erreicht werden, z. B. des Bisektionsverfahrens oder der Regula falsi.
ist nach der angegebenen Abschätzung eine Nullfolge. Die Verkürzung des Intervalls kann durch einige Iterationen eines langsameren Verfahrens zur Nullstelleneinschränkung erreicht werden, z. B. des Bisektionsverfahrens oder der Regula falsi.Die aus dieser Abschätzungen folgende Konvergenzgeschwindigkeit wird als quadratisch bezeichnet, die (logarithmische) Genauigkeit bzw. Anzahl gültiger Stellen verdoppelt sich in jedem Schritt. Die Abschätzung des Abstands | xn − a | zur Nullstelle wird oft linear in | x0 − a | angegeben, so gilt z. B.
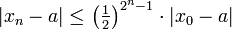 , falls die Länge des Intervalls I kleiner als
, falls die Länge des Intervalls I kleiner als 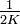 ist. Dies ergibt eine Abschätzung der gültigen Stellen im Binärsystem.
ist. Dies ergibt eine Abschätzung der gültigen Stellen im Binärsystem.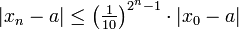 , falls die Länge des Intervalls I kleiner als
, falls die Länge des Intervalls I kleiner als 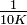 ist, d. h. nahe genug an der Nullstelle ergibt sich eine Verdopplung der gültigen Dezimalstellen in jedem Schritt.
ist, d. h. nahe genug an der Nullstelle ergibt sich eine Verdopplung der gültigen Dezimalstellen in jedem Schritt.
Bemerkungen
- Der lokale Konvergenzbeweis kann auch auf gleiche Weise im mehrdimensionalen Fall geführt werden, allerdings ist er dann technisch etwas schwieriger, da mit zwei- und dreistufigen Tensoren für die erste bzw. zweite Ableitung gearbeitet wird. Im wesentlichen ist die Konstante K durch
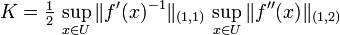 zu ersetzen, mit geeigneten induzierten Operatornormen.
zu ersetzen, mit geeigneten induzierten Operatornormen. - Der lokale Konvergenzbeweis setzt voraus, dass ein eine Nullstelle enthaltendes Intervall bekannt ist. Aus seinem Beweis ergibt sich aber keine Möglichkeit, dies schnell zu testen. Ein Konvergenzbeweis, der auch hierfür ein Kriterium liefert, wurde zuerst von Leonid Kantorowitsch geführt und ist als Satz von Kantorowitsch bekannt.
- Um einen geeigneten Startpunkt zu finden, verwendet man gelegentlich andere („gröbere“) Verfahren. Beispielsweise kann man mit dem Gradientenverfahren eine ungefähre Lösung ermitteln und diese dann mit dem Newton-Verfahren verfeinern.
- Bei unbekanntem Startpunkt kann man mittels einer Homotopie die Funktion f, von der man eine Nullstelle sucht, zu einer einfacheren Funktion g deformieren, von der (mindestens) eine Nullstelle bekannt ist. Man durchläuft dann die Deformation rückwärts in Form einer endlichen Folge sich nur „wenig“ unterscheidender Funktionen. Von der ersten Funktion g kennt man eine Nullstelle. Als Startwert der Newton-Iteration zur gerade aktuellen Funktion der Folge verwendet man die Näherung einer Nullstelle der in der Folge vorhergehenden Funktion. Zum genauen Vorgehen siehe Homotopieverfahren.
-
- Als Beispiel mag die „Flutungshomotopie“ dienen: mit einem willkürlichen z bilden wir die Ausgangsfunktion g(x) = f0(x): = f(x) − f(z) mit bekannter Nullstelle z . Wir haben den „Wasserspiegel“ vom „Nullpegel“ auf die Höhe f(z) geflutet. Nun senken wir schrittweise den Wasserstand,
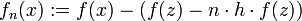 , h = 1 / N,
, h = 1 / N, 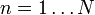 . In jedem Schritt wird eine Näherung ξ(n) einer Nullstelle bestimmt, wobei x0: = ξ(n − 1) gesetzt wird. Es ist fN = f und somit ξ(N) eine der gesuchten Näherungslösungen.
. In jedem Schritt wird eine Näherung ξ(n) einer Nullstelle bestimmt, wobei x0: = ξ(n − 1) gesetzt wird. Es ist fN = f und somit ξ(N) eine der gesuchten Näherungslösungen.
- Als Beispiel mag die „Flutungshomotopie“ dienen: mit einem willkürlichen z bilden wir die Ausgangsfunktion g(x) = f0(x): = f(x) − f(z) mit bekannter Nullstelle z . Wir haben den „Wasserspiegel“ vom „Nullpegel“ auf die Höhe f(z) geflutet. Nun senken wir schrittweise den Wasserstand,
Abbruchkriterien
Mögliche Abbruchkriterien bezüglich einer Restgröße (zum Beispiel Rechner-Arithmetik) sind:
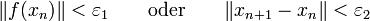
Wobei
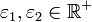 die Qualität der „Nullstelle“ bestimmt. In beiden Fällen kann es vorkommen, dass das Abbruchkriterium zu einem „schlechten“ Zeitpunkt erfüllt ist.
die Qualität der „Nullstelle“ bestimmt. In beiden Fällen kann es vorkommen, dass das Abbruchkriterium zu einem „schlechten“ Zeitpunkt erfüllt ist.Weitere Anwendungsbeispiele
Berechnung der Quadratwurzel
Ein Spezialfall des Newtonschen Näherungsverfahrens ist das Babylonische Wurzelziehen, auch bekannt als Heronverfahren nach Heron von Alexandria:
Wendet man die Iterationsformel zur Nullstellenbestimmung auf die Funktion
- f(x) = x2 − a
an, so erhält man wegen der Ableitungsfunktion f'(x) = 2x für die Lösung
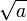 das Näherungsverfahren
das Näherungsverfahren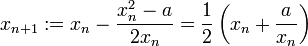 .
.
Dieses Verfahren konvergiert für jedes
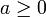 und für jeden beliebigen Anfangswert
und für jeden beliebigen Anfangswert 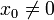 .
.Schnittpunkt zweier Funktionen
Auf ähnliche Weise lässt sich auch der x -Wert des Schnittpunktes zweier Funktionen g(x) und f(x) bestimmen:
Da man die beiden Funktionen zur Lösung des Problems gleichsetzt, lässt sich immer durch Umformung folgende Form, auf die das Newtonsche Näherungsverfahren angewendet werden kann, bestimmen:
- f(x) − g(x) = 0
Trigonometrische Funktion
Gesucht sei die positive Lösung eines Problems x wobei cos(x) = x3. Das Problem kann umformuliert werden als cos(x) − x3 = 0. Gesucht werden also Nullstellen von f(x) = cos(x) − x3.
Wir haben nun f'(x) = − sin(x) − 3x2. Da
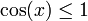 für alle x gilt und x3 > 1 für x > 1, wissen wir, dass die Nullstelle zwischen 0 und 1 liegt. Wir starten die Iteration mit dem Wert x0 = 0,5 .
für alle x gilt und x3 > 1 für x > 1, wissen wir, dass die Nullstelle zwischen 0 und 1 liegt. Wir starten die Iteration mit dem Wert x0 = 0,5 .Damit haben wir die ersten zwölf Ziffern der Nullstelle.
Das folgende Programm in JavaScript bestimmt diese Nullstelle. Um es auszuführen, kopieren Sie den Programmtext inklusive der Marken in eine neue Textdatei und speichern Sie sie mit dem Dateityp .html ab. Öffnen Sie dann die Datei mit einem Webbrowser.
-
Wikimedia Foundation.