- Primscher Algorithmus
-
Der Algorithmus von Prim dient der Berechnung eines minimalen Spannbaumes in einem zusammenhängenden, ungerichteten, kantengewichteten Graphen.
Der Algorithmus wurde 1930 von dem tschechischen Mathematiker Vojtěch Jarník entwickelt. 1957 wurde er zunächst von Robert C. Prim, 1959 von Edsger Dijkstra wiederentdeckt. Daher wird der Algorithmus in der Literatur auch gelegentlich unter anderen Namen geführt, so etwa Prim-Dijkstra-Algorithmus oder Algorithmus von Jarnik, Prim und Dijkstra, im englischen Sprachraum auch Jarniks algorithm oder DJP algorithm.
Inhaltsverzeichnis
Algorithmus
Der Algorithmus beginnt mit einem trivialen Graphen T, der aus einem beliebigen Knoten des gegebenen Graphen besteht. In jedem Schritt wird nun eine Kante mit minimalem Gewicht gesucht, die einen weiteren Knoten mit T verbindet. Diese und der entsprechende Knoten werden zu T hinzugefügt. Das Ganze wird solange wiederholt, bis alle Knoten in T vorhanden sind; dann ist T ein minimaler Spannbaum:
- Wähle einen beliebigen Knoten als Startgraph T.
- Solange T noch nicht alle Knoten enthält:
-
- Wähle eine Kante e minimalen Gewichts aus, die einen noch nicht in T enthaltenen Knoten v mit T verbindet.
- Füge e und v dem Graphen T hinzu.
Der skizzierte Algorithmus wird durch folgenden Pseudocode beschrieben:
G: Graph VG: Knotenmenge von G w: Gewichtsfunktion für Kantenlänge r: Startknoten (r ∈ VG) Q: Prioritätswarteschlange π[u]: Elternknoten von Knoten u im Spannbaum Adj[u]: Adjazenzliste von u (alle Nachbarknoten) wert[u]: Abstand von u zum entstehenden Spannbaum algorithmus_von_prim(G,w,r) 01 Q
 VG //Initialisierung
02 für alle u ∈ Q
03 wert[u]
VG //Initialisierung
02 für alle u ∈ Q
03 wert[u]  ∞
04 π[u]
∞
04 π[u]  0
05 wert[r]
0
05 wert[r]  0
06 solange Q ≠
0
06 solange Q ≠ 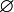 07 u
07 u  extract_min(Q)
08 für alle v ∈ Adj[u]
09 wenn v ∈ Q und w(u,v) < wert[v]
10 dann π[v]
extract_min(Q)
08 für alle v ∈ Adj[u]
09 wenn v ∈ Q und w(u,v) < wert[v]
10 dann π[v]  u
11 wert[v]
u
11 wert[v]  w(u,v)
w(u,v)
Nachdem der Algorithmus endet, ergibt sich der minimale Spannbaum wie folgt:
Beispiel
In diesem Beispiel wird der Ablauf des Algorithmus von Prim an einem einfachen Graphen gezeigt. Der Zwischenbaum T ist jeweils grün hervorgehoben. Alle Knoten, die im jeweiligen Schritt über eine einzelne Kante mit dem Graphen verbunden werden können, sind zusammen mit der jeweiligen Kante geringsten Gewichts blau hervorgehoben. Der Knoten und die Kante, die hinzugefügt werden, sind hellblau markiert.
Vergleich mit dem Algorithmus von Kruskal
Wie auch der Algorithmus von Kruskal, der ebenfalls einen minimal spannenden Baum konstruiert, ist Prims Algorithmus ein Greedy-Algorithmus. Beide Algorithmen beginnen mit einem Graphen ohne Kanten und fügen in jedem Schritt eine Kante mit minimalem Gewicht hinzu. Sie unterscheiden sich vor allem darin, wie die Bildung eines Kreises vermieden wird.
Während Kruskals Algorithmus global nach möglichen besten (d.h. leichtesten) Kanten sucht und bei der Aufnahme dieser Kanten in den Lösungssubgraph die Kreisbildung aktiv vermeidet, betrachtet der Algorithmus von Prim nur Kanten, die von den Knoten der bisher konstruierten Teilknotenmenge zu Knoten der Komplementärmenge verlaufen. Da aus dieser (lokalen) Kantenmenge eine Kante ausgewählt wird, vermeidet der Algorithmus per Konstruktion das Auftreten von Kreisen.
Ein Vergleich der beiden Algorithmen auf Basis der Komplexität ist schwierig, da im Algorithmus von Prim die Knoten die zentrale Komplexitätsschranke bestimmen, während Kruskals Algorithmus auf Basis einer sortierten Kantenliste arbeitet und daher dessen Laufzeit von der Anzahl der Kanten dominiert wird (vergl. dazu etwa E.Horowitz/S.Sahni).
Effiziente Implementierung
Für eine effiziente Implementierung des Algorithmus von Prim muss man möglichst einfach eine Kante finden, die man dem entstehenden Baum T hinzufügen kann. Man benötigt also eine Prioritätswarteschlange (Priority Queue), in der alle Knoten gespeichert sind, die noch nicht zu T gehören. Alle Knoten haben einen Wert, der dem der leichtesten Kante entspricht, durch die der Knoten mit T verbunden werden kann. Existiert keine solche Kante, wird dem Knoten der Wert ∞ zugewiesen. Die Warteschlange liefert nun immer einen Knoten mit dem kleinsten Wert zurück.
Die Effizienz des Algorithmus hängt infolgedessen von der Implementierung der Warteschlange ab. Bei Verwendung eines Fibonacci-Heaps ergibt sich eine optimale Laufzeit von O( | E | + | V | log | V | ). Gemäß der Arbeit Trans-dichotomous Algorithms for Minimum Spanning Trees and Shortest Paths von M.L. Fredman und D.E. Willard (1990) können Minimalgerüste unter Verwendung sogenannter AF-Heaps, die aus Fibonacci-Heaps abgeleitet sind, sogar in Linearzeit O(|V| + |E|) bestimmt werden, wobei |E| quadratisch zu |V| wachsen kann.
Literatur
- R. C. Prim: Shortest connection networks and some generalisations. In: Bell System Technical Journal, 36 (1957), S. 1389–1401
- D. Cherition and R. E. Tarjan: Finding minimum spanning trees. In: SIAM Journal on Computing, 5 (Dez. 1976), S. 724–741
- E. Horowitz and S. Sahni: Fundamentals of Computer Algorithms. In: Computer Science Press, 1978, S. 174–183
Weblinks
Wikimedia Foundation.

![T = \left(V_G, \lbrace\left(u, \pi[u]\right) | u \in V_G \backslash \lbrace r \rbrace\rbrace\right)](/pictures/dewiki/49/140306b643b51ce3859cf8755a296290.png)







